EM算法
1、背景
2、理论
2.1、Jensen不等式
优化理论中,假设 \(f\) 是定义域为实数的函数,如果对于所有的实数 \(x\) ,且二阶导数\(f''(x)\geq 0\) ,则 \(f\) 是凸函数。当 \(x\) 是向量时,如果其Hessian矩阵H是半正定的 (\(H \geq 0\)),那么 \(f\) 是凸函数。且当 \(f''(x)>0\) 或者 \(H>0\) ,那么称 \(f\) 是严格凸函数。
Jensen不等式定义如下:
如果 \(f\) 是任一凸函数,则 \(E\left[f(x)\right]\geq f(\left[x\right])\) 。特别的,如果 \(f\) 是严格的凸函数,那么\(E\left[f(x)\right]=f(\left[x\right])\) 当且仅当 \(p(x=E\left[x\right])=1\) ,即使说 \(x\) 是常量。
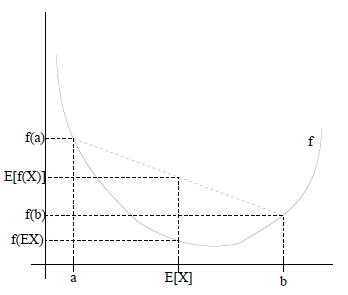
如图所示,实线 \(f\) 是凸函数,\(X\) 是随机变量,分别有 \(0.5\) 的概率位于a或b点(类似于掷骰子)。\(X\) 的期望 \(E\left[X\right]\) 是a和b的均值,从图中可以看到 \(E\left[f(x)\right]\geq f(\left[x\right])\) 成立。
如果 \(f\) 是(严格)凹函数当且仅当 \(-f\) 是严格)凸函数时,其Jensen不等式与凸函数反号,即 \(E\left[f(x)\right]\leq f(\left[x\right])\) 成立。
2.2、EM算法
给定数据样本 \(\left\{x^{1},x^{2},...,x^{m}\right\}\) ,且样本间独立,我们的目的是找到每个样本的隐含类别 \(z\) ,使得概率密度 \(p(x,z)\) 最大。\(p(x,z)\) 的最大似然估计如下:
\[
\begin{align}
l(\theta) &= \sum_{i=1}^{m} log{p(x;\theta)}\\
&= \sum_{i=1}^{m} log{\sum_{z}p(x,z;\theta)}
\end{align}
\]
上式中,第一步是对极大似然函数取对数,第二步是对每个样例可能的类别 \(z\) 求联合概率分布概率的和。因为有隐藏变量 \(z\) 的存在,所以通过上式直接通过最大似然求 \(\theta\) 是比较困难的,但是如果确定 \(z\) 后,求解就比较容易了。
而通过EM算法求解存在隐藏变量 \(z\) 的优化问题比较有效的,其思想是不断地建立 \(l\) 的下界 (E步),然后优化下界 (M步)。具体过程是这样的:
对于每一个样例 \(i\) , \(Q_{i}\) 表示该样例 \(i\) 的隐含变量 \(z\) 的某种分布,\(Q_{i}\) 满足的条件是 \(\sum_{z}Q_{i}(z)=1 ,Q_{i}(z)\geq0\) (如果 \(z\) 是连续的,那么 \(Q_{i}\) 是概率密度函数,需要将求和符号\(\sum\)换成积分符号\(\int\))。比如将教室里学生分类,如果隐藏变量 \(z\) 是身高,那么就是连续的高斯分布,若隐藏变量是性别,那么就是伯努利分布。根据描述内容得到下面的公式:
\[
\begin{align}
\sum_{i}log{p(x^{(i)};\theta})
&=\sum_{i}log\sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta)\\
&=\sum_{i}log\sum_{z^{(i)}}Q_{i}(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}\\
&\geqslant \sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}
\end{align}
\]
上式(3)到(4)比较直接,分子分母同时乘以一个相同的函数 \(Q_{i}(z^{(i)})\) ,从(4)到(5)利用了Jensen不等式,因为 \(log(x)''<0\) ,所以 \(log(x)\) 是凹函数,并且有期望如下,
\[
\begin{align}
\sum_{z^{(i)}} Q_{i}(z^{(i)})
\left[
\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}
\right]
\end{align}
\]
(6)式即为 \(\left[p(x^{(i)},z^{(i)};\theta)/Q_{i}(z^{(i)})\right]\) 的期望。
期望回顾 假设 \(Y\) 是随机变量是 \(X\) 的函数,\(Y=g(X)\)(\(g\) 是连续函数),则:
- \(X\) 是离散型随机变量,它的分布律为 \(P(X=x_{k})=p_{k}\),\(K=1,2,...\) 。若 \(\sum_{k=1}^{+\infty}g(x_{k}p_{k})\) 绝对收敛,则有期望
\[
\begin{align}
E(Y)=E\left[g(X)\right]=\sum_{k=1}^{+\infty}g(x_{k})p_{k}
\end{align}
\]
- \(X\) 是连续型随机变量,它的概率密度为 \(f(x)\),若 \(\int_{-\infty}^{+\infty}g(x)f(x)dx\) 绝对收敛,则有期望
\[
\begin{align}
E(Y)=E[g(X)]=\int_{-\infty}^{+\infty}g(x)f(x)dx
\end{align}
\]
结合上述问题,\(Y\) 是 \(\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}\right]\) ,\(X\) 是 \(z^{(i)}\) ,\(Q_{i}(z^{(i)})\) 是 \(p_{k}\),\(g\) 是 \(z^{(i)}\) 到 \(\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}\right]\) 的映射。这样子解释中的期望,再根据凹函数的Jensen不等式:
\[
\begin{align}
f\left(E_{z^{(i)}\sim{Q_{i}}}\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}\right] \right) \geqslant E_{z^{(i)}\sim{Q_{i}}} \left[f\left(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}\right)\right]
\end{align}
\]
就可以得到式子(5)。
这个过程看作是对 \(l(\theta)\) 求下界。对于 \(Q_{i}\) 的选择有多种可能,但是我们要如何选择最好的?
假设 \(\theta\) 已经给定,那么 \(l(\theta)\) 的值就决定于 \(Q_{i} (z^{(i)})\) 和 \(p(x^{(i)},z^{(i)})\) 了。通过不断调整这两个概率使得下界不断上升,以逼近 \(l(\theta)\) 的真实值,当不等式变成等式的时候,说明我们调整后的概率就能等价于 \(l(\theta)\) 了。按照这个思路,我们就找到等式成立的条件,根据Jensen不等式,要想等式成立,需要让随机变量变成常数值,这里得到:
\[
\begin{align}
\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}=c
\end{align}
\]
上式中 \(c\) 为常数,不依赖于 \(z^{(i)}\) 。对于式子进一步推导,我们知道 \(\sum_{z}Q_{i}(z^{(i)})=1\) ,那么也就有 \(\sum_{z}p(x^{(i)},z^{(i)};\theta)=c\) ,(多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是 \(c\)),那么有下面式子:
\[
\begin{align}
Q_{i}(z^{(i)})
&=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z}p(x^{i},z;\theta)}\\
&=\frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{i};\theta)}\\
&=p(z^{(i)};\theta)
\end{align}
\]
到这里,我们推导出了在固定其他参数 \(\theta\) 后,\( Q_{i}(z^{(i)})\) 的计算公式就是后验概率,解决了\( Q_{i}(z^{(i)})\) 如何选择的问题。这一步就是E步,建立了 \(l(\theta)\) 的下界。接下来是M步,就是在给定\( Q_{i}(z^{(i)})\) 后,调整 \(\theta\) ,去极大化\(l(\theta)\) 的下界 (在固定\( Q_{i}(z^{(i)})\)后,下界还可以调整得更大)。那么一般的EM算法步骤如下:
EM算法 循环重复直到收敛 {
- (E步) 对于每一个 \(i\) ,计算
\[
\begin{align}
Q_{i}(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta)
\end{align}
\]
- (M步) 计算
\[
\begin{align}
\theta :=\arg\max_{\theta} \sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}
\end{align}
\]}
那么如何确保EM收敛?,假定 \(\theta^{(t)}\) 和 \(\theta^{(t+1)}\) 是EM算法第 \(t\) 和 \(t+1\) 次迭代后的结果,如果能够证明 \(l(\theta^{(t)})\leqslant l(\theta^{(t+1)})\) ,也就是说极大似然估计单调递增,那么最终我们会达到最大似然估计的最大值。证明如下:
- 选定 \(\theta^{(t)}\) 后,我们得到E步:
\[
\begin{align}
Q_{i}^{(t)}(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta^{(t)})
\end{align}
\]这一步保证了在给定 \(\theta^{(t)}\) 时,Jensen不等式中的等式成立,即使说
\[
\begin{align}
l(\theta^{(t)})=\sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}
\end{align}
\]
- 然后进行M步,固定 \(Q_{i}^{(t)}(z^{(i)})\) ,并将 \(\theta^{(t)}\) 作为变量,对上面的 \(l(\theta^{(t)})\) 求导后,得到 \(\theta^{(t+1)}\) ,经过一些推导后会有以下公式成立
\[
\begin{align}
l(\theta^{(t+1)})
&\geqslant \sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_{i}(z^{(i)})}\\
& \geqslant \sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_{i}(z^{(i)})}\\
&=l(\theta^{(t)})
\end{align}
\]
公式(18),得到 \(\theta^(t+1)\) 时,只是最大化 \(l(\theta^{(t)})\) ,也就是 \(l(\theta^{(t+1)})\) 的下界,而没有使等式成立,等式成立只有是在固定 \(\theta\) ,并按照E步得到 \(Q_{i}\) 时才能成立,况且,根据我们上面得到的\(l(\theta)
\geqslant \sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)})\times log \times\frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})} \) 对于所有的 \(Q_{i}\) 和 \(\theta\) 都成立;公式11.2利用了M步的定义,即是将 \(\theta^{(t)}\) 调整到 \(\theta^{(t+1)}\) ,使下界最大化,因此(19)成立,(20)是前面的结果。
- 这样就证明了 \(l^{(\theta)}\) 会单调增加。一种收敛方法是 \(l^{(\theta)}\)不再变化,还有一种情况是变化幅度很小。
再次解释一下M。首先(18)对所有的参数都满足,而其等式成立条件只是在固定 \(\theta\),并调整好 \(Q\) 时成立,而第(18)步只是固定 \(Q\),调整 \(\theta\) ,不能保证等式一定成立。(18)到(19)就是M步的定义,(19)到(20)是前面E步所保证等式成立条件。也就是说E步会将下界拉到与 \(l(\theta)\) 一个特定值(这里 \(\theta^{(t)}\))一样的高度,而此时发现下界仍然可以上升,因此经过M步后,下界又被拉升,但达不到与另 \(l(\theta)\) 外一个特定值一样的高度,之后E步又将下界拉到与这个特定值一样的高度,重复下去,直到最大值。
如果我们定义
\[
\begin{align}
J(Q,\theta)=\sum_{i}\sum_{z^{(i)}}Q_{i}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_{i}(z^{(i)})}
\end{align}
\]
从前面的推导中我们知道 \(l(\theta) \geqslant J(Q,\theta)\) ,EM可以看作是 \(J\) 的坐标上升法,E步固定 \(\theta\) ,优化 \(Q\) ,M步固定 \(Q\) 优化 \(\theta\) 。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号