非确定的自动机NFA确定化为DFA

1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} )，其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3}

   画出状态转换矩阵,状态转换图，并说明该NFA识别的是什么样的语言。

 答：

状态转换矩阵，如下

状态\符号	a	b
0	0,1	0
1		2
2		3

状态转换图，如下

 

 

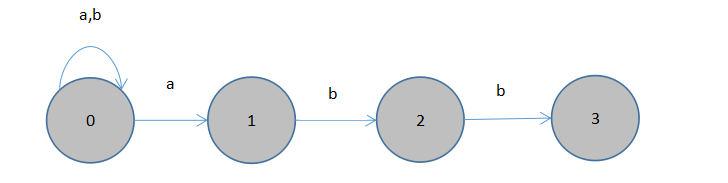
该NFA识别的语言是L(M)=(a|b)*abb

 

2.NFA 确定化为 DFA

1.解决多值映射：子集法

1）. 上述练习1的NFA

答：练习1的NFA 确定化为 DFA的状态转换矩阵，如下

状态\符号	a	b
0	0,1
0,1	0,1	0,2
0,2	0,1	0,3
0,3	0,1	0

状态转换图，如下

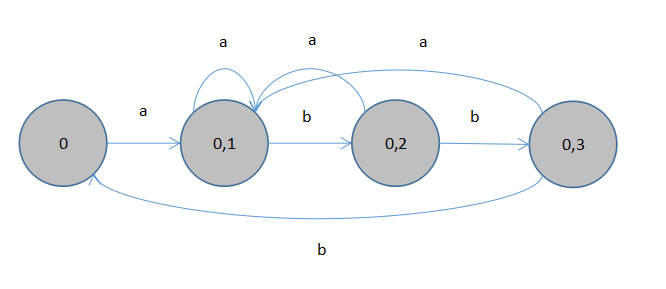
2）. P64页练习3

 

 

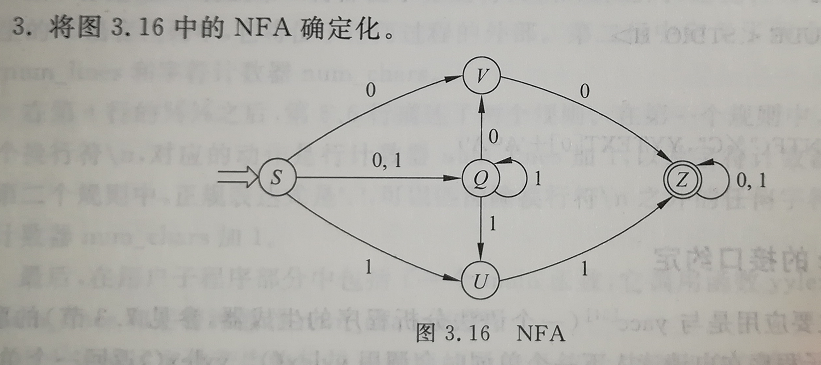
答：

 NFA的状态转换矩阵，如下

状态\符号	0	1
S	V,Q	U
V	Z
Q	V	Q,U
U		Z
Z	Z	Z

 

NFA 确定化为 DFA的状态转换矩阵，如下

名称	状态\符号	0	1
a	S	VQ	Q,U
b	VQ	V,Z	Q,U
c	V,Z	Z	Z
d	Q,U	V	Q,U,Z
e	Q,U,Z	V,Z	Q,U,Z
f	V	Z
g	Z	Z	Z

状态转换图，如下

 

 

 

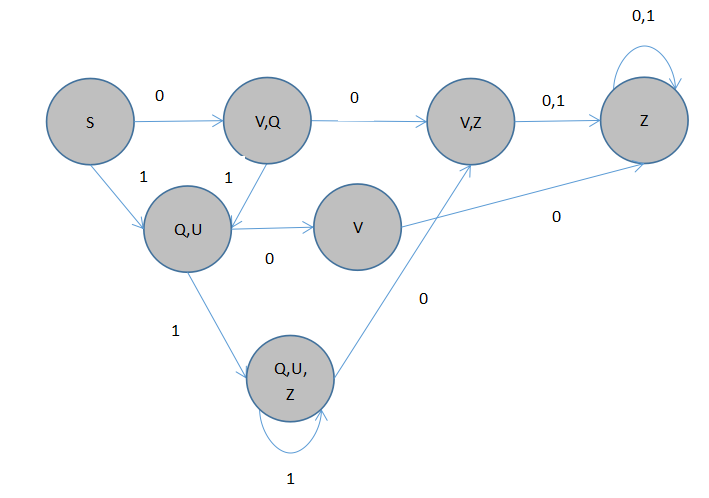
2.解决空弧：对初态和所有新状态求ε－闭包

1）. 发给大家的图2

图2：

 

 

 

 

 

 

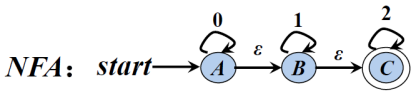
 答：此图一共构造了三个子集分别如下

代表名称	子集
a	{A,B,C}
b	{B,C}
c	{C}

由上表可得：

S={[a],[b],[c]}

∑={0，1，2}

D([a],0)=[a]

D([a],1)=[b]

D([a],2)=[c]

D([b],1)=[b]

D([b],2)=[c]

D([c],2)=[c]

状态转换图，如下

 

 

 

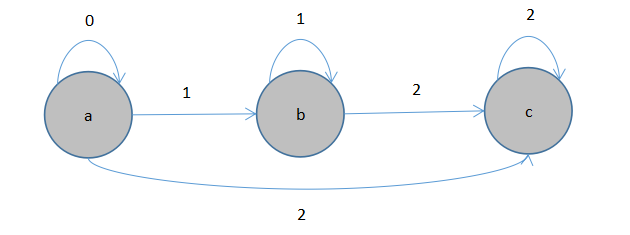
2）.P50图3.6

 

 

 

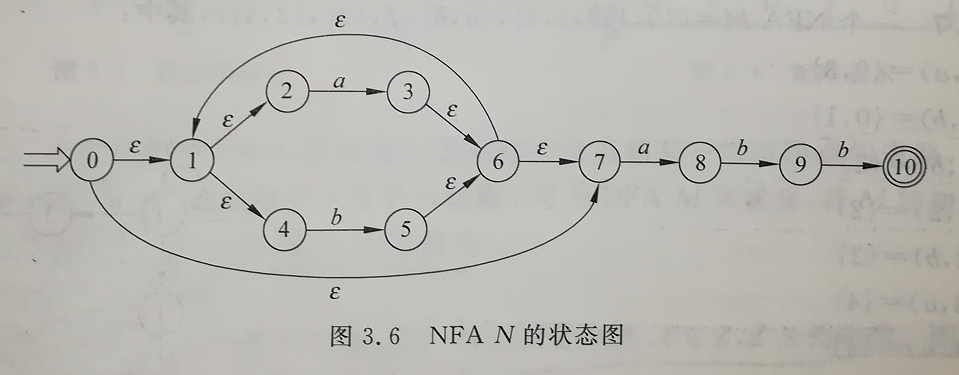
 答：{0,1,2,4,7}中的任一状态都是从状态0经任意条ε弧可到达的状态,令{0,1,2,4,7}=A,则move(A, a)={3,8},因为在状态0,1,2,4和7中,只有状态2和7有a弧射出,分别达到状态3和8

所以有ε-closure({3,8})={3,6,1,2,4,7,8},以此类推可下表（以下ε-closure({3,8})简写为ε{3,8}）

 

状态名称	状态\符号	a	b
0	ε(0)={0,1,2,4,7}	ε{3,8}={3,6,1,2,4,7,8}	ε{5}={5,6,1,2,4,7}
1	ε{3,8}={3,6,1,2,4,7,8}	ε{3,8}={3,6,1,2,4,7,8}	ε{5,9}={5,6,1,2,4,7,9}
2	ε{5}={5,6,1,2,4,7}	ε{3,8}={3,6,1,2,4,7,8}	ε{5}={5,6,1,2,4,7}
3	ε{5,9}={5,6,1,2,4,7,9}	ε{3,8}={3,6,1,2,4,7,8}	ε{5,10}={5,6,1,2,4,7,10}
4	ε{5,10}={5,6,1,2,4,7,10}	ε{3,8}={3,6,1,2,4,7,8}	ε{5}={5,6,1,2,4,7}

状态转换图，如下

 

 

 

 

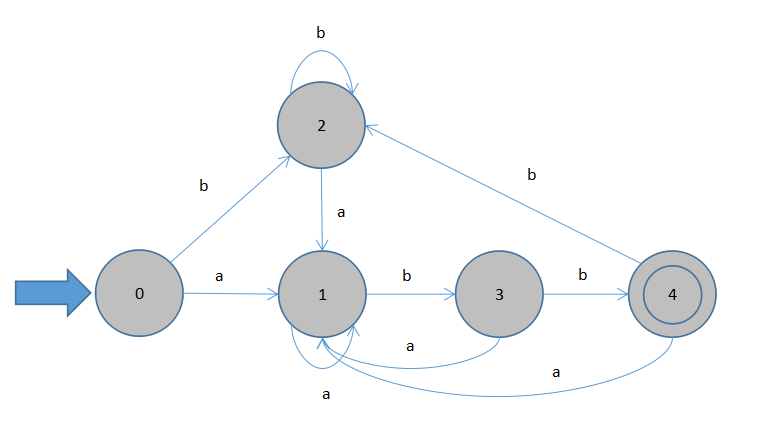
子集法注解：

f(q,a)={q1,q2,…,qn},状态集的子集

将{q1,q2,…,qn}看做一个状态A，去记录NFA读入输入符号之后可能达到的所有状态的集合。

步骤：

1）.根据NFA构造DFA状态转换矩阵

①确定DFA的字母表，初态（NFA的所有初态集）

②从初态出发，经字母表到达的状态集看成一个新状态

③将新状态添加到DFA状态集

④重复23步骤，直到没有新的DFA状态

2）.画出DFA

3）.看NFA和DFA识别的符号串是否一致。