TensorFlow的基本应用

TensorFlow的几个关键词：

图（graph）、会话、张量（tensor）、变量（Variable）、feed、fetch。

关键词的作用：

用图（graph）来表示计算任务
在被称之为会话（Session）的上下文（context）中执行图
使用tensor表示数据
通过变量（Variable）维护状态
用feed和fetch可以为任意操作赋值或者从中获取数据

Tensorflow中用图来表示计算任务，图中的每个节点我们叫它OP，并且每一个OP都可以获得0个以上的tensor，然后执行计算后产生0个或多个tensor；而在计算图的时候为了能够进行计算，必须在会话（session）中启动图，session会将图上的OP分配到CPU、GPU等设备上（我们无需具体的定义使用CPU还是GPU，如果检测到GPU，TensorFlow会用检测到的第一个GPU来执行），同时提供执行OP的方法，执行完成后再将OP返回。

变量用来维护图执行过程中的状态信息，例如在神经网络总用于保存和更新神经网络上的参数。

Feed主要用于临时替换一个操作的输出结果，我们可以提供feed数据作为run()函数调用的参数，feed只在方法内有效，结束后feed就会消失，常见的一种形式是我们用tf.placeholder()来创建占位符，方便于feed在run()内的赋值。

实验：

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt

print(tf.__version__)

fashion_mnist = keras.datasets.fashion_mnist

(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()

class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

train_images.shape
len(train_labels)
train_labels
test_images.shape
len(test_labels)

plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()

train_images = train_images / 255.0

test_images = test_images / 255.0

plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()

model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10)
])

model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])

model.fit(train_images, train_labels, epochs=10)

test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)

print('\nTest accuracy:', test_acc)

probability_model = tf.keras.Sequential([model,
tf.keras.layers.Softmax()])
predictions = probability_model.predict(test_images)
predictions[0]
np.argmax(predictions[0])
test_labels[0]

def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array, true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])

plt.imshow(img, cmap=plt.cm.binary)

predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'

plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)

def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)

thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')

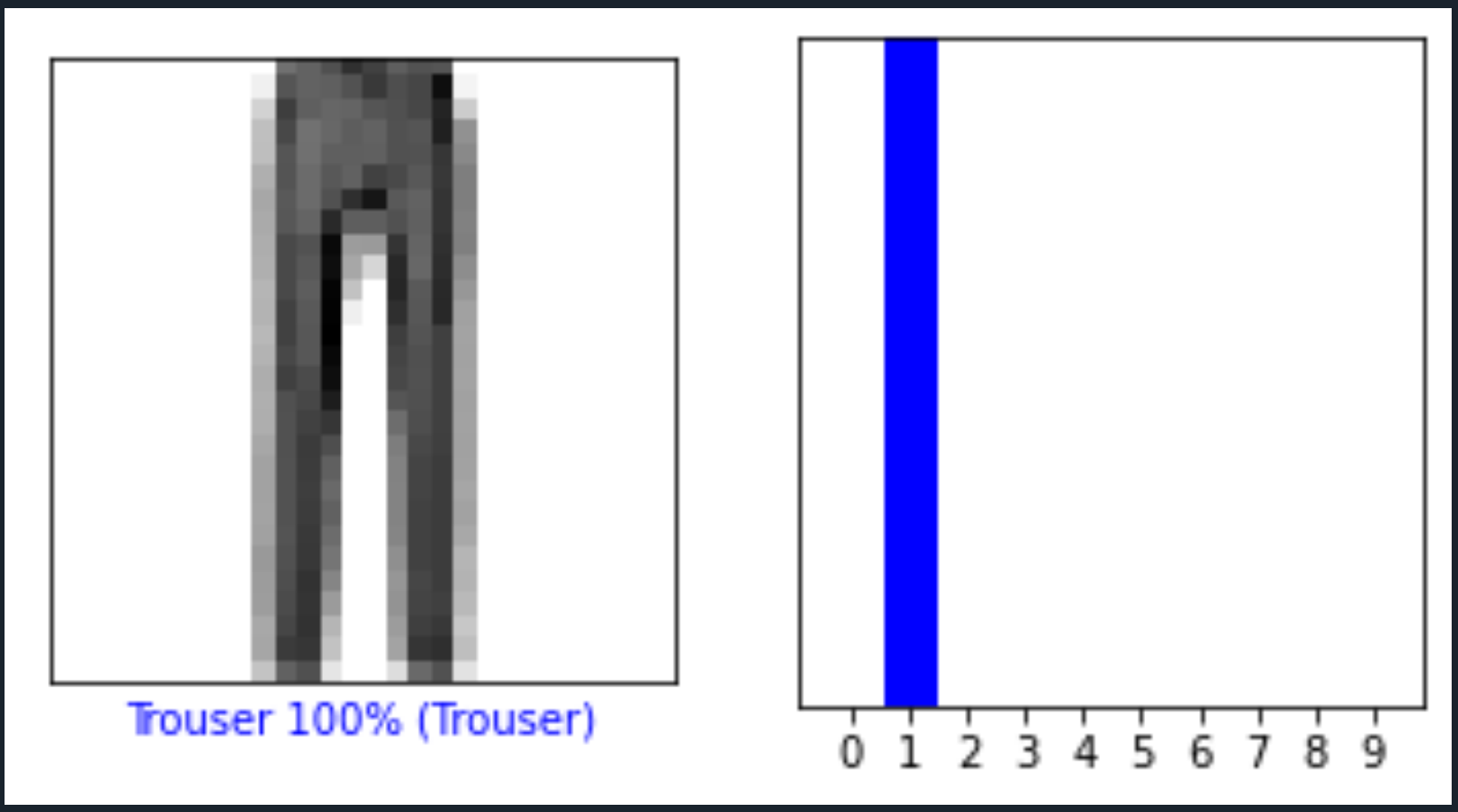
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], test_labels)
plt.show()

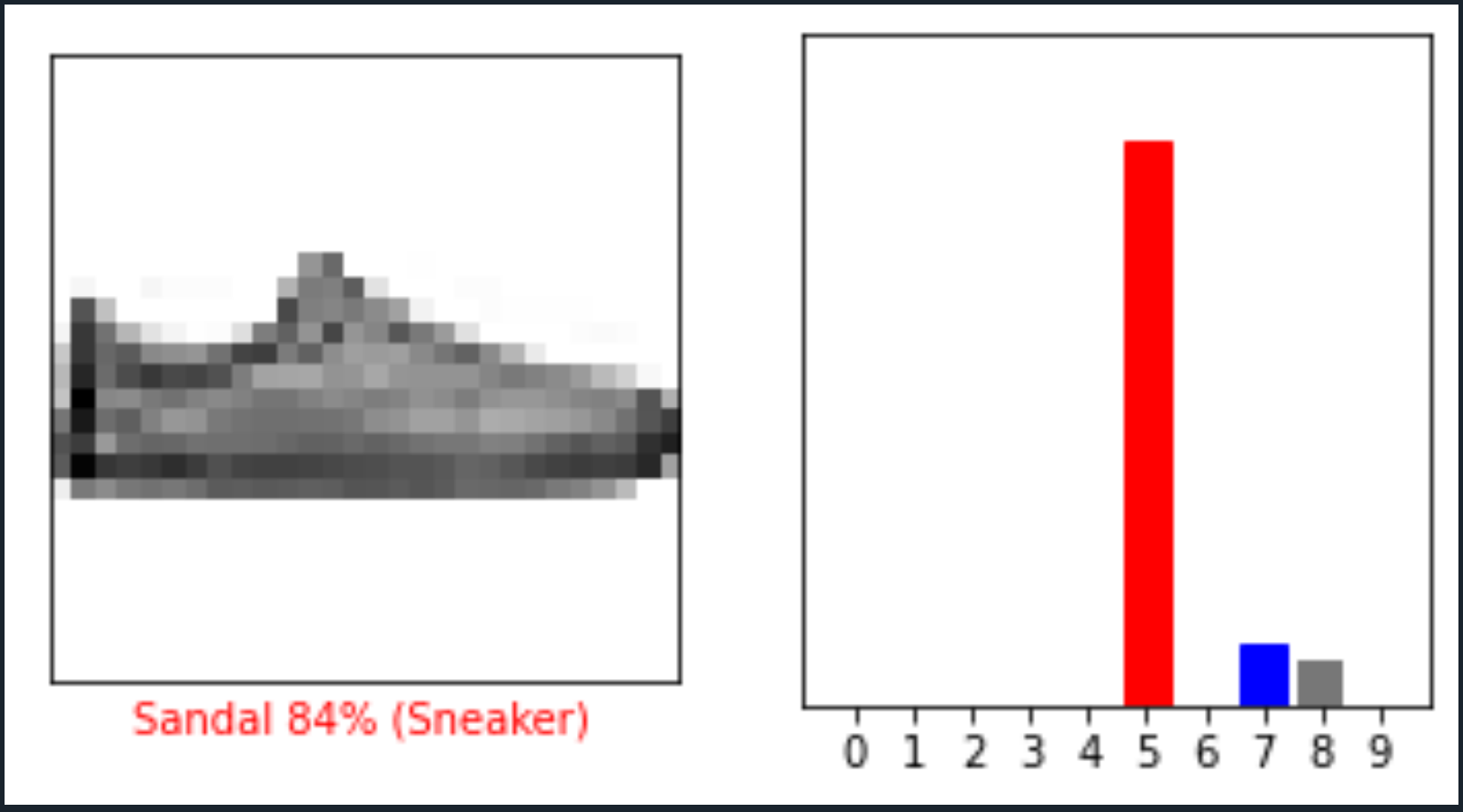
i = 12
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], test_labels)
plt.show()

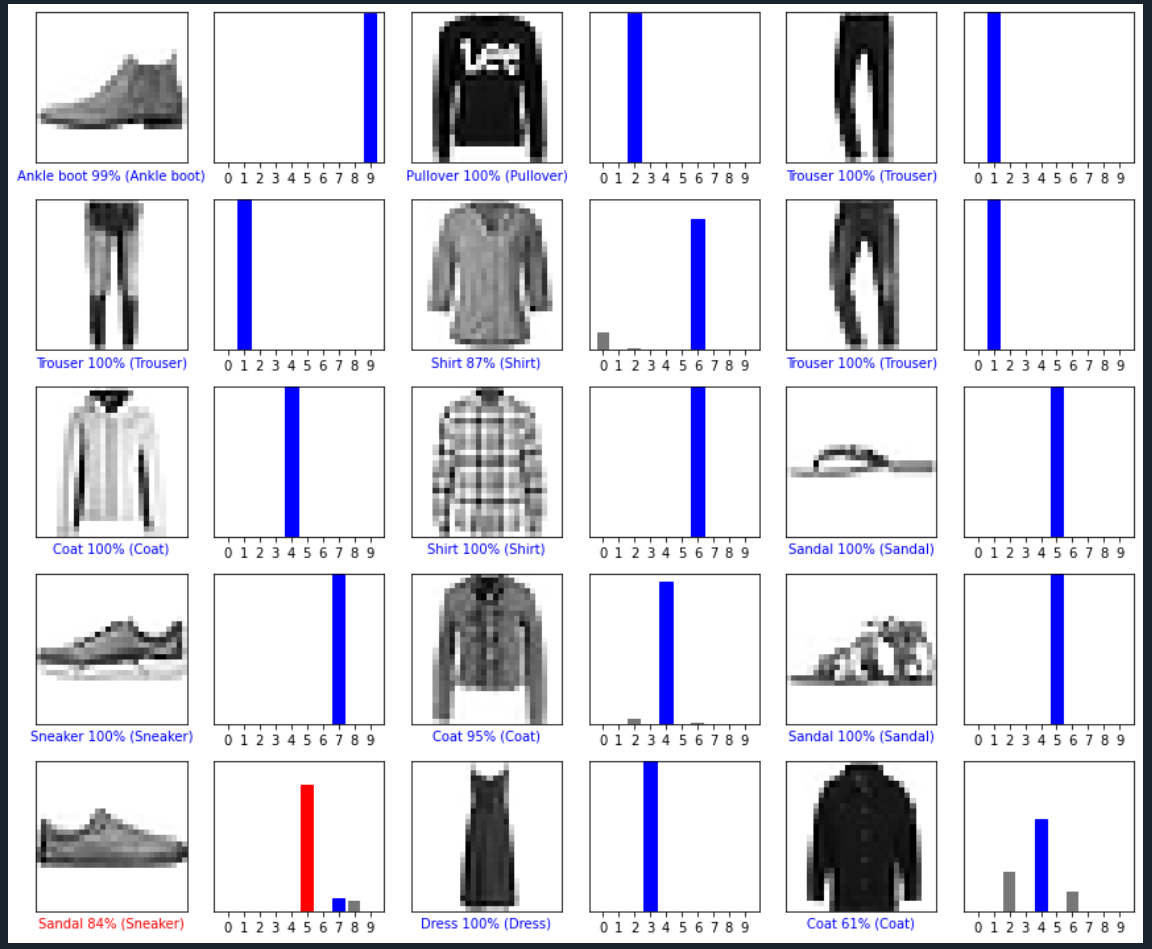
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions[i], test_labels)
plt.tight_layout()
plt.show()

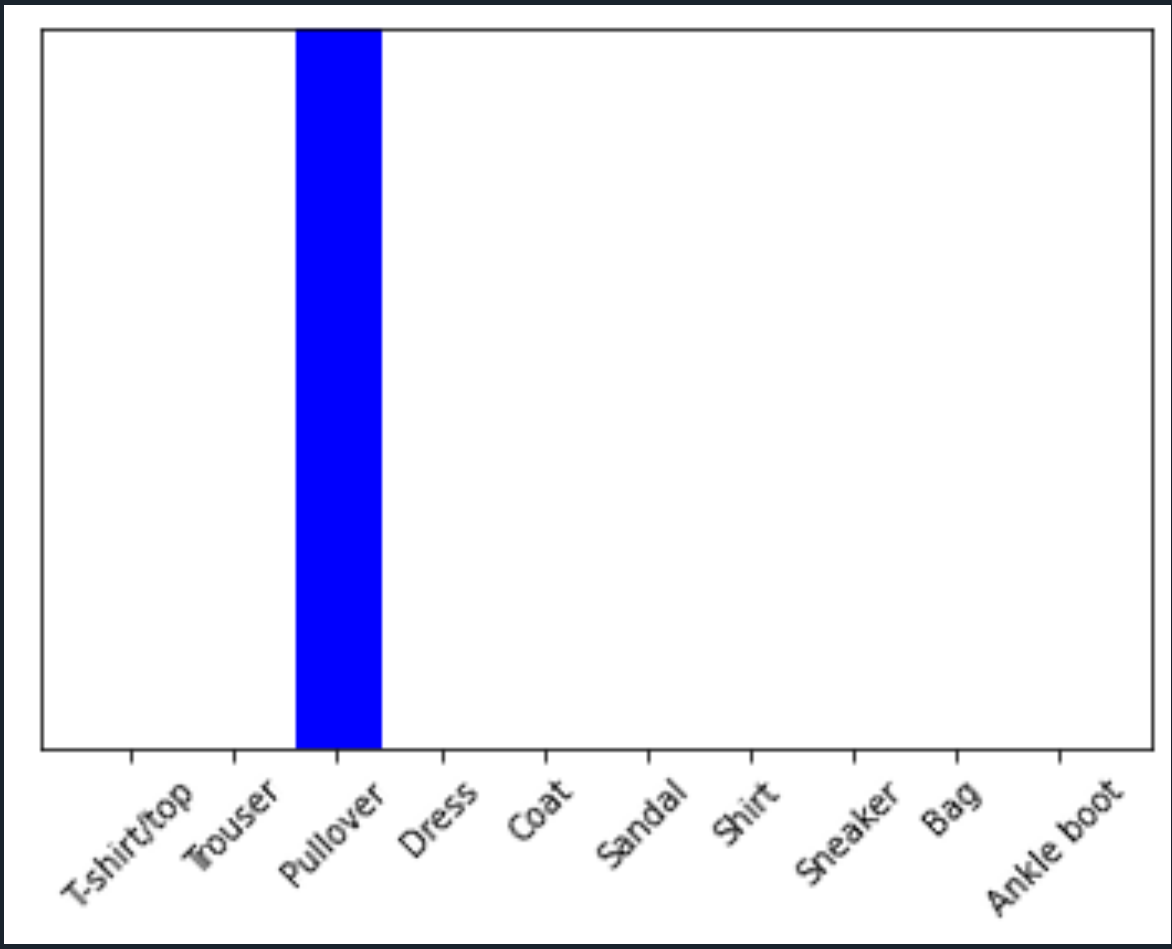
img = test_images[1]

print(img.shape)

img = (np.expand_dims(img,0))

print(img.shape)

predictions_single = probability_model.predict(img)

print(predictions_single)

plot_value_array(1, predictions_single[0], test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)

np.argmax(predictions_single[0])

结果：

课后习题：

（1）：

       卷积中的局部连接：层间神经只有局部范围内的连接，在这个范围内采用全连接的方式，超过这个范围的神经元则没有连接；连接与连接之间独立参数，相比于去全连接减少了感受域外的连接，有效减少参数规模。

        全连接：层间神经元完全连接，每个输出神经元可以获取到所有神经元的信息，有利于信息汇总，常置于网络末尾；连接与连接之间独立参数，大量的连接大大增加模型的参数规模。

（2）：

        利用快速傅里叶变换把图片和卷积核变换到频域，频域把两者相乘，把结果利用傅里叶逆变换得到特征图。

（3）：

        池化操作的作用：对输入的特征图进行压缩,一方面使特征图变小,简化网络计算复杂度;一方面进行特征压缩,提取主要特征。

        激活函数的作用：用来加入非线性因素的，解决线性模型所不能解决的问题。

（4）：

        消除数据之间的量纲差异，便于数据利用与快速计算。

（5）：

        寻找损失函数的最低点，就像我们在山谷里行走，希望找到山谷里最低的地方。那么如何寻找损失函数的最低点呢？在这里，我们使用了微积分里导数，通过求出函数导数的值，从而找到函数下降的方向或者是最低点（极值点）。损失函数里一般有两种参数，一种是控制输入信号量的权重(Weight, 简称  ），另一种是调整函数与真实值距离的偏差（Bias，简称  ）。我们所要做的工作，就是通过梯度下降方法，不断地调整权重  和偏差b，使得损失函数的值变得越来越小。而随机梯度下降算法只随机抽取一个样本进行梯度计算。