吴恩达深度学习笔记-12（特殊应用）

目录

• 特殊应用
  • 人脸识别
  • One-Shot learning
  • Siamese网络
  • 三元组损失
  • 面部识别与二分类问题的联系

特殊应用

人脸识别

首先简单介绍一下人脸验证（face verification）和人脸识别（face recognition）的区别。

• 人脸验证：输入一张人脸图片，验证输出与模板是否为同一人，即一对一问题。

• 人脸识别：输入一张人脸图片，验证输出是否为K个模板中的某一个，即一对多问题。
  一般地，人脸识别比人脸验证更难一些。因为假设人脸验证系统的错误率是1%，那么在人脸识别中，输出分别与K个模板都进行比较，则相应的错误率就会增加，约K%。模板个数越多，错误率越大一些。

One-Shot learning

One-shot learning只使用一个训练样例，或者说只提供一张某人的照片，使得算法能够识别此人。

但是One-shot learning的性能并不好，其包含了两个缺点：

• 每个人只有一张图片，训练样本少，构建的CNN网络不够健壮。
• 若数据库增加另一个人，输出层softmax的维度就要发生变化，相当于要重新构建CNN网络，使模型计算量大大增加，不够灵活。若数据库有K个人，则CNN模型输出softmax层就是K维的。
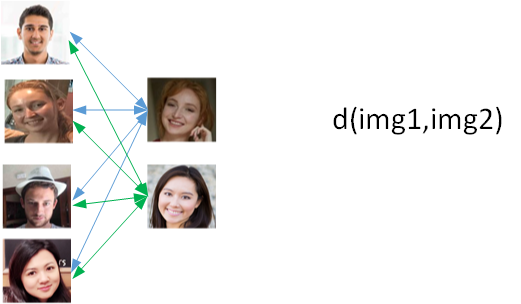
  为了解决One-shot learning的问题，我们先来介绍相似函数（similarity function）。相似函数表示两张图片的相似程度，用d(img1,img2)来表示。若d(img1,img2)较小，则表示两张图片相似；若d(img1,img2)较大，则表示两张图片不是同一个人。相似函数可以在人脸验证中使用：
• \(d(img1,img2)\leq \tau\) : 一样
• \(d(img1,img2)> \tau\) : 不一样
  对于人脸识别问题，则只需计算测试图片与数据库中K个目标的相似函数，取其中d(img1,img2)最小的目标为匹配对象。若所有的d(img1,img2)都很大，则表示数据库没有这个人。
  

Siamese网络

若一张图片经过一般的CNN网络（包括CONV层、POOL层、FC层），最终得到全连接层FC，该FC层可以看成是原始图片的编码encoding，表征了原始图片的关键特征。这个网络结构我们称之为Siamese network。也就是说每张图片经过Siamese network后，由FC层每个神经元来表征。

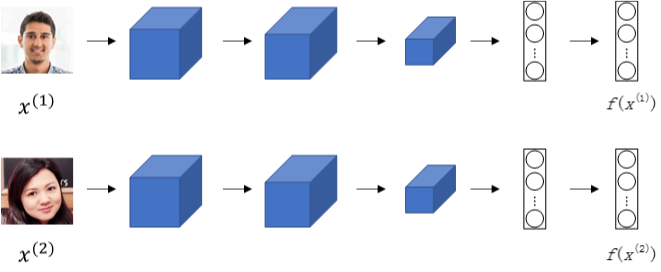
建立Siamese network后，两张图片\(x^{(1)}\)和\(x^{(2)}\)的相似度函数可由各自FC层\(f(x^{(1)})\)与\(f(x^{(2)})\)之差的范数来表示：

\[d(x^{(1)},x^{(2)})=||f(x^{(1)})-f(x^{(2)})||^2 \]

值得一提的是，不同图片的CNN网络所有结构和参数都是一样的。我们的目标就是利用梯度下降算法，不断调整网络参数，使得属于同一人的图片之间\(d(x^{(1)},x^{(2)})\)很小，而不同人的图片之间\(d(x^{(1)},x^{(2)})\)很大。

• 若\(x^{(i)}，x^{(j)}\)是同一个人，则\(||f(x^{(1)})-f(x^{(2)})||^2\)较小
• 若\(x^{(i)}，x^{(j)}\)不是同一个人，则\(||f(x^{(1)})-f(x^{(2)})||^2\)较大

三元组损失

构建人脸识别的CNN模型，需要定义合适的损失函数，这里我们将引入Triplet Loss。

Triplet Loss需要每个样本包含三张图片：靶目标（Anchor）、正例（Positive）、反例（Negative），这就是triplet名称的由来。顾名思义，靶目标和正例是同一人，靶目标和反例不是同一人。Anchor和Positive组成一类样本，Anchor和Negative组成另外一类样本。

我们希望上一小节构建的CNN网络输出编码\(f(A)\)接近\(f(P)\)，即\(||f(A)-f(P)||^2\)尽可能小，而\(||f(A)-f(N)||^2\)尽可能大，数学上满足：

\[||f(A)-f(P)||^2\leq ||f(A)-F(N)||^2 \]

\[||f(A)-f(P)||^2-||f(A)-F(N)||^2\leq 0 \]

根据上面的不等式，如果所有的图片都是零向量，即\(f(A)=0,f(P)=0,f(N)=0\)，那么上述不等式也满足。但是这对我们进行人脸识别没有任何作用，是不希望看到的。我们希望得到\(||f(A)-f(P)||^2\)远小于\(||f(A)-f(N)||^2\)。所以，添加一个超参数\(\alpha\)。且\(\alpha \gt0\)，对上述不等式作出如下修改：

\[||f(A)-f(P)||^2-||f(A)-F(N)||^2\leq -\alpha \]

或者表示成下式：

\[||f(A)-f(P)||^2-||f(A)-F(N)||^2+\alpha \leq 0 \]

\(\alpha\)也被称为间隔（margin）。这个间隔的引入就保证了\(d(A,P)\)和\(d(A,N)\)在识别成功的时候的差值总是较大的。
接下来，我们根据A，P，N三张图片，就可以定义Loss function为：

\[L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-F(N)||^2+\alpha,\ 0) \]

相应地，对于m组训练样本，cost function为：

\[J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)}) \]

关于训练样本，必须保证同一人包含多张照片，否则无法使用这种方法。例如10k张照片包含1k个不同的人脸，则平均一个人包含10张照片。这个训练样本是满足要求的。
然后，就可以使用梯度下降算法，不断训练优化CNN网络参数，让J不断减小接近0。

同一组训练样本，A，P，N的选择尽可能不要使用随机选取方法。因为随机选择的A与P一般比较接近，A与N相差也较大，毕竟是两个不同人脸。这样的话，也许模型不需要经过复杂训练就能实现这种明显识别，但是抓不住关键区别。所以，最好的做法是人为选择A与P相差较大（例如换发型，留胡须等），A与N相差较小（例如发型一致，肤色一致等）。这种人为地增加难度和混淆度会让模型本身去寻找学习不同人脸之间关键的差异，“尽力”让\(d(A,P)\)更小，让\(d(A,N)\)更大，即让模型性能更好。

面部识别与二分类问题的联系

除了构造triplet loss来解决人脸识别问题之外，还可以使用二分类结构。做法是将两个siamese网络组合在一起，将各自的编码层输出经过一个逻辑输出单元，该神经元使用sigmoid函数，输出1则表示识别为同一人，输出0则表示识别为不同人。结构如下：

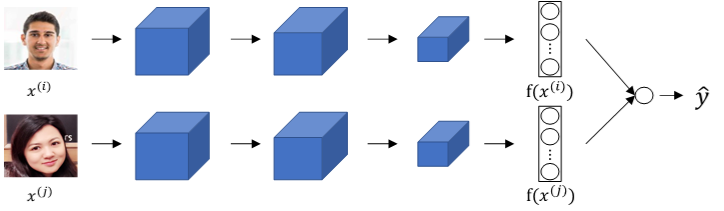
每组训练样本包含两张图片，每个siamese网络结构和参数完全相同。这样就把人脸识别问题转化成了一个二分类问题。引入逻辑输出层参数w和b，输出\(\hat y\)表达式为：

\[\hat y=\sigma(\sum_{k=1}^Kw_k|f(x^{(i)})_k-f(x^{(j)})_k|+b) \]

其中参数\(w_k\)和\(b\)都是通过梯度下降算法迭代训练得到。
\(\hat y\)的另一种表达式为：

\[\hat y=\sigma(\sum_{k=1}^Kw_k\frac{(f(x^{(i)})_k-f(x^{(j)})_k)^2}{f(x^{(i)})_k+f(x^{(j)})_k}+b) \]

上式被称为\(\chi\)方公式，也叫\(\chi\)方相似度。