吴恩达机器学习笔记-14(降维)
降维
降维可以压缩数据,使得数据占用较少的磁盘空间,还可以加速学习算法。
数据压缩
下面看这样一个例子:
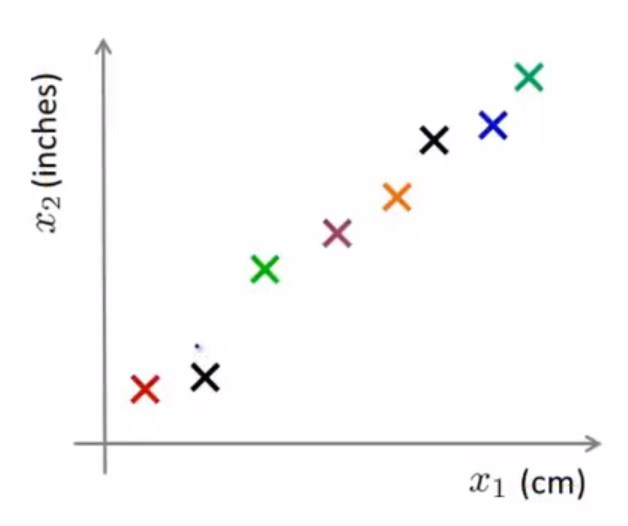
假设这个数据集中的样本有两个特征,两个特征都表示物体的长度,因此是高度冗余的,那么我们会希望将这个2维数据压缩到1维。(因为都是四舍五入之后的数据,所以画出来不会在一条直线上。)
把不同的样本用不同的颜色标注出来
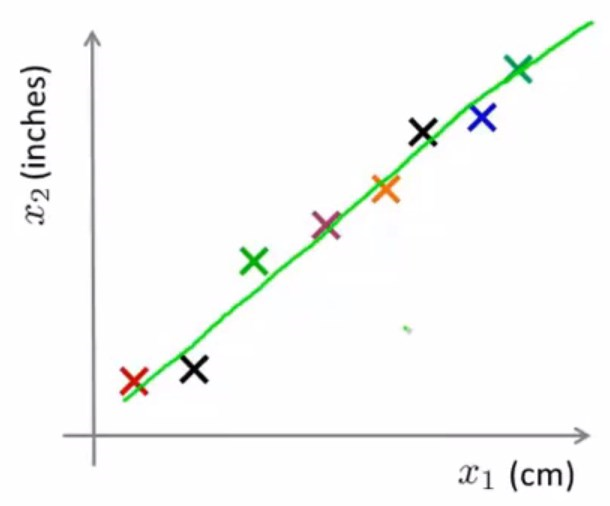
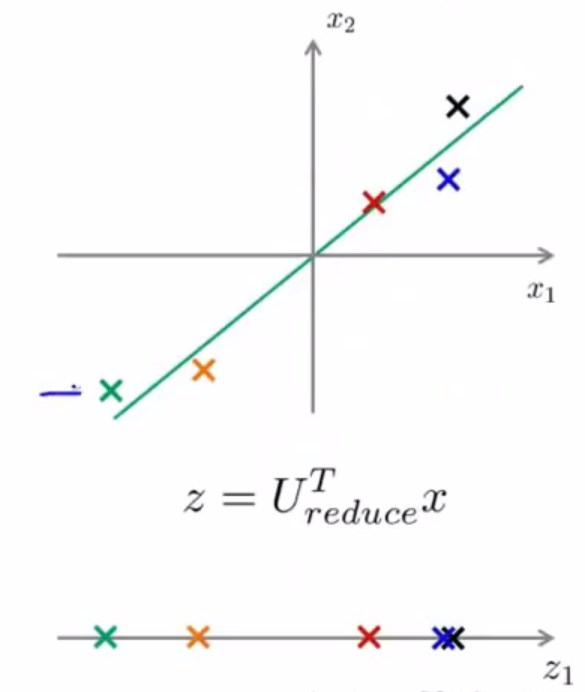
假设有这样一条绿色的线,看起来大多数样本都在的一条线。
我们把所有数据都投影到绿色的线上,那么会得到这样一个结果:

那么就需要新定义一个特征\(z_1\),这个特征可以表示出任意一个样本。
对于原始样本\(x^i\)来说,是2维实数向量。投影过后,或者说降维之后的样本\(z^i\)就应该是1维实数向量。
总而言之就是,如果允许通过投影绿线上所有的原始样本来近似原始的数据集,那么就只需要一个实数,就可以指定任意一个样本在直线上的位置。
这样就可以使数据空间减半,使算法运行更快。
同样可以将3维数据降维到2维数据。在实际工作中,可能会有1000维乃至于10000维的数据,但是这样高维的是无法通过作图观察到的,所以这里举的例子是3维到2维的。
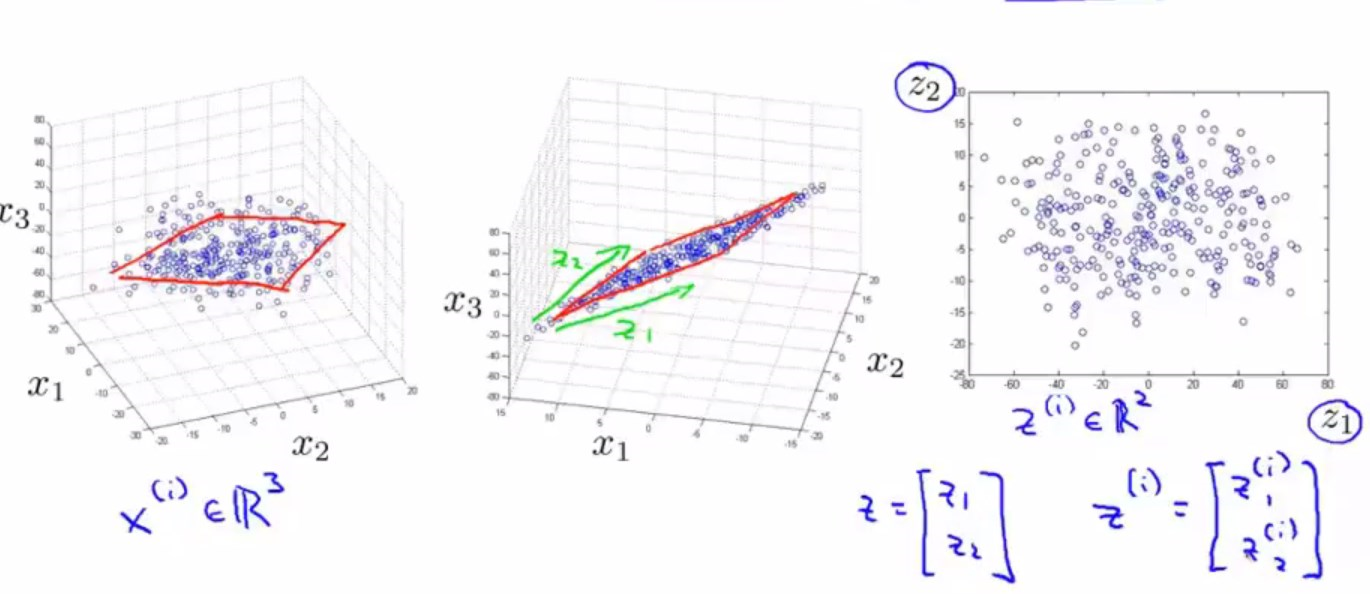
左边是原始的数据集,可能很难看出来,这些数据其实大概都分布在一个平面内,那么我们会想将这些数据投影到同一个平面中,如中间图所示。然后用两个新的特征\(z_1,z_2\)来表示,最后得到右边的平面图。
新数据集的样本显然就应该是2维实数向量,这样就实现了所谓的降维。
数据可视化
降维除了用于压缩数据使得数据占用率变小,算法加快,还可以用于数据可视化。
(2014年数据)
| 国家 | GDP(万亿美元) | 人均GDP(千美元) | 人类发展指数 | 平均寿命 | 贫困指数 | 平均家庭收入 | ...... |
|---|---|---|---|---|---|---|---|
| 加拿大 | 1.577 | 39.17 | 0.908 | 80.7 | 32.6 | 67.293 | ...... |
| 中国 | 5.878 | 7.54 | 0.687 | 73 | 46.9 | 10.22 | ...... |
| 印度 | 1.632 | 3.41 | 0.547 | 64.7 | 36.8 | 0.735 | ...... |
| 俄罗斯 | 1.48 | 19.84 | 0.755 | 65.5 | 39.9 | 0.72 | ...... |
| 新加坡 | 0.223 | 56.69 | 0.866 | 80 | 42.5 | 67.1 | ...... |
| 美国 | 14.527 | 46.86 | 0.91 | 78.3 | 40.8 | 84.3 | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... |
| 假设有50个特征,也就是说\(x^i\)是50维向量,要可视化,就必须要降维,将50维降到3维乃至2维。 |
比起上面这个复杂的表格,将50维向量降到2维:
| 国家 | \(z_1\) | \(z_2\) |
|---|---|---|
| 加拿大 | 1.6 | 1.2 |
| 中国 | 1.7 | 0.3 |
| 印度 | 1.6 | 0.2 |
| 俄罗斯 | 1.4 | 0.5 |
| 新加坡 | 0.5 | 1.7 |
| 美国 | 2 | 1.5 |
| ...... | ...... | ...... |
| 在降维的时候,z通常不会是具有物理意义的特征,也就是说他可能是比较抽象的,但是又能反映各样本不同的一个值。那么在可视化的时候需要做的一件事就是,要弄清楚降维后产生的新的特征,代表什么意思,才能读懂可视化图形所传达的信息。 | ||
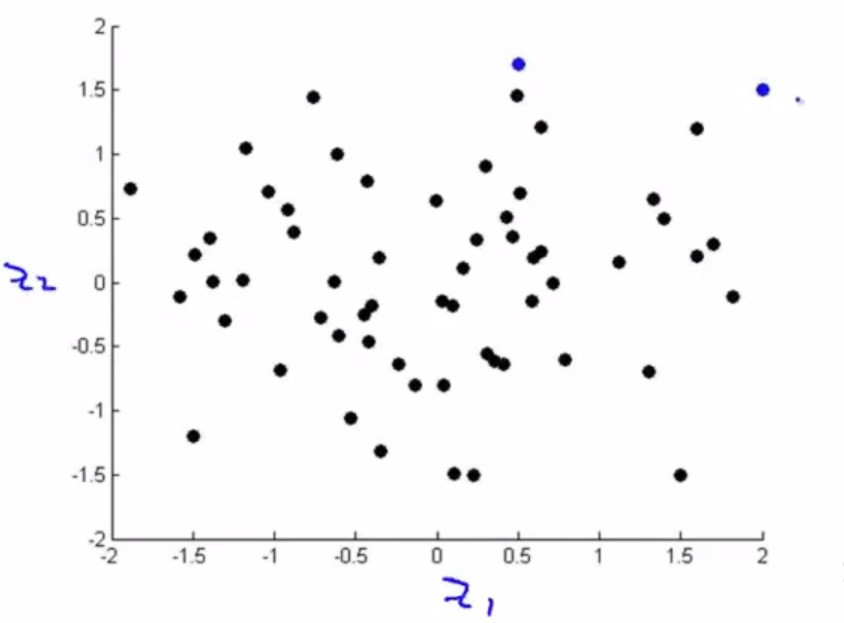
| 把这个新数据集可视化之后可以得到: | ||
 |
||
| 假设\(z_1\)表示国家的经济活跃程度,\(z_2\)表示个人的经济活跃程度或者表示个人幸福程度之类的。 | ||
| 那么靠近右上角的样本,表示这个国家经济体量大,而且人均经济也比较发达或者说人均比较幸福,传统意义上的发达国家。 | ||
| 如果是右方靠下的点,表示这个国家经济体量大,但是人均经济欠发达或者说人均不那么幸福,就比较像现在的中国。 |
这就是如何用降维的方法来进行数据可视化。
主成分分析(PCA,Principal Component Analysis)
对于降维问题,目前最流行最常用的算法是主成分分析法。
假设有这样一个2维数据集,欲降到1维。那么会需要找到一条能将数据投影到上面的直线。
现在需要解决的问题就是,如何去找到这样一条直线,看下面的例子:
若已经找到了一条“好”的直线
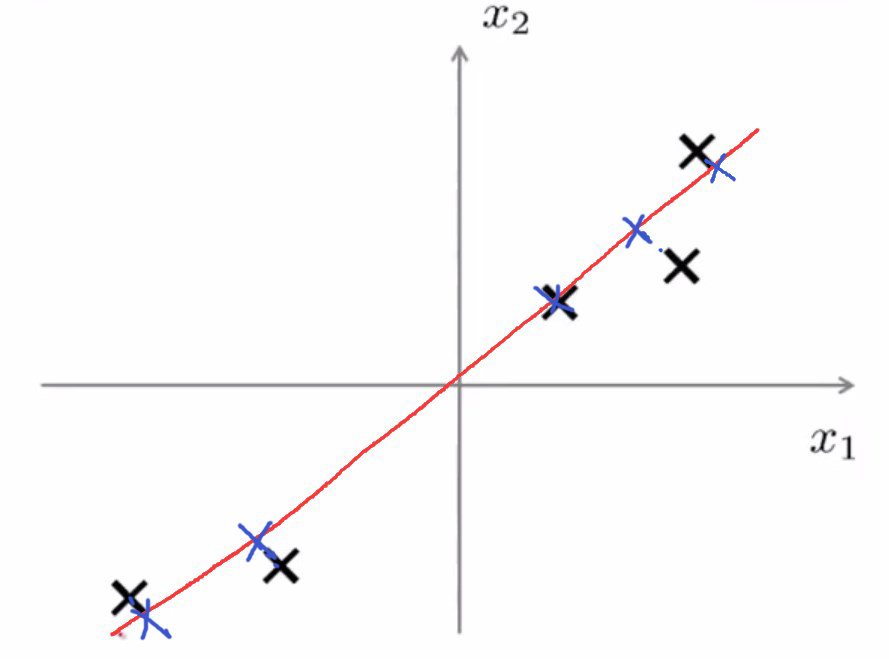
能看出来点到投影点间的垂直距离是比较小的,PCA要做的就是,找到一个低维空间,将数据投影在上面,使得数据与投影点之间的垂直距离(欧氏距离)的平方最小。
这部分欧氏距离有时也称作投影误差,那么根据之前学的内容,容易推断出,就要对这个误差进行最小化。
另外,在运用PCA之前,通常需要进行均值归一化和特征规范化,
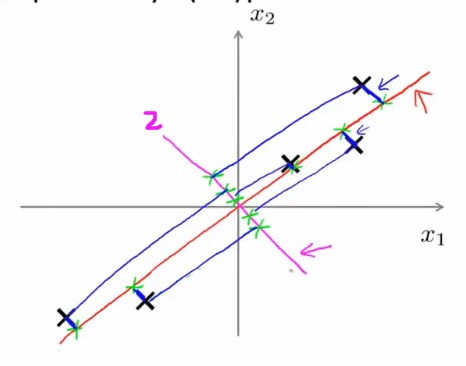
相比之下,投影在2号直线上的点与数据之间的欧氏距离就会非常大,所以PCA不会选择这样一条直线进行降维操作。
更加一般化地说,我们有n维的数据,欲降至k维,不会想上面的直线一样只是找单个向量进行投影,而是找k个方向的向量进行投影,并对投影误差进行最小化处理。
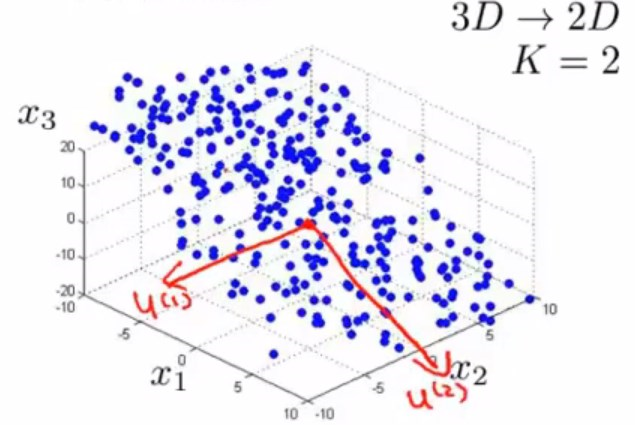
对于3维降2维的例子而言,就是需要找2个方向的向量进行投影,而这2个向量则构成了一个2维平面。
用线性代数化的语言描述就是,需要找k个向量(\(u^1,...,u^k\)),将数据投影到这k个向量展开的线性子空间上面。
算法的使用
首先要对数据预处理,即进行特征缩放或者均值归一化。
计算每个特征的均值\(\mu_j=\frac{1}{m}\sum_{i=1}^m{x_j^i}\),令\(x_j^i=x_j^i-\mu_j\)。如果特征是在不同的数量级上,我们还需要将其除以标准差\(\sigma\)。
抛开数学推导不谈,PCA降n维为k维的过程如下:
- 计算协方差矩阵\(\Sigma=\frac{1}{m}\sum_{i=1}^n{(x^i)}{(x^i)}^T\)
如果训练集数据这样表示\(X=\begin{bmatrix}{x^1}^T\\\\...\\\\{x^m}^T\end{bmatrix}\)
协方差矩阵也可以表示为\(\Sigma=\frac{1}{m}X^T{X}\) - 计算矩阵\(\Sigma\)的特征向量:[U,S,V] = svd(Sigma)(svd指的是奇异值分解法,用eig函数也可以),svd返回三个矩阵U,S,V。我们只需要矩阵U,U是一个n*n的矩阵。经过计算后的U能够看出来是由\(u^1,u^2,...,u^n\)一系列列向量组成的,想降到k维,就取前k个向量。令\(U_{reduce}=[u^1,...,u^k]\)
- k维的新特征\(z^i={U_{reduce}}^T\times{x^i}\),\(x^i\)是nX1的,\(U_reduce\)是nXk的,那么\(z^i\)就是k*1的,即k维向量。这样就得到了新的特征。
至此,我们找到了所谓的新特征来表示旧特征,即用k维特征表示之前的n维特征。
实际上在这个求z的过程中,就已经完成了最小化投影误差的操作。
如何选择主成分的数字k
在PCA算法中我们将n维向量降维到k维向量,这个数字k,是PCA的一个参数,或者说是主成分的数字,或者说是保留下来的主成分的数字k。
首先给出数学表达式:
投影误差:\(\frac{1}{m}\sum_{i=1}^m{||x^i-x^i_{approx}||}^2\)
(这里的\(x^i_{approx}=U_{reduce}\times{z^i}\))
数据的总方差(每个数据与原点距离的平方):\(\frac{1}{m}\sum_{i=1}^m{||x^i||}^2\)
在选择k时,一个常见的经验主导的方法是选择使
的最小的k值。
专业的表达是“99%的方差得到了保留”。从经验上来说99%的保留度是最好的。
在octave\matlab中,使用[U,S,V] = svd(Sigma)这一命令时,其中的矩阵S是一个对角矩阵(除主对角线外的其他元素皆为0)。
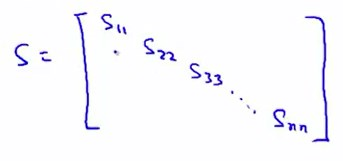
对于给定的k,我们只需要计算是否有:
就可以高效地选择出参数k。
用PCA进行数据重建
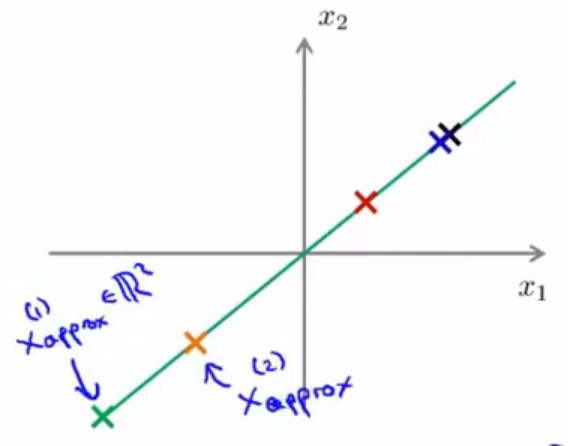
假设有这样一个数据集,已经从2维降到了1维,要将1维数据还原到2维的,考虑到新特征z是k1的向量,原始特征x是n1向量,\(U_{reduce}\)是n*k阶矩阵。
那么容易得到\(x_{approx}^i=U_{reduce}\times{z^i}\),如果投影误差不太大,那么就可以将\(x_{approx}\)近似为原始的特征\(x\)
使用PCA时的注意事项
考虑这样一个监督学习的例子:
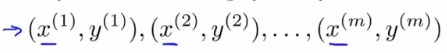
有m个样本,每个样本又10000个特征(即\(x^i\)是一个10000维向量)
只对数据集中的特征\(x^1,...,x^m\)使用PCA,得到映射出的新特征\(z^1,...z^m\)(假设\(z^i\)是1000维向量),这样就通过降维节省了空间,提高了算法运行速率。
此时就有了一个新的训练集
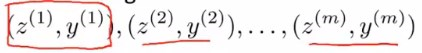
假如用在LR中,函数模型就应该变为对z的函数模型:\(h_\theta(z)=\frac{1}{1+e^{-{\theta^{T}}z}}\)
PCA做的事是用x映射出z,这个映射只能通过在训练集上运行PCA来定义。
经验上来说,在设计学习算法的时候,首先用原始数据来进行学习比一来就用PCA映射出新数据再进行学习更好。只有当使用原始数据不能实现,或者需要的空间太大的时候,再考虑用PCA处理数据之后进行学习。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号