吴恩达机器学习笔记-6(Octave)
Octave
Octave能够更好地实现并快速地掌握机器学习算法。之后再用Java、C++或Python之类的语言去重新实现,会节约很多时间。Octave和MATLAB几乎完全相同,因为Octave开源且免费,安装使用起来比MATLAB更方便,所以我在这里选择使用Octave作为我机器学习入门的语言。
基本操作
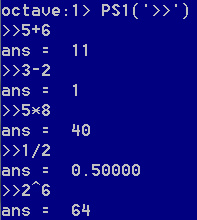
四则运算是基本功能,也可以进行高次运算。最上面一行是一个有趣的命令PS1('>>')这个命令可以更改等待命令的样式,使界面看起来更简洁。
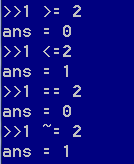
逻辑运算在此处会如其他编程语言一样,返回一个布尔值,1表示True,0表示False,要注意的是,octave里的不等于,应该写成~=,而不是其他编程语言中的!=。

异或运算

Octave中用%来进行注释,%后面的代码不会执行。
变量
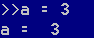
可以使用 a = 3 给变量 a 赋值 3 ,该句命令会一并打印结果
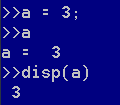
如果在a = 3后面加上一个分号,则不会打印结果,但是仍然会将3赋值给变量a
在 Octave 中 " ; " 不会将语句的执行结果输出。
如果想打印变量 a 的值,只需输入变量名,或者使用命令disp(a)。
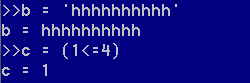
除了可以将数值赋值给变量,也可以将字符串或者布尔值赋值给变量
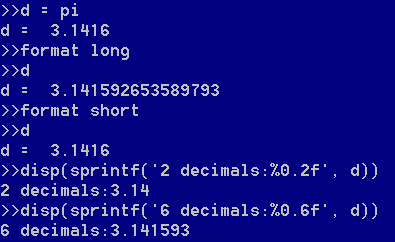
format long 命令输出字符串默认的位数。
format short 命令输出少量小数点后位数。
也可以使用类似C语言风格的格式化字符串来控制打印结果, "%0.2f" 表示 代替d放在这里 并显示d值的小数点后两位数字 。(注: pi 为圆周率 π 。)
向量和矩阵
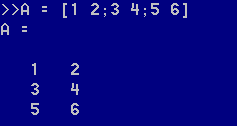
分号表示在矩阵内换到下一行。
空格分隔同一行不同列的元素。
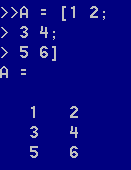
运用前面讲过的分号的特性来建立矩阵也是可行的。

那么容易知道建立向量的方法

V=1:0.1:2表示从1开始以0.1为步长递增到2,建立一个向量,容易想到,这是一个11列的行向量。默认以1为步长。
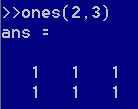
ones(2,3)表示生成一个元素全为1的2*3的矩阵。
zeros则表示生成元素全为0的矩阵
rand表示生成元素全为随机值的矩阵
randn表示生成的元素符合高斯分布的矩阵
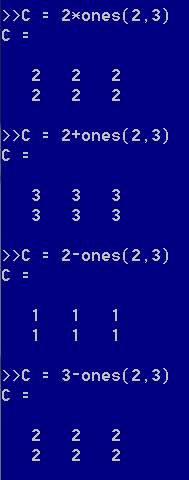
容易想到,可以运用矩阵的运算来生成不同的矩阵
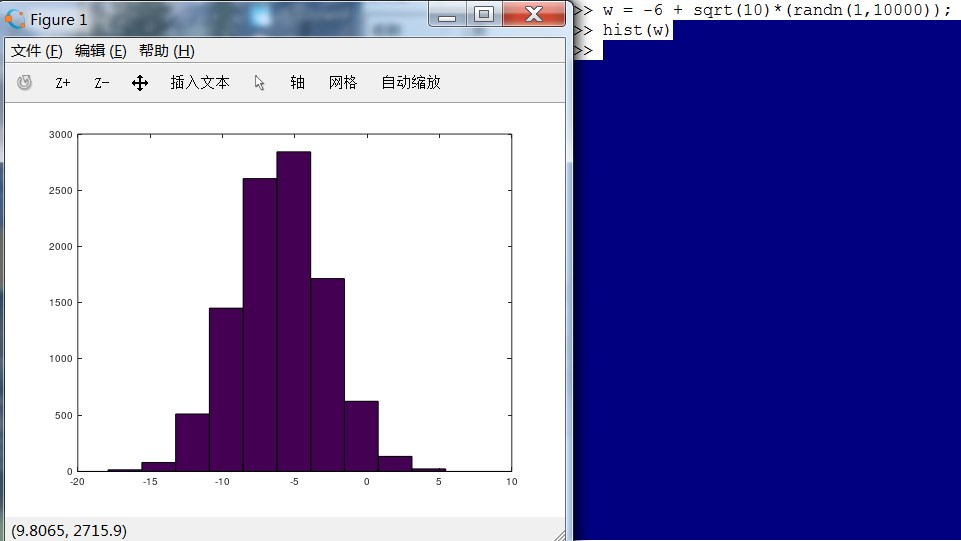
hist命令用于打印直方图
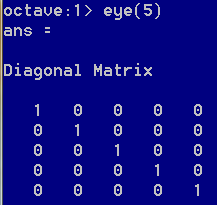
eye命令用于生成单位阵
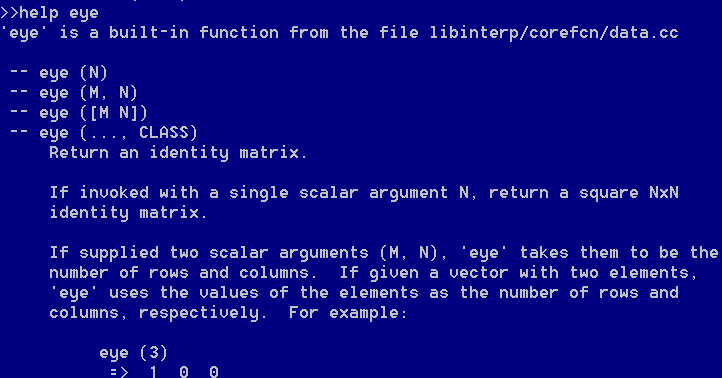
类似python,help命令可以查询内置函数的作用。
quit或者exit可以退出octave。
移动矩阵中的数据
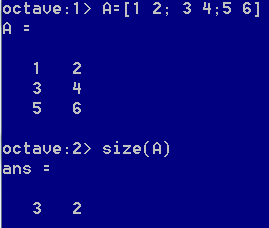
size可以读取矩阵的尺寸,该方法返回的也是一个矩阵。
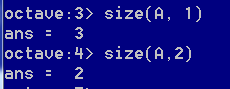
可以分别返回矩阵A的行数和列数

length会返回矩阵最大的维度

pwd命令会显示octave当前所处的路径
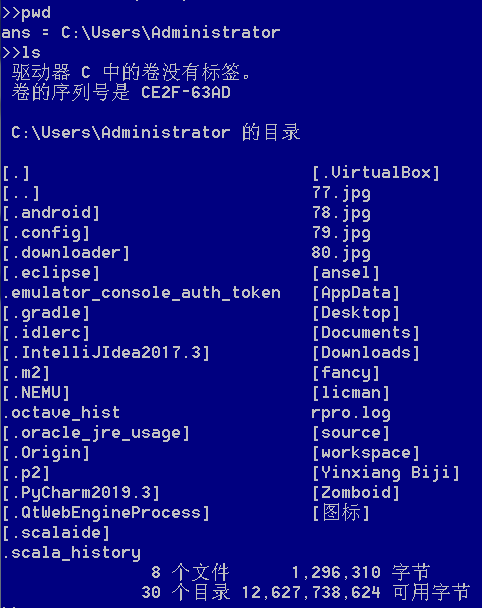
ls命令会列出当前所处目录下的所有文件,类似于unix/linux系统命令
who命令可以显示出当前工作空间中存在的变量
load xxxx.dat命令可以将外部数据导入到工作空间中
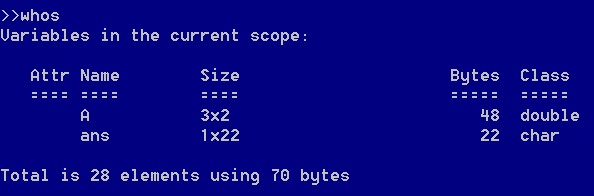
whos命令可以更详细地显示出变量的信息
将priceY的前10个元素赋给变量v
save命令会将变量v以二进制的形式存储到当前工作空间(即前面pwd命令显示的那个地址)中的指定文件里

clear命令会清除掉当前工作空间的所有变量
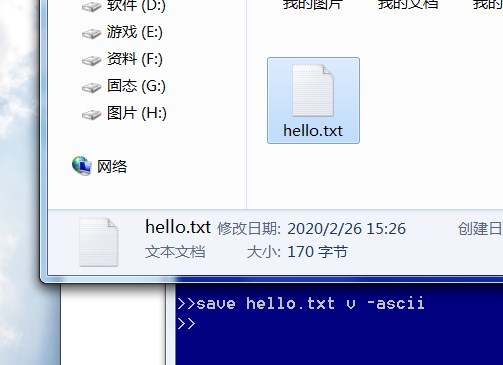
这个命令会将变量v,或者说将变量v的ASCII值存为文本文档
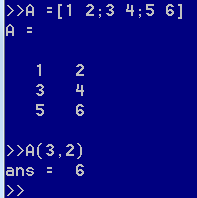
Ocatve中同样可以通过索引来读取单个元素的值
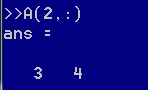
“:”表示某行/列的每一个元素
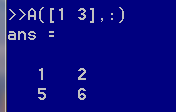
表示第1行和第3行的每一个元素

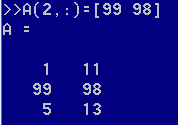
也可以通过索引来更新
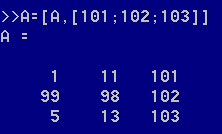
这样可以在原矩阵右边连接一个新矩阵,左边同理。(逗号可加可不加)

这样可以将A中所有元素放进一个向量中
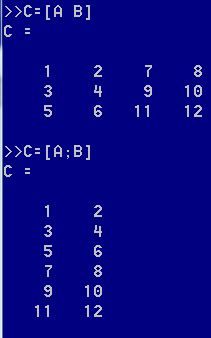
分号表示添加在下面,因为分号的含义是下一行,所以会换行连接矩阵
矩阵运算
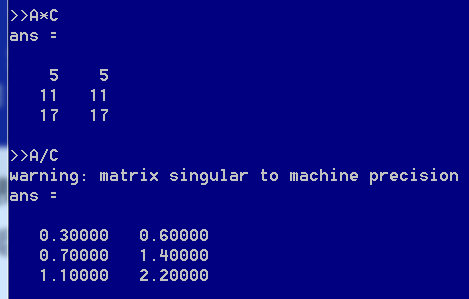
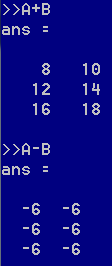
四则运算是可行的。


在octave中,“.”表示对元素位进行运算,这行代码表示将A中每个元素与B中每个元素相乘

单引号表示转置
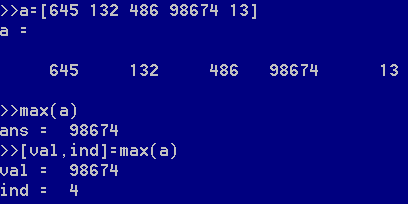
max函数会返回最大值和最大值所在的索引
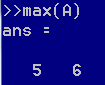
如果对象是一个矩阵,则会查找每列的最大值

每个元素返回一个布尔值

返回结果为真的索引
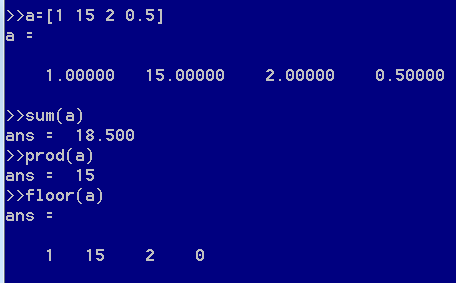

sum函数返回所有元素之和
prod函数返回所有元素之积
floor函数对所有元素进行向下四舍五入
ceil函数对所有元素进行向上四舍五入
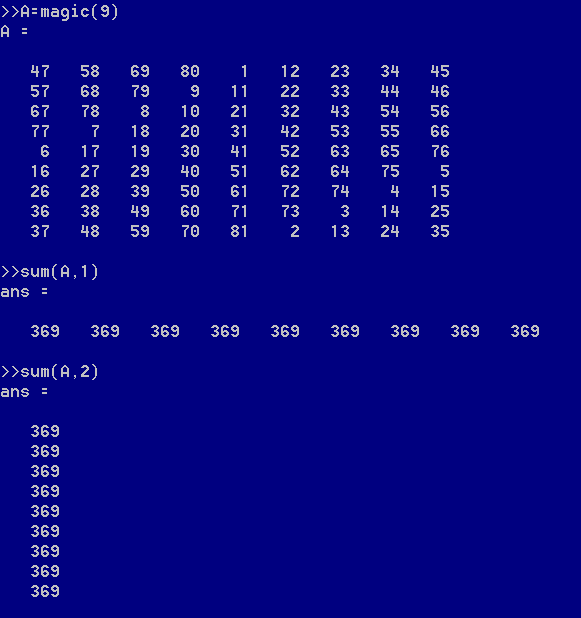
magic函数可以生成一个指定阶数的幻方
此处的sum函数中,1和2分别表示矩阵A的第1个维度和第2个维度
数据可视化
octave可以方便地对数据进行可视化操作
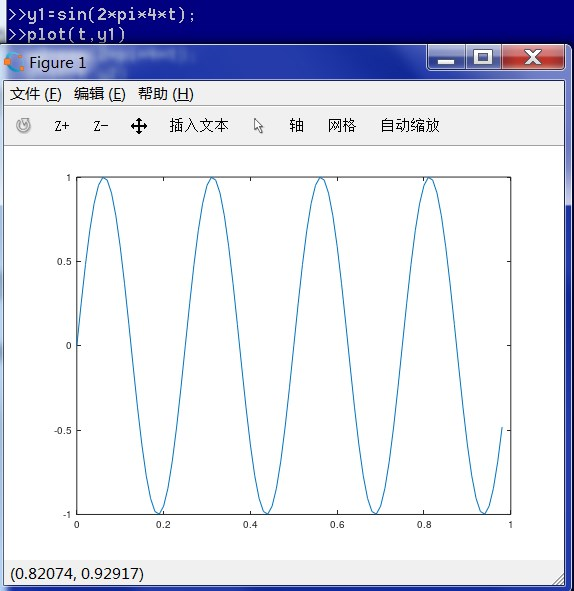
其中t=[0:0.01:0.98]
plot函数可以返回一个二维函数图像
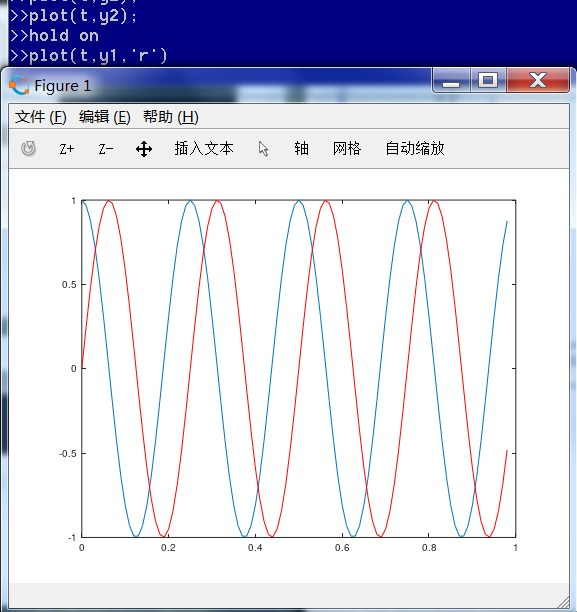
hold on命令可以将另一个函数图像与之前的置于统一坐标系中
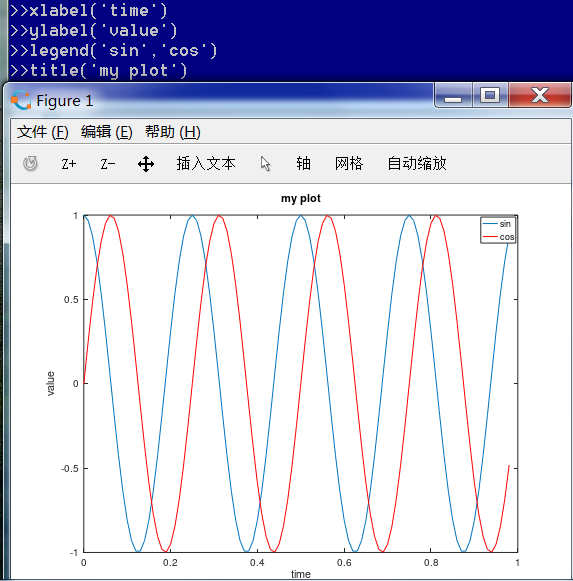
xlabel、ylabel、legend、title命令分别可以对函数图像的信息进行编辑
print -dpng 'myplot.png'命令可以将图像保存到当前工作空间
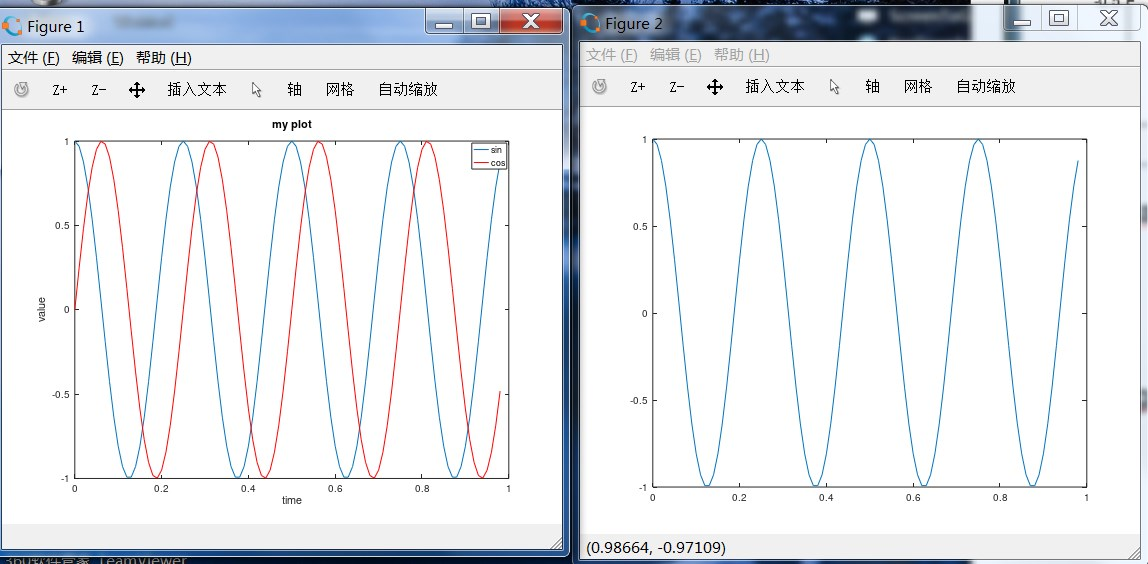
figure(2):plot(t,y2)命令可以打开新窗口并绘制函数图像
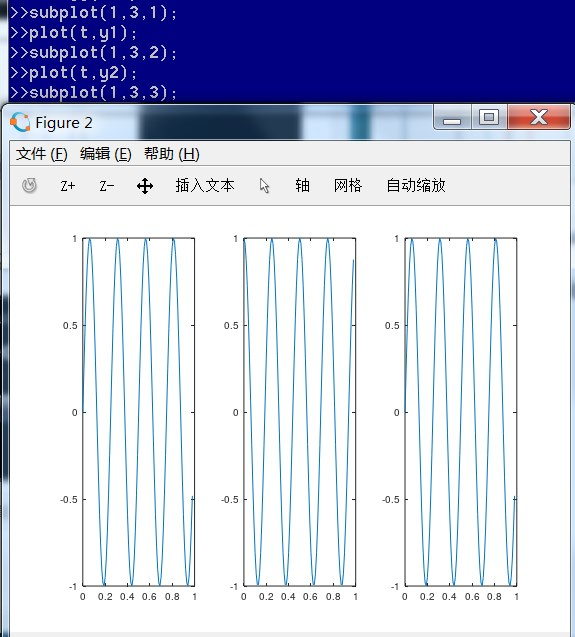
subplot命令可以将一个图像窗口分隔为多块显示,如图中的subplot(1,3,1)命令,指的是将窗口分隔为1*3的格子来分别绘制不同的函数图像,最后一个1指的是第1个格子
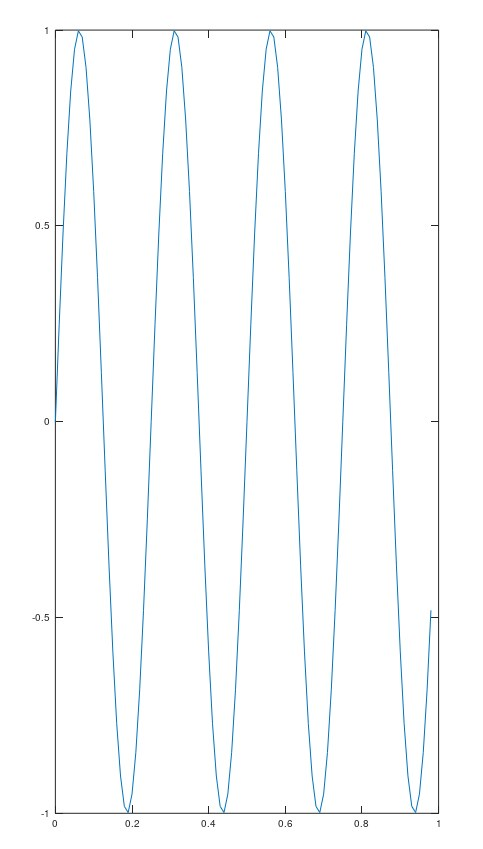
axis命令可以更改坐标轴的显示范围,如axis([0.5 1 -1 1])中,前两个数字表示X轴,后两个数字表示Y轴,Octave会自动地将坐标轴调整为相同的比例
clf可以清空一个图像窗口
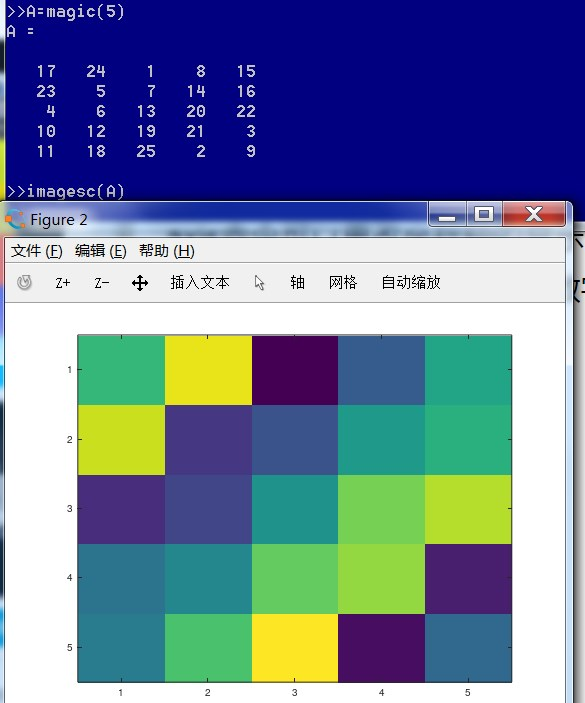
imagesc函数可以返回一个彩色格子图,不同颜色对应于矩阵A中不同的值

imagesc(A),colorbar,colormap gray可以生成一个灰度分布图colorbar可以生成一个色度条表示不同颜色对应的不同值
控制语句
for循环

也可以构建一个索引,将索引的值赋给i,达到指定循环条件的效果
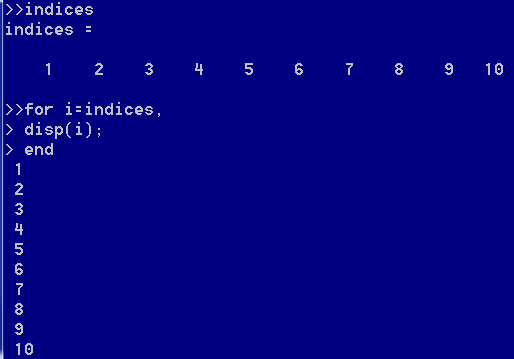
while循环

if-elseif选择
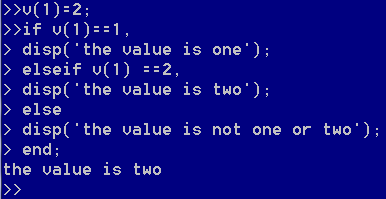
嵌套
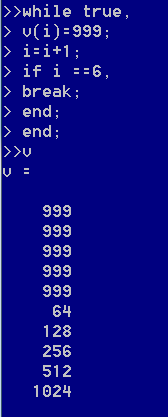
控制语句嵌套,注意end;作为哪个控制体的结尾
函数定义与使用
Octave中,想要使用自定义的函数,首先需要创建一个以.m为后缀的文件


该函数只有两行代码。
第一行告诉Octave我需要squareThisNumber函数返回一个值,并将这个值赋给变量y,同时squareThisNumber函数有一个形参x。
第二行代码是函数体,里面是该函数具体的执行方法。

调用函数要保证,定义的函数文件与当前Octave所处工作空间在同一路径下,使用pwd命令来确定当前工作空间,或者用cd命令来改变当前工作空间。

要注意Octave是通过文件名来调用函数的,我在此处犯了一个错误,我误将函数名写成了小写,而文件名是大写,但是编译同样通过,甚至输出了正确的答案,因此在以后的编程中,应当注意,保证文件名与函数名匹配。
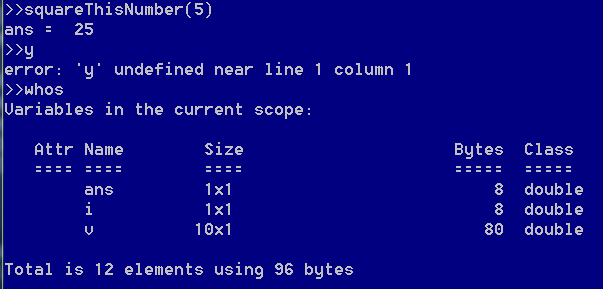
此处还有一个地方需要注意,函数中定义了将值赋给变量y,但是实际上工作空间中是不存在变量y的。和其他语言也是类似的,函数中的局部变量只在函数中起作用。因此应当注意区别变量名,避免混淆。
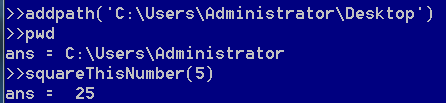
Octave提供了添加搜索路径的功能,可以添加欲搜索的路径,这样即使函数文件不在当前工作空间中,编译器也知道去哪里搜索这个函数。
多返回值函数

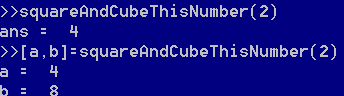
因为返回的多个值,是以列表的形式存储的,所以必须要在控制台以列表的形式接收,才能全部打印出来,否则
代价函数实践
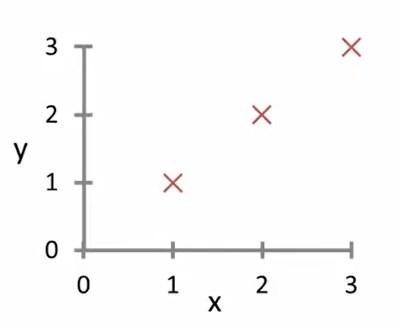
有这样一个数据集\([x,y]=[1,1;2,2;3,3]\)
|---|---|---|
|\(x^0\)|\(x^1\)|\(y\)|
|1|1|1|
|1|2|2|
|1|3|3|
容易得到假设函数\(h(x)=\theta_0+\theta_1{\times}x\)我们需要利用octave来计算代价函数,求出一个\(\theta\)值使得代价函数值最小
首先构建一个设计矩阵(design matrix)
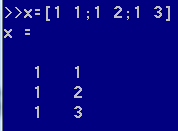
第一列是为了便于计算约定的\(x^{(0)}=1\),第二列即是三个样本各自的特征值。
然后构建一个结果y的矩阵
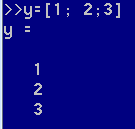
因为只有一个特征值,所以容易得到假设函数\(h_{\theta}(x)=\theta_0+\theta_1{\times}x\)
回顾之前所学,容易得到代价函数\(J(θ_0,θ_1)=\frac{1}{2m} \sum^{m}_{i=1}{(h_θ(x_i)-y_i)^2}\)
根据算法要求编写自定义的函数costFunctionJ
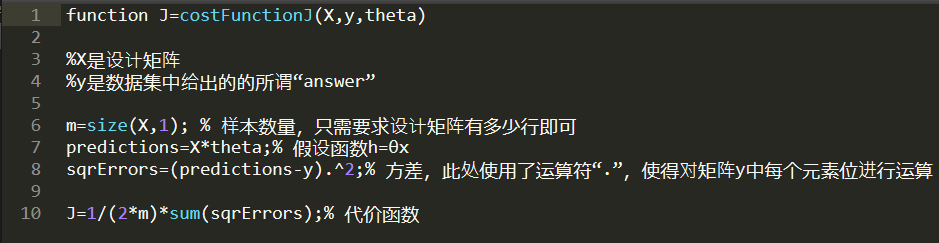
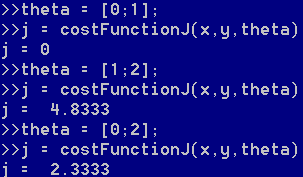
此处定义的变量theta表示假设函数中的\(\theta_0,\theta_1\)的值。
那么经过计算,容易得出当\(\theta_0=0,\theta_1=1\)时,代价函数的值最小。
octave\matlab的优势在于有许多内置的数学相关的库,进行数学运算时会比其他语言快得多得多。
向量化
很多时候我们可以将复杂的方程或者函数表示为向量或者矩阵运算的结果。
前面的多元线性回归章节中有提到过关于假设函数\(h_θ(x)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_4+……+θ_nx_n\)的向量化例子
\(x=\begin{bmatrix} x_0\\\\ x_1\\\\ x_2\\\\…\\\\x_n \end{bmatrix}\) \(θ=\begin{bmatrix} θ_0\\\\ θ_1\\\\ θ_2\\\\…\\\\θ_n \end{bmatrix}\)
对于这个假设函数,如果要用普通的for循环来实现的话,应该如下
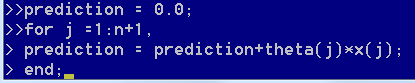
这里需要注意的是,数学上\(\theta\)的下标是从0开始的,但是在octave\matlab中,下标是从1开始的,所以需要建立从1到n+1的索引才能正确对应
如果使用向量化呢?

一行代码即可,所利用的就是matlab\octave高度优化的数值线性代数(数值线性代数:研究在计算机上进行线性代数计算的学科)算法来计算,不仅实现起来简单,运行起来也更加高效。
梯度下降实例
在多元线性回归模型中,梯度下降法中对参数\(\theta\)进行每次迭代时,式子如下:
\(θ_0:=θ_0- α\frac{1}{m} \sum^{m}_{i=1}{(h_θ(x^i)-y^i)x_0^i}\)
\(θ_1:=θ_1- α\frac{1}{m} \sum^{m}_{i=1}{(h_θ(x^i)-y^i)x_1^i}\)
\(θ_2:=θ_2- α\frac{1}{m} \sum^{m}_{i=1}{(h_θ(x^i)-y^i)x_2^i}\)
\((n=2)\)
我们将其向量化为:
\(\theta:=\theta-\alpha\delta\),其中\(\theta\alpha\delta都是n+1维向量\)
下面详细分析一下为何\(\delta\)是一个n+1维的向量
且其中\(\delta=α\frac{1}{m} \sum^{m}_{i=1}{(h_θ(x^i)-y^i)x^i}\)
那么有\(\delta_0=α\frac{1}{m} \sum^{m}_{i=1}{(h_θ(x^i)-y^i)x_0^i}\)
根据假设函数的定义,以及y的定义,我们容易知道\(h_θ(x^i)-y^i\)
是一个实数,而\(x^i\)是一个向量
\(x^i=\begin{bmatrix} x_0^i\\\\ x_1^i\\\\ x_2^i \end{bmatrix}\)
再看下面这个式子
在\(n=2\)的情况下,\(\sum^m_{i=1}(h_θ(x^i)-y^i)\times{x^i}=(h_θ(x^0)-y^0)\times{x^0}+(h_θ(x^1)-y^1)\times{x^1}+(h_θ(x^2)-y^2)\times{x^2}\)
前面提到过\((h_θ(x^i)-y^i)\)是一个实数,而\(x^i\)是一个向量,根据矩阵\向量运算法则,实数乘一个矩阵\向量其结果仍然是一个矩阵\向量,而多个矩阵\向量相加,其结果依然为矩阵\向量,故而\(\delta\)是一个n+1维的向量
comment:可以表示为:
comment:\(\sum={\begin{bmatrix} (h_θ(x^0)-y^0)&(h_θ(x^1)-y^1)&(h_θ(x^2)-y^2) \end{bmatrix}}\times{\begin{bmatrix} x_0^i\\\\ x_1^i\\\\ x_2^i \end{bmatrix}}\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号