10.4总结（未完成）

T1

期盼：100 实际：100

以前做过的一道题，因为k=|i-j|，而|i-j|的最小值即为gcd(a,b)，所以求gcd，然后用n去除再判断一下奇偶性就好了。

T2

期盼：100 实际：60

错误原因：方法错误，未想到正解

方法：线段树二分

考场上完全没有想到这道题的正解是线段树，用multiset加上优化写的暴力程序。对于这道题，我的思路从一开始就是错误的，因为题目中min富人一定大于等于max穷人，所以具有单调性，是可以用线段树二分来解决的，通过二分查找来删除统计富人个数，而且二分+单点修改stl表是不支持的。

大概就是1. 先把线段树离散化，把权值按大小来排序2. 然后根据权值来建树，我是单点修改，动态加点3. 对于权值小于0的，再写一个操作用来删除点，因为是单点修改，所以不用写pushdown，注意没有查找到就不修改4. 最后写一个操作用来统计答案，我是直接统计富人的个数。从最大（右边）开始加入，直到再加一个会大于sum/2。如果加到了单点，则判断加入后是否更优，更优才加入。

正解时间复杂度为：\(O(nlogn)\)

T3

期盼：40 实际：40

在这里特别感谢@M_sea 大佬

谢邀，在考场上就只会打暴力程序了，谁能在考场上直接推出公式啊！！

通过视频/大佬的题解，我们可以把这道题分成三个部分。

1. 以\(a_i\)为边权，求出最短路。记录点A为\(a_x=\sum{a_i},a_y=\sum{b_i}\)
2. 以\(b_i\)为边权，求出最短路。记录点B为\(b_x=\sum{a_i},b_y=\sum{b_i}\)
3. 求点C，直到点C不在点线段AB的左下方，每次求最短路都记录答案，输出最小值（包括前面两次）。

因为最短路的求法有：

1. 朴素Dijkstra,\(O(n^2)\)
2. 堆优化Dijkstra,\(O(nlogm)\)
3. Bellmax_ford,\(O(nm)\)
4. Spfa,\(O(n)~O(nm)\)
5. Floyd,\(O(n^3)\)

所以在上述三个阶段中的求最短路我们使用堆优化的Dijkstra

补充（关于为什么到C不在线段AB左下方才停止）：

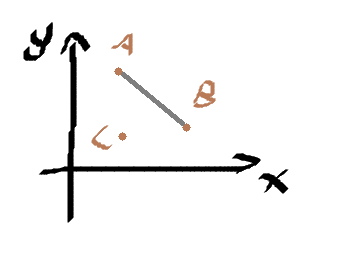
上图是A，B，C三点投影到二维平面的位置，而我们求的是\(x*y\)最小的点，而C的值明显小于A，B点的值。

显然当一个点在AB的左下方时，这个点一定比AB更优。所以我们要使C离AB最远，即\(S _△ABC\)最大，而\(S_△ABC=-\overrightarrow{AB}×\overrightarrow{AC}/2\),所以我们实际上只要让\(\overrightarrow{AB}×\overrightarrow{AC}\)最小就行了。

而由大佬的推导可得：\(\overrightarrow{AB}×\overrightarrow{AC}=(b_x-a_x)c_y+(a_y-b_y)c_x+一个常数\)
所以只要使\((b_x-a_x)c_y+(a_y-b_y)c_x\)最小就好了。
把边权变为\((b_x-a_x)b_i+(a_y-b_y)a_i\)再来算一遍最短路，记录\(\sum{a_i}*\sum{b_i}\)就好了。

T4

期盼：20 实际：0