10.3总结（未完成）

T1

期盼：100 实际：66

错误原因：当\(a_i<0\)时，没有抵消

它的正解方法十分迷惑，我到现在也没有搞懂为什么当\(a_i<0\)时要抵消

先写方法，原理等我搞懂后写。

对于S，当S大于0时：1. 当\(v_i\)大于0时直接加入 2. 当\(v_i\)小于0时用最小抵消后加入 3. 加入后小于0，清除所有 4. 加入后大于S，减最大，直到小于S

当S小于0时：直接记录有多少个\(a_i \geq S\)即可。

T2

期盼：50 实际：88

错误原因：没写倍增，tle

反思：打暴力程序的时候，先判断它的复杂度是否可以通过，在考场上不要打复杂度要爆的暴力（不同数据点可以分开打），打完暴力后尽量去优化，可能万一就过了。这次考试就因为没有用倍增来优化才挂掉。

方法：\(f_{i,j}\)倍增求点i的祖先中第\(2^{j}\)个大于\(a_i\)的点。再倍增判断方案的首尾，维护差值。

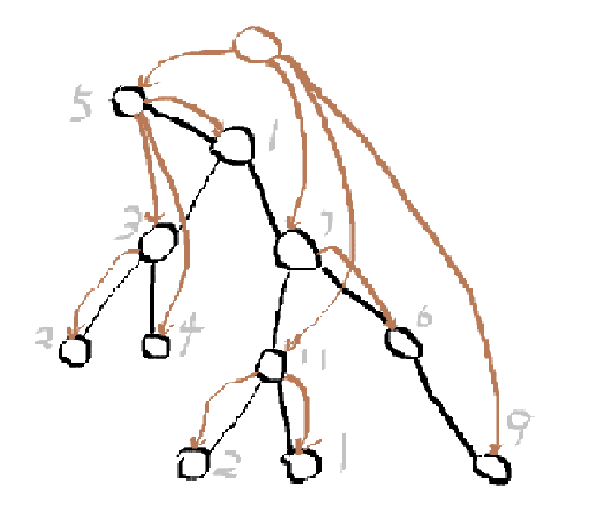
棕色的边为有效边，倍增求点在棕色的树上祖先。

对于每一个任务，找到从u点出发（包括u点）第一个大于c的祖先和深度不超过v的最后一个祖先，求差值，如果差值小于0则没有输出0。

T3

期盼：10 实际：10

没有完全搞懂，搞懂后再添
主要方法：二分枚举mid。对于树上的节点x，记录其到以x为根的子树左边第一个叶子节点的距离和右边第一个叶子节点的距离，且其中间叶子节点两两距离不超过mid，到两边的距离不超过mid。所以对于节点x，用集合记录距离的二元组。找到最小的mid即为答案。

T4

期盼：20 实际：20

考场上，只打出了暴力程序。（对于每次询问，枚举求[l,r]中不同数的出现次数，再单调队列求解，时间复杂度\(O(n^2)\)）

下次遇见此类题，看是否可以用莫队/分块，来优化多次询问的区间查找。

莫队/分块预处理出现次数，因为对于[l,r]这个区间，产生贡献的只有出现次数。考虑根号分治，对于出现次数小于T的，枚举；大于T的，单调队列，时间复杂度为\(O(n\sqrt{n})\)。没有改完，只是理解了思路，具体实现上还是有问题。