KMP算法

字符串匹配：我们经常需要从一个主串（abcabdabcabej）中查找是否包含另一个匹配串 (abcabe)。

Knuth-Morris-Pratt算法（简称KMP）是最常用的匹配算法之一，能帮我们快速进行字符串匹配。

1. 核心思想

1.1 传统匹配思想

1. 第一次匹配

比较标红的 a, 发现主串和匹配串一致，此时比较下一位

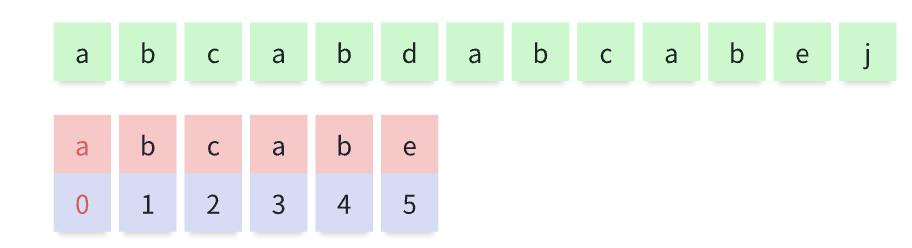
2. 第二次匹配

比较标红的 b，仍然一致，继续向后比较，以此类推

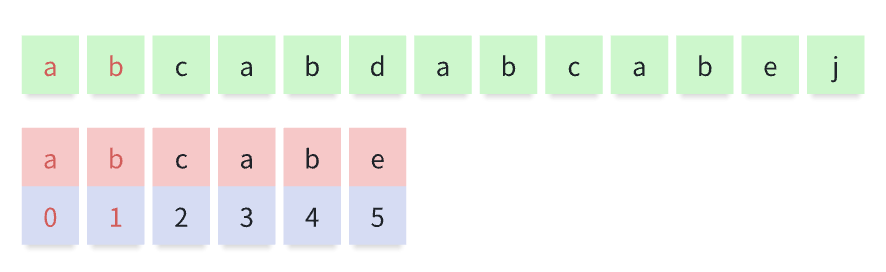
3. 匹配到不一致数值

只要发现紫色位置 ，主串的 d 和匹配串的 e 不一样

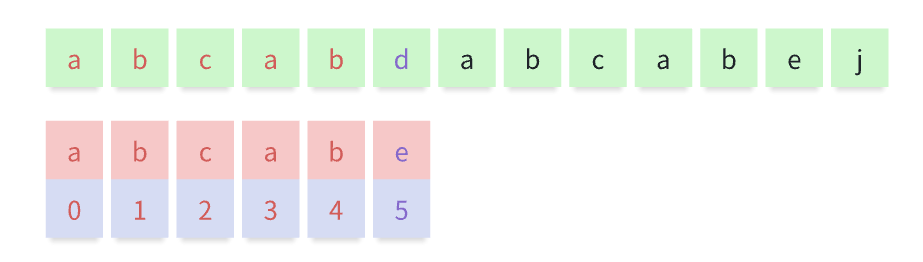
此时传统的暴力方法是从匹配串的 0 下标 a ，从主串的第二位 b 重新开始匹配

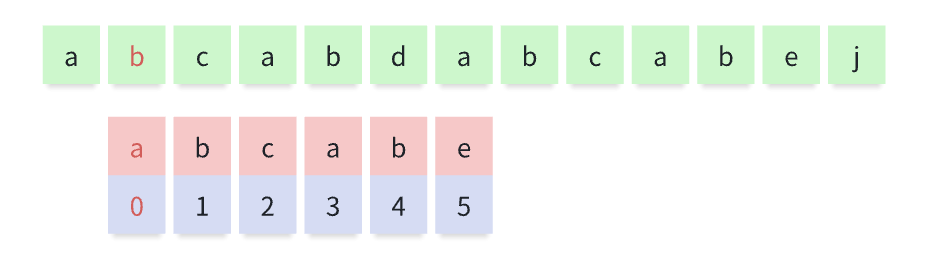
发现不一致时继续后移，以此逻辑循环下去

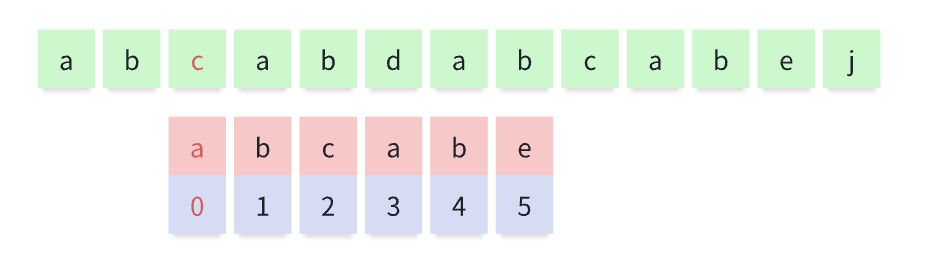
直到完全匹配，明显循环多次，很慢

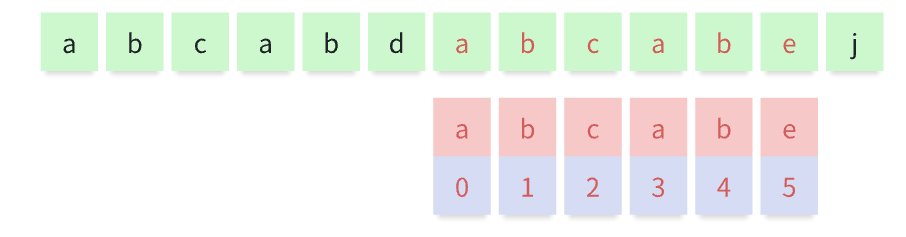
1.2 KMP思想

回到传统的第3步，匹配不一致的情况

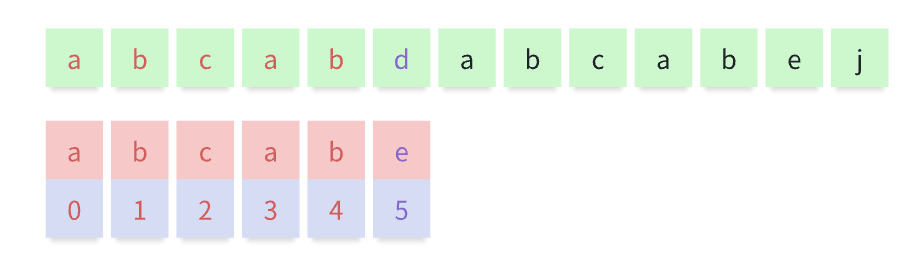
可以观察到主串的bc位置根本不需要比较匹配串，不可能匹配上

主串标红的ab位置虽然需要比较匹配串，但是匹配串的最后两位刚好是ab

所以完全可以从匹配串的下标2位置开始比较下一位

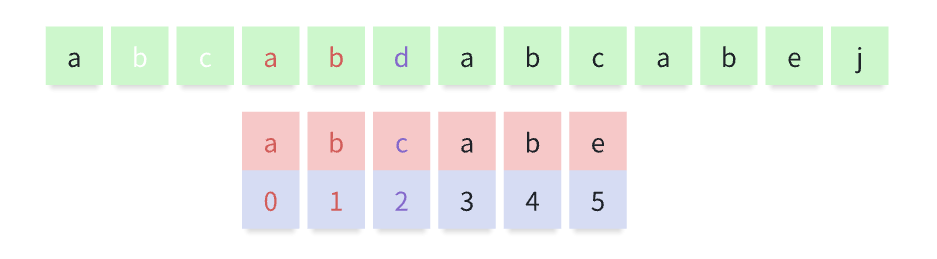
上面这步就是KMP的核心，利用上面的规则记录下每次不匹配时可以直接回退的位置，避免不必要的匹配，从而提高查找效率

2. KMP实现

KMP想实现上述的能力，需要借助前缀后缀表和next数组

2.1 前缀后缀表

所有子串

针对模式串 abcabe 而言，找到它所有子串，再针对每个子串列出前后缀

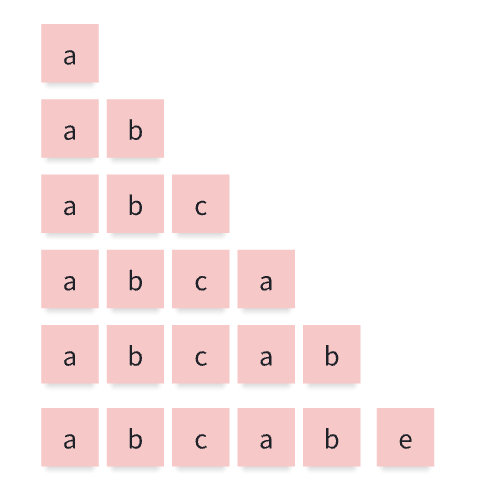
前后缀表

我们针对其中一个子串 abcab 为例 ，求该子串的前后缀列表

前缀 指除了最后一个字符以外，一个字符串的全部头部组合

后缀 指除了第一个字符以外，一个字符串的全部尾部组合

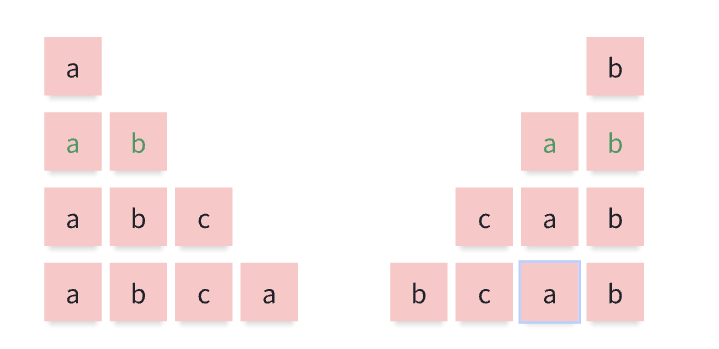
再针对子串 abc 举例

2.2 next数组

公共元素最大长度

观察前后缀表，找出左右一致的，如子串 abcab 存在 ab 既是前缀又是后缀

此时 ab 就是公共元素，如果有多个满足的上述条件的，取最长的作为公共元素最大长度

这里子串 abcab 的公共元素最大长度为 2 ，子串 abc 的公共元素最大长度为 0

其他子串的公共元素最大长度，同理计算如下图

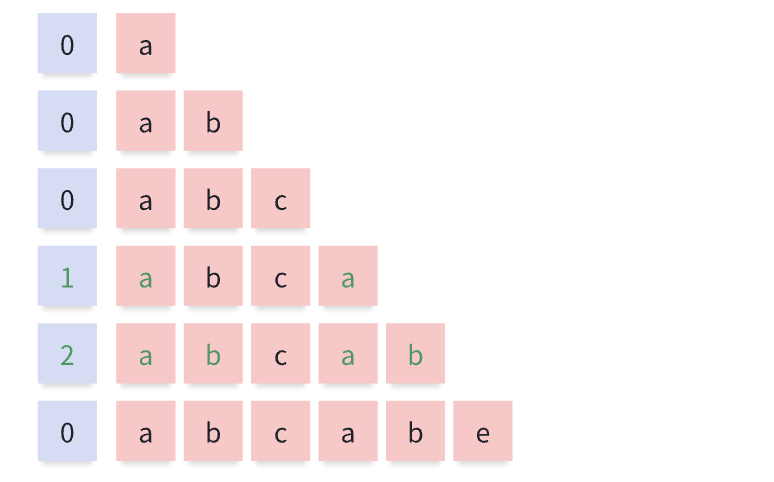
next数组

可以发现，满足公共元素的就可以在匹配异常时跳跃匹配，因为前后缀完全一致

而该跳到哪个位置是根据公共元素最大长度决定，记录下了next数组

next数组其实就是对匹配串每个子串可以回滚的最大位置的下标记录

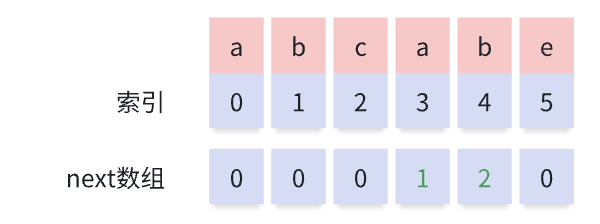
2.3 流程

回到 1.2 KMP思想的图图，当发现下标5的位置不一致时，向前找一位next数组，对应2

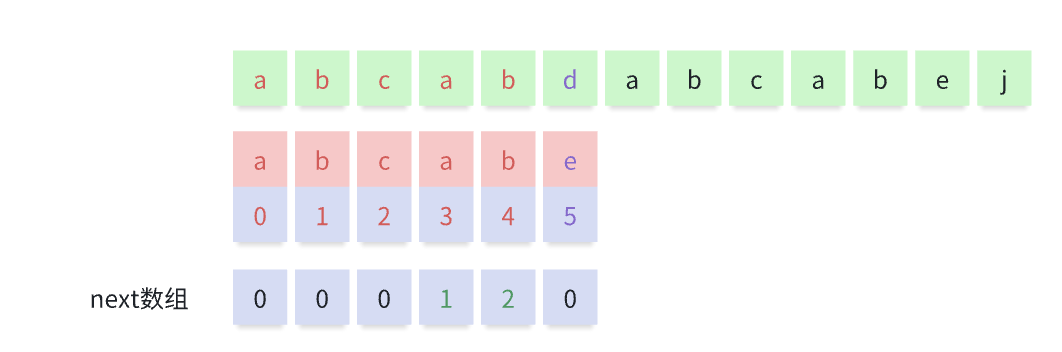
所以就可以忽略 下标 0、1， 从匹配串的下标2位置直接匹配, 至此，KMP的原理介绍完毕

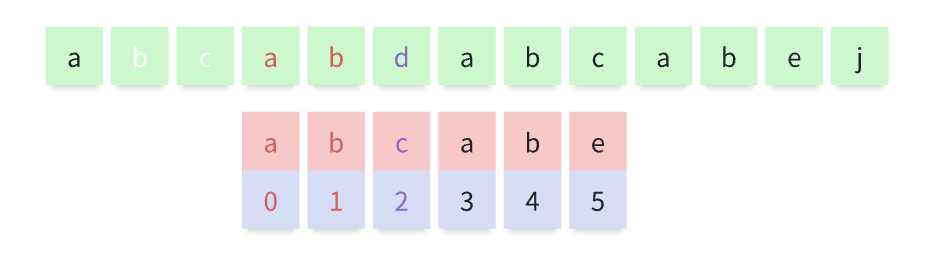
3. java代码实现

KMP算法中对于next数组构建的理解 - 驰 - 博客园 用的这位大佬的

3.1 next数组

private static int[] getNext(String patt){
        int len = patt.length();
        int[] next = new int[len];
        next[0] = 0;        // next数组的第一个元素肯定为0 
        int i = 1;          // next数组下标，0已固定，所以从next[1]开始求
        int prefix_len = 0; // 当前公共元素最大长度,也是前缀位置

        while(i < len){ // 循环求每个子串对应的prefix_len作为next数组
            if(patt.charAt(prefix_len) == patt.charAt(i)){  
                // 如果相等长度在上一次的基础上+1，就是当前next数组下标的公共元素最大长度
                // 比如：abcab 在第四位a时prefix_len为1，那在第5位b时一定是prefix_len+1=2
                prefix_len++;
                next[i] = prefix_len;
                i++;
            }
            else{ 
                 // 如果不相等,且最大长度为0，就可以直接设置next数组当前位为0,然后求下一个数组下标
                 // 相当于从第一位就没一致过 如  abcd  dcba
                if(prefix_len == 0){
                    next[i] = 0;
                    i++;
                }else{
                    // 这个不容易理解，后续会继续补充。为什么我们要回退到 next[prefix_len - 1]，再次循环i
                    //因为这个位置记录了之前已经匹配过的最长相同前后缀的长度。
                    // a b a b c  比如这个 在c处匹配失败，c是和第一个a比的，所以理论上第三位a也不用比，直接从第4位b比较 
                    prefix_len = next[prefix_len - 1];
                }
            }
        }

        return next;
    }

3.2 kmp遍历

private static int kmp(String s, String patt){
         // 获取next数组
        int[] next = getNext(patt)
        int len1 = s.length();
        int len2 = patt.length();
        int i = 0;  // 主串中的指针
        int j = 0;  // 子串中的指针

        // 主串一直增就行，靠子串的移动快速匹配
        while(i < len1){
             // 同时移动：如果主串第i个字符与子串第j个字符相等，则正常比较下一个字符  abcd abc
            if(s.charAt(i) == patt.charAt(j)){ 
                i++;
                j++;
            }
            // 移动子串：如果不相等且子串不在起始位置，则根据next数组移动子串指针  abcab  abf
            else if(j > 0){   
                j = next[j - 1];
            }else{ 
                 // 移动主串：如果不相等且子串在起始位置，那么主串移动到下一个位置   abcd  bac
                i++;
            }

            // 如果子串指针等于子串长度，说明匹配结束，返回起始位置
            if(j == len2){  
                return i - j;
            }
        }

        return -1;  // 匹配失败返回-1

    }