树状数组
树状数组
一、单点修改和区间查询
lowbit函数
\[lowbit(x)=x\&(-x)
\]
作用:得到 \(x\) 二进制最右侧的1。
如,\(x=(0010010011000)_2\) ,则 \(-x=x取反+1=(1101101101000)_2\) , \(x\&(-x)=(0000000001000)_2\) 。
原理
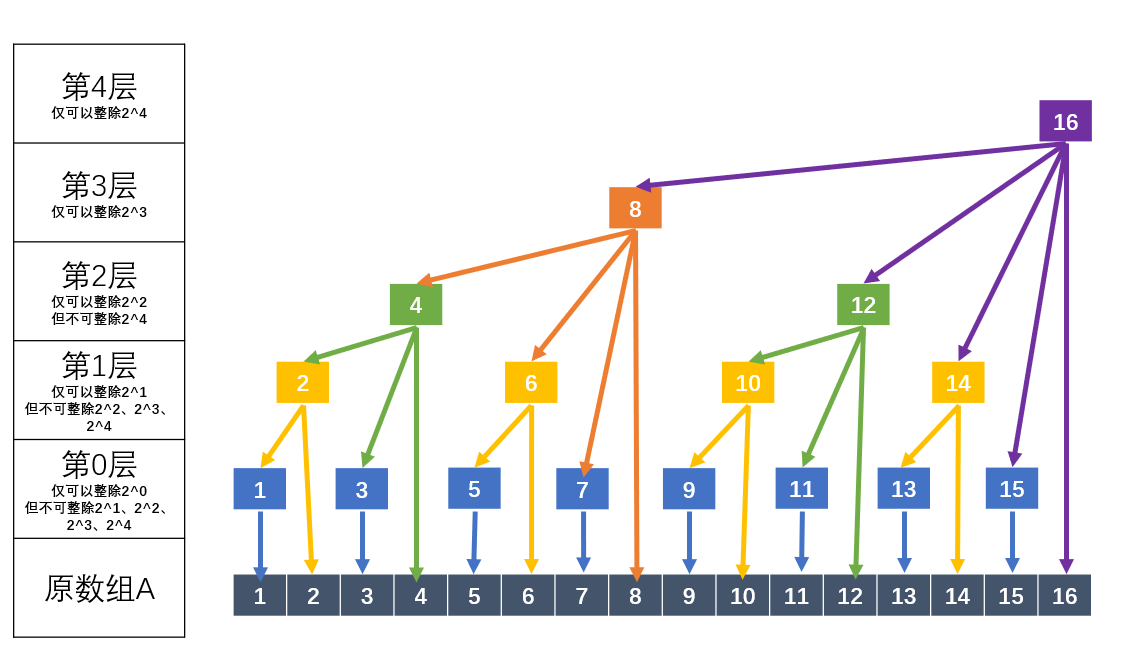
用 \(c[i]\) 表示树状数组,\(a[i]\) 表示原数组。
将 \(c[i]\) 中下标转为二进制后,定义 \(c[i]=a[i-lowbit(i)+1]+a[i-lowbit(i)+2]+...+a[i]\) 。
对于查询 \([L,R]\) ,利用前缀和想法将其拆为 \(\sum_{i=1}^{R}a_i-\sum_{i=1}^{L-1}a_i\) ,考虑求解 \(\sum_{i=1}^xa_i\) 。将 \(x\) 转为二进制,让 \(ans+=c[x]\) 即加上 \([x-lowbit(x)+1,x]\) 的值,并让 \(x-=lowbit(x)\) 。不断重复上述操作即可得到答案。
对于单点 \(x\) 位置的修改,发现x处的改动会影响 \(c[x+lowbit(x)]\) 的值,于是不断让 \(x+=lowbit(x)\) 修改 \(c[x]\) 处的值即可。
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int c[N],a,n,m;
int lowbit(int x){
return x&(-x);
}
void add(int x,int v){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=v;
}
}
int query(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)){
ans+=c[i];
}
return ans;
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i){
scanf("%d",&a);
add(i,a);
}
int opt,x,y;
while(m--){
scanf("%d %d %d",&opt,&x,&y);
if(opt==1) add(x,y);
else printf("%d\n",query(y)-query(x-1));
}
return 0;
}
二、区间修改和单点查询
利用差分与前缀和思想,考虑用树状数组维护差分数组 \(s[i]\) 。
对于修改 \([L,R]\) ,只需变为单点修改 \(s[L]\) 和 \(s[R+1]\) 即可。
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,m,a[N],c[N];
int lowbit(int x){
return x&(-x);
}
void add(int x,int v){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=v;
}
}
int query(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)){
ans+=c[i];
}
return ans;
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
}
int opt,x,y,k;
while(m--){
scanf("%d %d",&opt,&x);
if(opt==1){
scanf("%d %d",&y,&k);
add(x,k);
add(y+1,-k);
}
else{
printf("%d\n",a[x]+query(x));
}
}
return 0;
}
一些题目
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=5e5+5;
int n,a[N],c[N],s[N];
LL ans;
int lowbit(int x){
return x&(-x);
}
void add(int x){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]++;
}
}
int query(int x){
int cnt=0;
for(int i=x;i;i-=lowbit(i)){
cnt+=c[i];
}
return cnt;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
s[i]=a[i];
}
sort(s+1,s+1+n);
for(int i=1;i<=n;++i){
a[i]=lower_bound(s+1,s+n+1,a[i])-s;
ans+=(LL)i-1ll-(LL)query(a[i]);
add(a[i]);
}
printf("%lld",ans);
return 0;
}
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1e5+5;
int n,hd[N],tot,dfn[N],d[N],p[N],idx;
LL ans,c[N];
struct node{
int nxt,to;
}edge[N<<1];
void add_edge(int x,int y){
edge[++tot]=node{hd[x],y};
hd[x]=tot;
}
void dfs(int x,int fa){
dfn[x]=++idx;
for(int i=hd[x];i;i=edge[i].nxt){
int y=edge[i].to;
if(y==fa) continue;
dfs(y,x);
}
d[x]=idx;
}
int lowbit(int x){
return x&(-x);
}
void add(int x,LL v){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=v;
}
}
LL query(int x){
LL cnt=0;
for(int i=x;i;i-=lowbit(i)){
cnt+=c[i];
}
return cnt;
}
int main(){
scanf("%d",&n);
int x,y;
for(int i=1;i<n;++i){
scanf("%d %d",&x,&y);
add_edge(x,y);
add_edge(y,x);
}
dfs(1,1);
for(int i=1;i<=n;++i){
scanf("%d",&p[i]);
}
for(int i=1;i<=n;++i){
printf("%lld\n",query(dfn[p[i]]));
add(dfn[p[i]],1);
add(d[p[i]]+1,-1);
}
return 0;
}
#include <bits/stdc++.h>
#define mod 1000000009
using namespace std;
const int N=1e5+5;
int n,a[N],sum[N],dp[N],ans,c[N],tmp[N];
int lowbit(int x){
return x&(-x);
}
void add(int x,int v){
for(int i=x;i<=n+1;i+=lowbit(i)){
c[i]=(c[i]+v)%mod;
}
}
int query(int x){
int res=0;
for(int i=x;i;i-=lowbit(i)){
res=(res+c[i])%mod;
}
return res;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
tmp[i]=sum[i]=sum[i-1]+a[i];
}
sort(tmp,tmp+1+n);
for(int i=0;i<=n;++i){
sum[i]=lower_bound(tmp,tmp+n+1,sum[i])-tmp+1;
}
add(sum[0],1);
for(int i=1;i<=n;++i){
ans=query(sum[i]);
add(sum[i],ans);
}
printf("%d",ans%mod);
// dp[0]=1;
// for(int i=1;i<=n;++i){
// for(int j=0;j<i;++j){
// if(sum[i]-sum[j]>=0){
// dp[i]=(dp[i]+dp[j])%mod;
// }
// }
// }
// printf("%d",dp[n]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号