Python的MRO以及C3线性化算法
python3 中的方法解析顺序 (Method Resolution Order , MRO)采用C3线性化算法来确定
(百度Python MRO排在首位的文章，绝大部分内容是正确的，但是核心公式错了)
简而言之，一个类的MRO应当如下确定
L[object] = [object]
L[C(B1…BN)] = [C] + merge(L[B1]…L[BN], [B1, … ,BN])
这里的关键在于 merge，其输入是一组列表，按照如下方式输出一个列表：
- 检查第一个列表的头元素（如 L[B1] 的头），记作 H。
- 若 H 未出现在其它列表的尾部，则将其输出，并将其从所有列表中删除，然后回到步骤1；否则，取出下一个列表的头部记作 H，继续该步骤。
- 重复上述步骤，直至列表为空或者不能再找出可以输出的元素。如果是前一种情况，则算法结束；如果是后一种情况，说明无法构建继承关系，Python 会抛出异常。
示例1
继承关系如下图
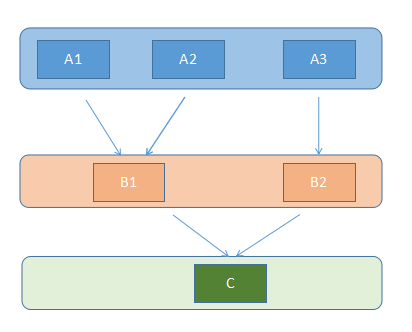
根据上述C3算法的步骤来计算其MRO
首先计算B1的MRO:
L[B1(A1,A2)] = [B1] + merge(L[A1], L(A2), [A1, A2])
= [B1] + merge([A1,Obj], [A2,Obj], [A1,A2])
= [B1, A1] + merge([Obj], [A2,Obj], [A2])
= [B1, A1, A2] + merge([Obj], [Obj])
= [B1, A1, A2, Obj]
同理,计算B2的MRO(过程略):
L[B2(A3)] = [B2, A3, Obj]
最终计算并得到C的MRO
L[C(B1,B2)] = [C] + merge(L[B1(A1,A2)], L[B2(A3)], [B1,B2])
= [C] + merge([B1, A1, A2, Obj], [B2, A3, Obj], [B1,B2])
= [C, B1] + merge([A1, A2, Obj], [B2, A3, Obj], [B2])
= [C, B1, A1] + merge([A2, Obj], [B2, A3, Obj], [B2])
= [C, B1, A1, A2] + merge([Obj], [B2, A3, Obj], [B2])
= [C, B1, A1, A2, B2] +merge([Obj], [A3, Obj])
= [C, B1, A1, A2, B2, A3] +merge([Obj], [Obj])
= [C, B1, A1, A2, B2, A3, Obj]
根据C3算法成功构建了MRO，所以这个类的继承关系是被允许的，而且根据MRO可以明确地指出应当如何去查找其父类的属性/方法。即按照MRO列表由前向后的顺序来查找。
当然，我们完全没有必要去计算这个序列，直接使用.mro()类方法即可查看该类的MRO
C.mro()
[<class '__main__.C'>, <class '__main__.B1'>, <class '__main__.A1'>, <class '__main__.A2'>, <class '__main__.B2'>, <class '__main__.A3'>, <class 'object'>]
与我们计算的结果是相同的。
正确理解MRO是使用多重继承和super()完成多继承类协作任务的基础。
