【二叉树】最近公共祖先

什么是最近公共祖先

Leetcode236. 二叉树的最近公共祖先
“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
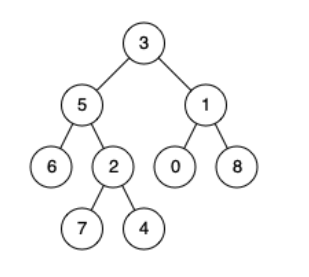
以下图为例：

• 5 1 的公共祖先是 3
• 5 2 的公共祖先是 5
  

思路

给定根节点root, 两个节点 p、q，p和q的分布有两种情况：

• p、q 都在root的一边
• p在root的一边, q在root另一边

于是乎，可以从根节点遍历，递归向左右子树查询节点信息

• root为空，只能返回 nullptr 也就是 root
• root等于p、q中的任一个，满足了上面的定义一个节点也可以是它自己的祖先，也直接返回 root
• p、q 在root的两边，root就是p和q的公共祖先，返回root
• p、q 在root的一边，那就返回 left 或者 right

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root || root == p || root == q) return root;
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if (left && right) return root;
        return left ? left : right;
    }
};

复杂度分析

时间复杂度：O(N)，其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次，因此时间复杂度为 O(N)。

空间复杂度：O(N) ，其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为 N，因此空间复杂度为 O(N)。

---

再来一题

Leetcode235. 二叉搜索树的最近公共祖先

二叉搜索树相比于普通的二叉树又多了一个条件：对应节点的值 左 < 根 < 右
多了个条件，那一般就能再优化，既然知道了 左 根 右 的大小关系，那就能很容易的判断出p、q在root的哪一边

class Solution {
public:

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(!root || root==p || root==q) return root;
        //q、q都在左
        if(root->val > p->val && root->val > q->val){
            return lowestCommonAncestor(root->left, p, q);
        }
        //q、q都在右
        if(root->val < p->val && root->val < q->val){
            return lowestCommonAncestor(root->right, p, q);
        }
        return root;
    }
};