【2016级学长的邀请赛】Problem A 空門蒼的睡梦
Description
空門蒼的爱好就是睡觉,无论在岛上的哪个角落都有可能看到她的睡姿,你一定很好奇她是怎么完成作业的吧!当然是请人帮她完成啦!如此可爱的她,怎么可能会有人拒绝帮助她完成作业呢?
我一直都,能听到你的声音。
那些声音,让我感到无比安心。
它们是如此的柔软,又是如此的温和,就像是那催促着人们醒来的清晨的阳光一样。
那是我最喜欢的声音。
我不自觉地,就露出了微笑。
虽然,身体还稍微有点没法自由地行动……
但是,温柔又耀眼的光芒,还是摇动了我的内心。
感觉呼吸变得稍微有点局促。
如同波纹一样……
又如同心跳一般……
我能感受到,有一股暖流,正在我的体内流动着。
就这样,我毫不犹豫地张开了嘴巴。
因为,我已经很清楚了,很清楚在最开始的时候应该说些什么。
那是我一直都在说的话。
同时,也是我一直都很想说的话。
空門蒼今天的作业是这样的:
有n个不同的奇数,m个不同的偶数,它们构成的集合元素个数为 (n+m),
那么这个集合的所有子集中有多少个满足奇数个数大于偶数个数。
现在空門蒼再次陷入沉睡,她希望你能够在她醒来之前完成作业,这将是她睡梦中最美好的记忆。聪明的你能够帮助她吗?
由于答案很大,你只需要对 1e9+7 取模即可。
Input
一行两个整数表示 n,m 。(意义见题目描述)
Output
一个数表示答案(对 1e9+7 取模)
Sample Input
5 8
Sample Output
1093
Hint
对于20%数据,1<=n,m<=20
对于60%数据,1<=n,m<=5000
对于100%数据,1<=n,m<=1e7
对没错,这是一道数论题
前置姿势:组合数
感谢 @dust姐姐 @软白姐姐 提供姿势支持qwq
百科的定义:
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。
计算方式如下:
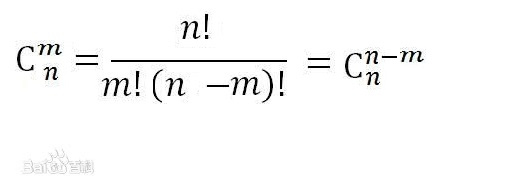
那么我们就可以轻松地用C++实现它(递推写法):
int C(int n, int m)
{
if (n == m || m == 0) return 1;
return C(n-1, m) + C(n-1, m-1);
}
但是计算组合数最大的困难在于数据的溢出,对于大于150的整数n求阶乘很容易超出double类型的范围。
那么当C(n,m)中的n=200时,直接用组合公式计算基本就无望了。
另外一个难点就是效率。
像我这种彩笔一看就不会组合数(其实是因为高一还没学)
以下是正经题解
观察一下题目:
求集合的所有子集中有多少个满足奇数个数大于偶数个数。
记已选的奇数个数为x
记已选的偶数个数为y
假设已经选了y个偶数
此时有 C(y,m) 种
那么当 x > y 时
得到的就是 $$ C(y, m)\sum_{i=y+1}^{n} C(i, n) $$
对于每个可能的y:
都去求有多少种情况,就不会重复
所以可以轻易推出答案为:
其中
- 代表从m个偶数中选y个
- 处理对于一个定值y求合法集合的数量
Example:
要从集合中选y个偶数
令 res = C(y, m)
那么选 y + 1, y + 2, ... y + n个偶数也符合条件
则有 res = C(y, m)(C(y+1, n) + C(y+2, n) + ... + C(n, n))
那现在就开始切这题吧!
先来一波谁都懂的开头:
#include <bits/stdc++.h>
const int Maxn = 1e7 + 10;
const int Mod = 1e9 + 7;
using namespace std;
typedef unsigned long long ull;
ull fact[Maxn], inv[Maxn];
再来写个求C(m, n) 和 预处理函数
ull C(ull n, ull m)
{
return (fact[n] * inv[n - m] % Mod) * inv[m] % Mod;
}
inline void pre(ull n)
{
fact[0] = 1;
for(ull i = 1; i <= n; i++)
fact[i] = fact[i - 1] * i % Mod;
inv[1] = 1;
for(ull i = 2; i <= n; i++)
inv[i] = (Mod - Mod / i) * inv[Mod % i] % Mod;
inv[0] = 1;
for(ull i = 1; i <= n; i++)
inv[i] = inv[i] * inv[i - 1] % Mod;
}
然后愉快的计算
ull su[Maxn];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
pre(Maxn);
ull n, m;
cin >> n >> m;
su[0] = 1;
for(ull i = 1; i <= n; i++)
{
su[i] = su[i - 1] + C(m, i);
su[i] %= Mod;
}
ull ans = 0, res;
for(ull i = 1; i <= n; i++)
{
res = 0;
if(i - 1 <= m)
res = su[i - 1] % Mod;
else
res = su[m] % Mod ;
res = res * C(n, i) % Mod;
ans = ans % Mod + res % Mod;
}
cout << ans % Mod << "\n";
return 0;
}
测试一下,没有问题
到此 我们只用了30分钟就写完了一道题
愉快提交:
好家伙,TLE了
果然我太菜了
如何优化此代码?
这时候又要普及新姿势惹qwq
快速幂
(以下知识来源:百度百科)
顾名思义,快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高。
快速幂算法的核心思想就是每一步都把指数分成两半,而相应的底数做平方运算。
这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小,而最后表示的结果却一直不会变。
- 如何实现它呢?
先看一个简单的求\(a^b\)的函数
int _pow(int a,int b)
{
int ans = 1;
while(b--)
{
ans *= a;
}
return ans;
}
这个算法的复杂度是O(n)级别,咋一看好像很快
但是往往在比赛、做题的时候都需要处理指数很大运算,例如 210000000
你这要是不TLE(或者WA)我mitruha就直接扮成兽娘做你宠物
快速幂算法的原理是通过将指数拆分成几个因数相乘的形式,来简化幂运算。
Example:
在我们计算 313 的时候,普通的幂运算算法需要计算13次。
但是如果我们将它拆分成 3(8+4+1),再进一步拆分成 38 * 34* 31 只需要计算4次。
- 为什么要拆成3(8+4+1)? 我拆成3(9+3+1)不行吗?
把13转二进制,你会发现答案是1101
可以知道:13 = 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = 8+4+1
所以就根据这种思路,我们可以写出快速幂的代码了:
inline ll ksm(ll a,ll b) {
ll s = 1,base = a;
for (;b;b >>= 1,base = base * base % mod)
if (b & 1)
s = s * base % mod;
return s;
}
AC代码如下:(tjx yyds)
// Date : 2018-10-10 17:09:41
// Author : tjx
// problem :
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#define MAXN 10000005
#ifdef WIN32
#define LL "%I64d"
#else
#define LL "%lld"
#endif
using namespace std ;
typedef long long ll;
const ll mod = ll(1e9 + 7);
inline bool isdigit(char& ch) {
return ch >= '0' && ch <= '9';
}
inline ll read() {
ll s = 0,f = 1;char ch = getchar();
for (;!isdigit(ch);ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch);ch = getchar())
s = (s << 1) + (s << 3) + ch - '0';
return s * f;
}
inline void write(ll x) {
if (x == 0) {putchar('0');return ;}
if (x < 0) {putchar('-');x = -x;}
int _stk[65],_top = 0;
for (;x;x /= 10) _stk[++_top] = x % 10 + 48;
for (;_top;_top--)putchar(_stk[_top]);
}
int n,m;
ll fac[MAXN],p[MAXN];
ll f,g;
inline ll ksm(ll a,ll b) {
ll s = 1,base = a;
for (;b;b >>= 1,base = base * base % mod)
if (b & 1)
s = s * base % mod;
return s;
}
/*
k! = (k - 1)! * k (mod m)
(k - 1)! ^ -1 = k! ^ -1 * k (mod m)
*/
void premake(int M) {
fac[0] = 1;
for (int i = 1;i <= M; ++i)
fac[i] = fac[i - 1] * i % mod;
p[M] = ksm(fac[M],mod-2);
for (int i = M;i >= 2; --i)
p[i - 1] = p[i] * i % mod;
p[0] = p[1] = 1;
}
// C(n,m) = n! / (n - m) ! / m!
inline ll C(int i,int j) {
return (fac[i] * p[i - j] % mod) * p[j] % mod;
}
int main () {
n = read();m = read();
premake(max(n,m));
f = g = 0;
for (int i = 1;i <= n; ++i) {
if (i - 1 <= m) {
g = (g + C(m,i - 1));
g = g >= mod ? g - mod : g;
}
f = f + (C(n,i) * g) % mod;
f = f >= mod ? f - mod : f;
}
write(f);
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号