前言
此篇文章用于介绍分类问题。利用机器学习进行分类的例子有垃圾邮件识别(iOS端的熊猫吃短信估计就是用的这个技术,我现在还一直在用),网上交易,肿瘤分类等。在篇一内已经详细的说明了线性回归和它的工作原理,线性回归主要进行的工作就是一个拟合的过程,在拟合过程中利用梯度下降方法使得拟合误差最小。那么在分类问题中,若使用线性回归进行处理显然是不够准确的,这个时候就应当使用下面介绍的逻辑回归(Logistic回归)处理分类工作。
通常把0称为负类,1称为正类,在正负类的规定上并没有强制要求。
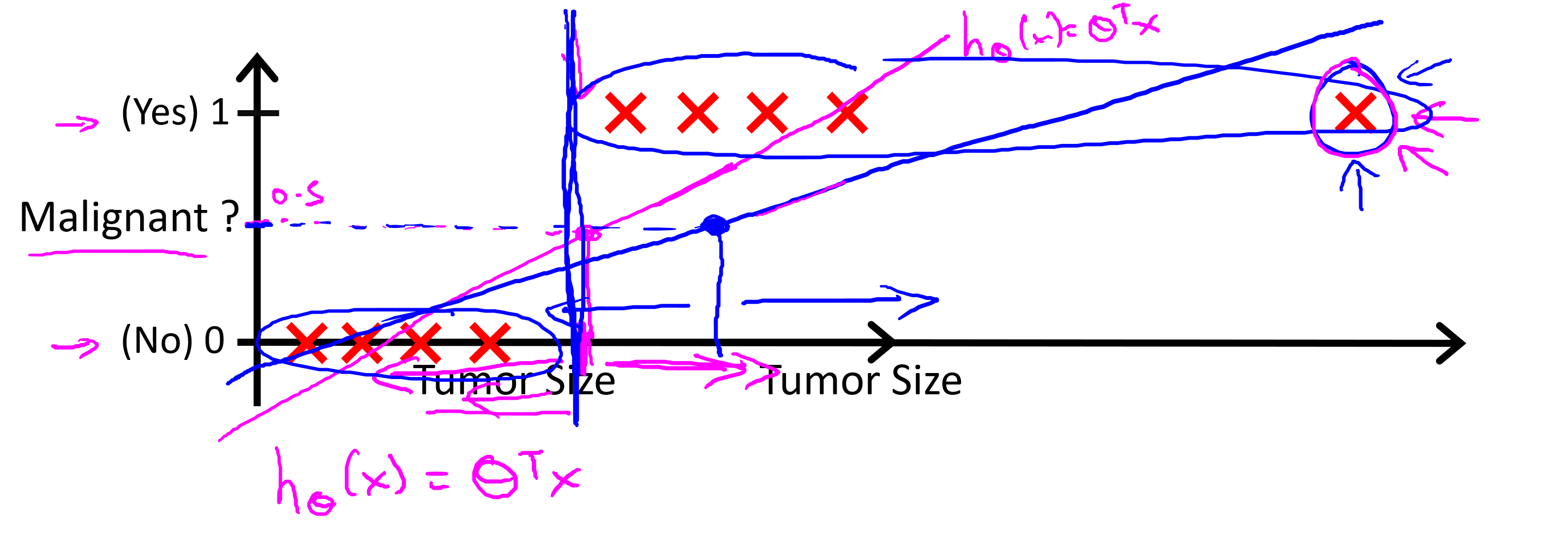
上图中可以看出在最右侧增加了一个肿瘤样本之后,导致了线性回归模型变化(红色->蓝色),红色的回归模型还算是可以应用到此场景下的分类问题,但是增加了肿瘤样本之后的蓝色回归模型并不能够再适用于这个问题,所以使用线性回归处理分类问题并不是一个好的方法。
线性回归模型的结果是任意的实数,逻辑回归模型的结果处于0~1之间,这样应用于分类问题更佳完美。可以将逻辑回归H(x)理解为对于给定的输入x,使得y=1的概率估计。
逻辑回归
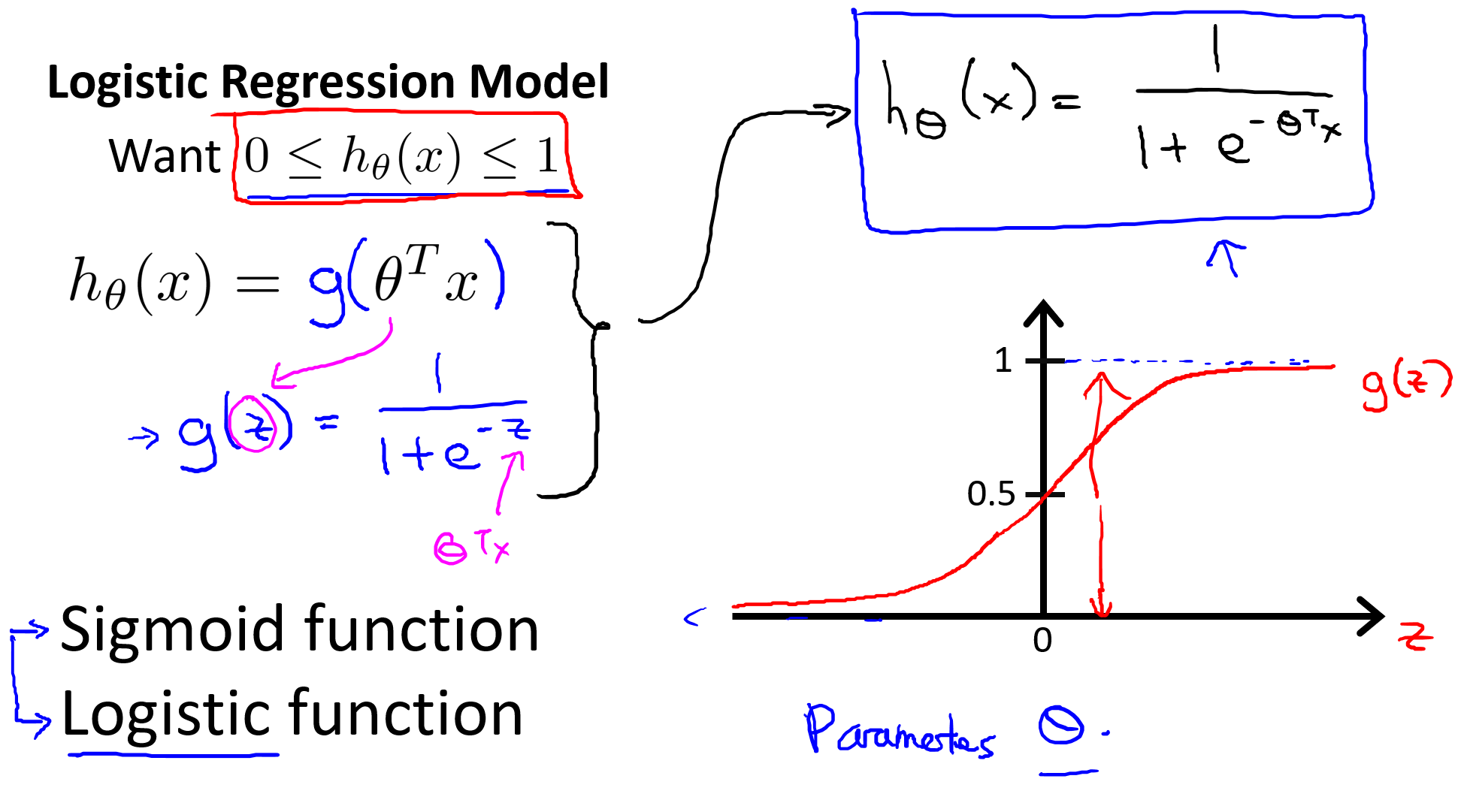
逻辑回归模型
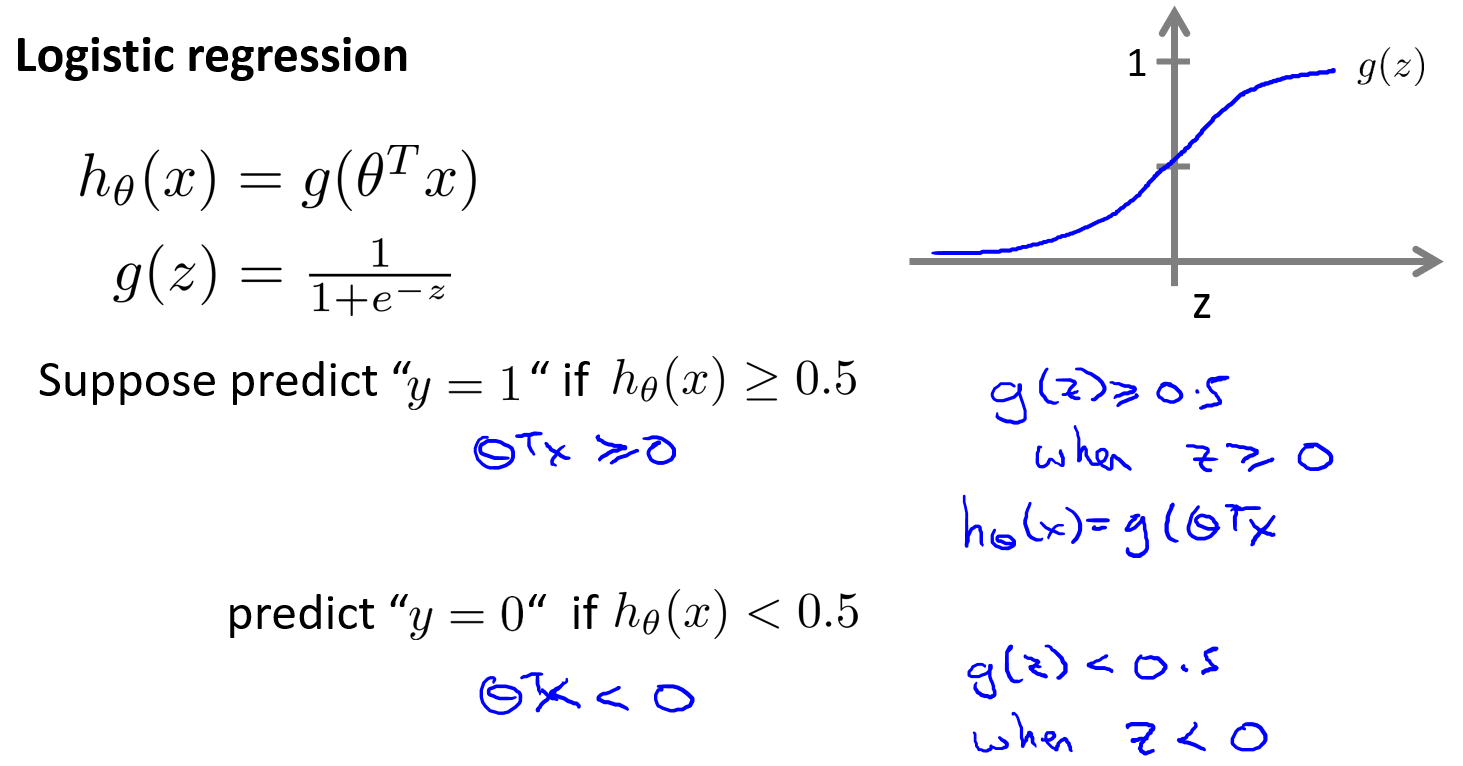
Logistic regression
这里把g(z)函数称为
逻辑函数或者sigmoid函数,这两个表述是一致的。
逻辑回归公式如下:
$$h_θ(x)=\frac{1}{1+e^{-θ^Tx}}$$
对逻辑回归模型通俗的解释一下,h
θ(x)的输出值就是在给定输入x的情况下,使得y=1的概率估计。
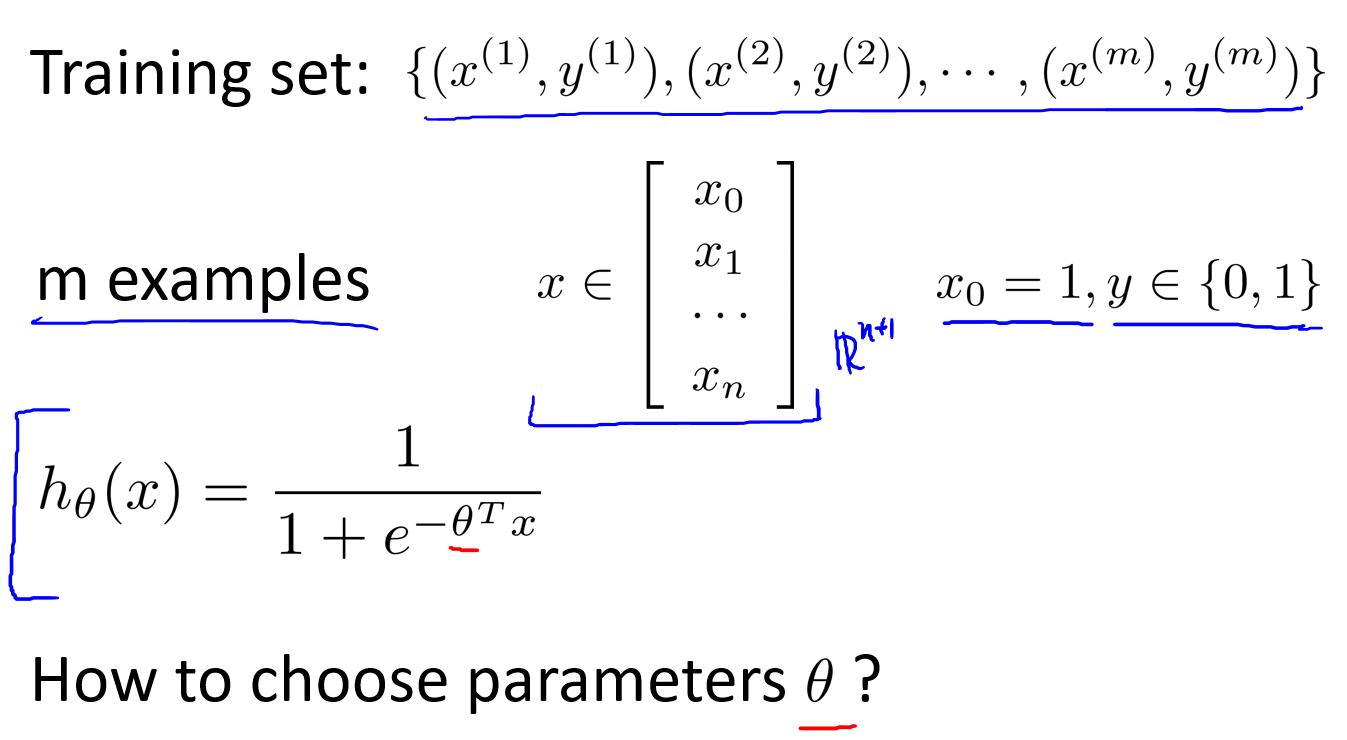
上图中的x
0总是等于1的,另一个特征是x
1,其含义也就是肿瘤的大小。
h
θ(x)代表着,在给定的x和θ情况下,y=1的概率是0.7。
决策边界
decision boundary
只要θTx≥0,那么hθ(x)≥0.5,即可推出y=1。
下面利用具体示例阐述上面蓝色加粗字体。
图中的决策边界实际上是根据θ
Tx=0画出来的,因为当θ
Tx>0的时候,也就是测试点刚好落到边界附近,那么此时使得y=1的概率估计应当稍微大于0.5。
当θ
Tx远远大于0的时候,也就是测试点远离边界附近,那么这个时候测试点有很大的概率使得y=1,也就是y=1的概率估计应当接近1。
通过增加复杂的多项式,可以得到
**更复杂的决策边界**。在增加多项式的时候可以是对原有特征的平方或者三次方等。
代价函数2
cost function
无论是线性回归,还是逻辑回归,均离不开对模型参数的选择。在线性回归可以使用梯度下降,每次通过更新模型参数降低cost值来得到最优的模型参数,那么在逻辑回归中又该怎样设计cost函数呢?
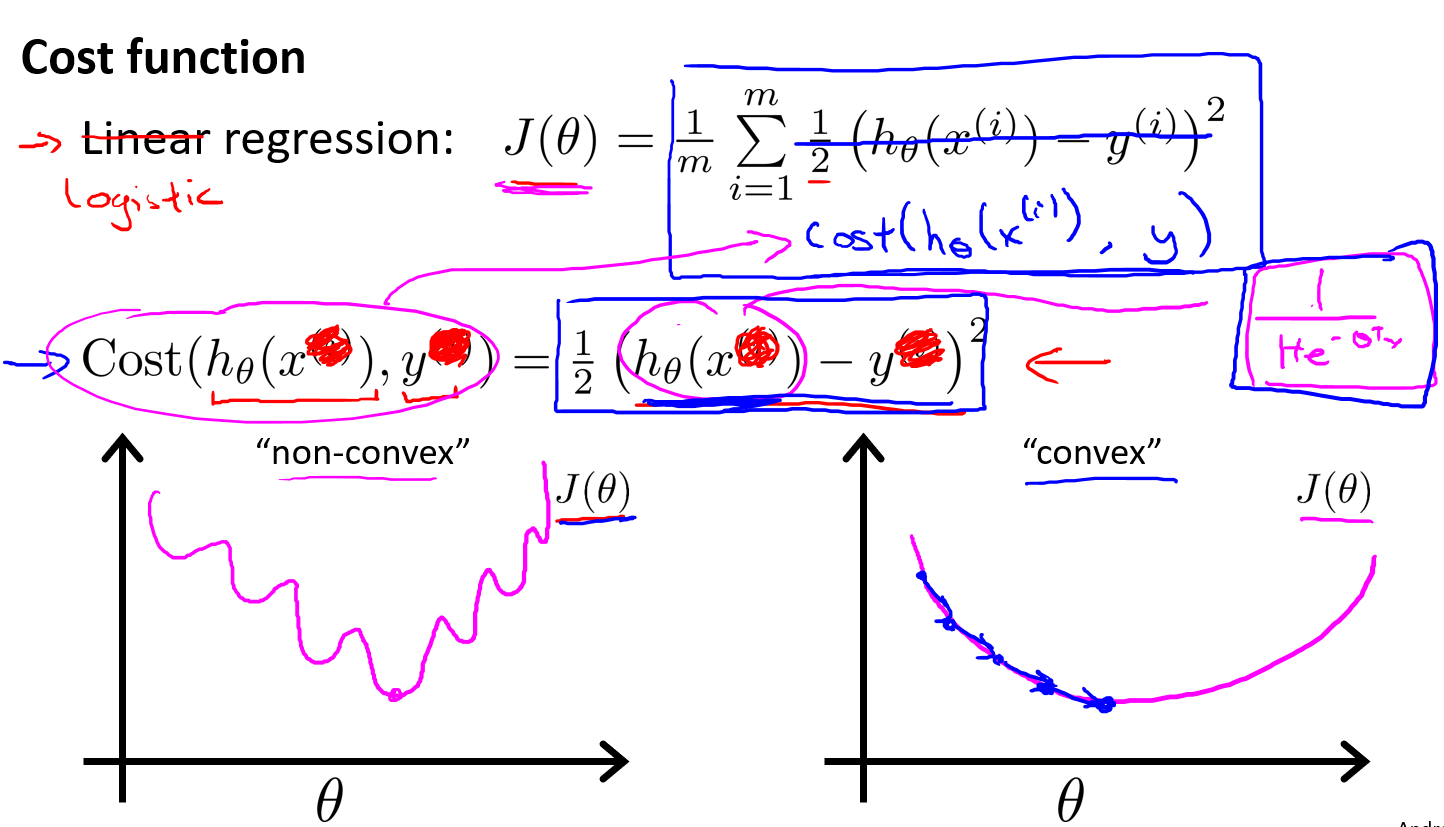
首先尝试一下逻辑回归是否可以直接挪用线性回归的代价函数公式,经过实验可以发现,**
若逻辑回归采用和线性回归同样的公式的话,会导致代价函数成为一个非凸函数(non-convex)**,具体关于非凸函数的定义前面应当已经介绍过了。这类函数图像不利于梯度下降进行正常工作,我们希望得到的Cost函数是上图右侧的图像。
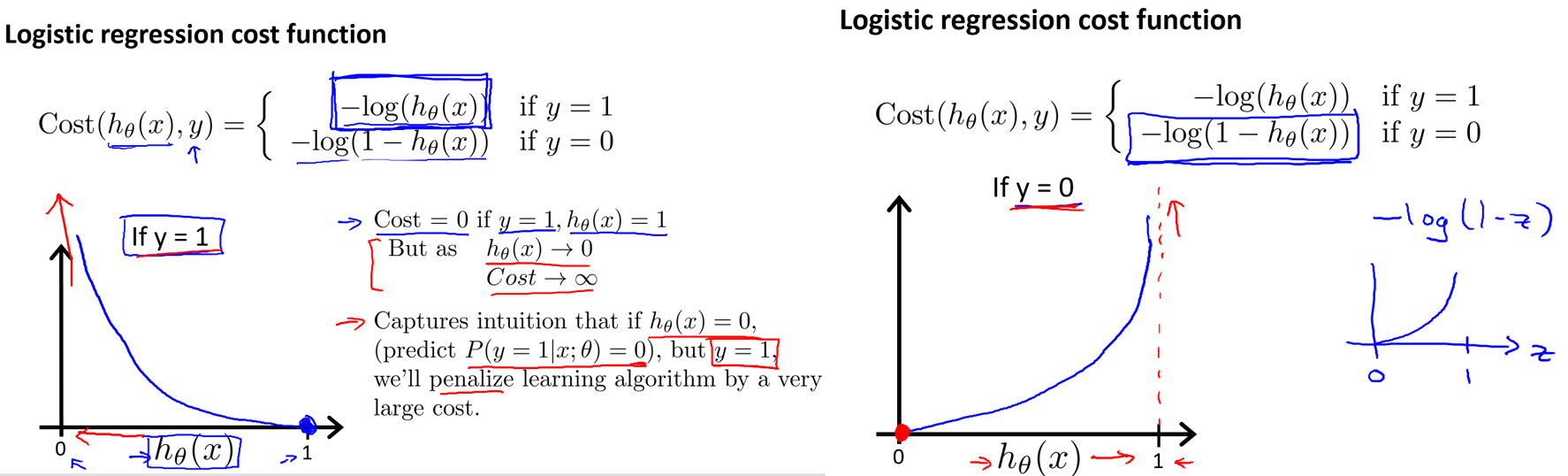
逻辑回归代价函数Cost Function公式定义如下:
\[Cost(h_θ(x),y)=\begin{cases}-log(h_θ(x)){\quad}{\quad}{\quad}if{\,} y=1 \\ -log(1-h_θ(x)){\quad}{\,}{\,}if {\,}y=0\end{cases}
\]
上图定义并介绍了逻辑回归的代价函数,别忘了代价函数的值越高,说明当前模型参数的惩罚力度越需要加大。
左图:如果模型在给定一个样本和特定模型参数的情况下最后的计算结果是hθ(x)=0,但是此样本点y实际上=1,那么这个模型参数很显然需要接受惩罚,因此它的代价值是无穷大的。若此模型结果hθ(x)=1,刚好样本点也为1,那么这个模型参数是正好拟合了这个样本点,就不需要接受任何惩罚,因此它的代价值是等于0的。
右图:与左图是相同的道理,如果模型计算值与实际样本值是相同的,那么代价值就是0,如果模型计算值与样本值是相反的,那么代价值就是无穷大。
总结:利用这种代价函数可以得到凸函数图像(convex),凸函数图像方便梯度下降工作。(这样的话就能得到一个最优解,否则对于非凸函数图像来说会有无数个局部最优解,且难以利用梯度下降正常工作)
简化代价函数
Cost Function
上面介绍了原版的逻辑回归代价函数,当要将它使用到梯度下降时,如果还分两种情况就会得到两个梯度下降的公式,这样以来程序设计就会变得麻烦,不如先将代价函数进行化简,化简称为一个函数之后就可以直接用梯度下降了。下面是代价函数化简流程:
\[J(θ)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_θ(x^{(i)},y^{(i)}))
\]
\[Cost(h_θ(x),y)=\begin{cases}-log(h_θ(x)){\quad}{\quad}{\quad}if{\,} y=1 \\ -log(1-h_θ(x)){\quad}{\,}{\,}if{\,} y=0\end{cases}
\]
\[Note: y=0{\quad}or{\quad}1{\quad}always
\]
上述第二行Cost(hθ(x),y)可以转换成下面的形式(将y=1和y=0的两种情况合并在一起):
\[Cost(h_θ(x),y)=-y·log(h_θ(x))-(1-y)·log(1-h_θ(x))
\]
将化简后的Cost(hθ(x),y)代入到J(θ)内
\[J(θ)=-\frac{1}{m}·[{\,}\sum_{i=1}^{m}y^{(i)}log({\,}h_θ(x^{(i)}){\,})+(1-y^{(i)})log({\,}1-h_θ(x^{(i)}){\,}){\,}]
\]
上面的J(θ)其实本质是使用极大似然估计得到的。
梯度下降
Gradient Descent
\[J(θ)=-\frac{1}{m}·[{\,}\sum_{i=1}^{m}y^{(i)}log({\,}h_θ(x^{(i)}){\,})+(1-y^{(i)})log({\,}1-h_θ(x^{(i)}){\,}){\,}]
\]
\[\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)
\]
\[θ_j:=θ_j-α\sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}
\]
可以看出,这里化简之后的梯度下降和之前的线性回归的梯度下降是一样的,只是这里的假设函数发生了变化。另外仍需要注意的是,一定要同步更新所有的thetaj。
高级优化
Optimization algorithm
红色框住的这部分算法比较的复杂,但是有点有很多,一般在octave中会有这些函数库,可以直接进行调用。
下面具体介绍了如何去使用高级优化算法。
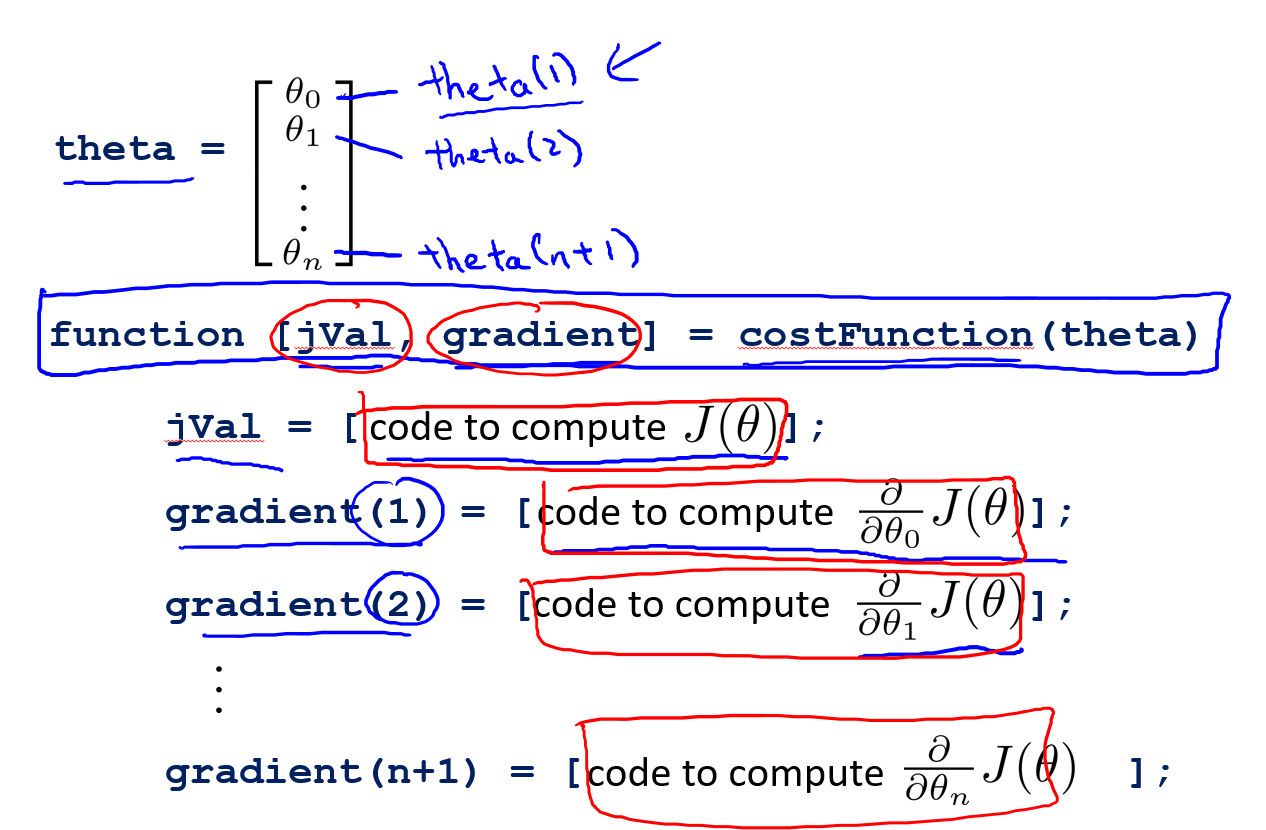
上图J(θ)是随意假设出来的一个特定公式,右上侧定义了
**costFunction(theta)**函数,这个函数能够返回以下两项内容:
- **
jVal:jVal实际上是计算J(θ)的公式,可以将其看成是代价公式**
- **
gradient:gradient是一个n维度向量(n=参数数目+1),由J(θ)对每个theta
j的偏导项构成**
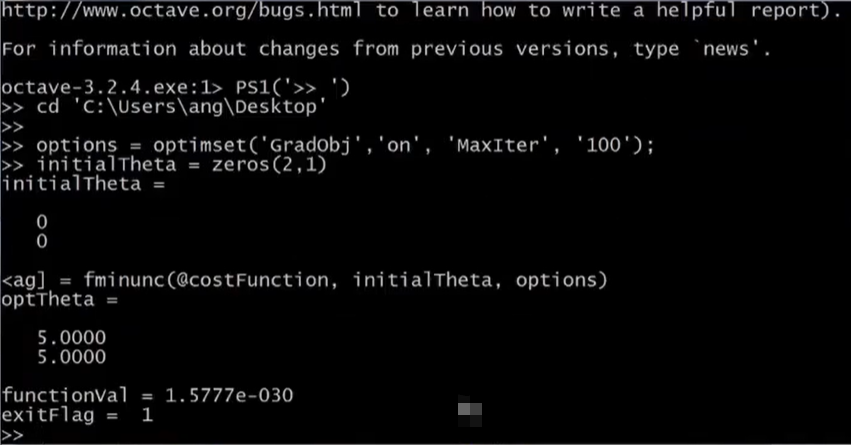
上图最后一部分蓝色的代码是**
调用高级优化函数的代码段**,需要注意的是,这里的initialTheta必须是2维或者2维以上的向量,如果是1维的话,fminunc很有可能无法运算。
functionVal表示的是最后的cost值,图中大概是10的-30次方,Exitflag表示当前已经收敛,optTheta内存储最后得到的模型参数。
在使用高级优化算法的时候,自己需要动手写代码的就是上图计算cost的公式以及梯度偏导项的gradient向量,写完了这些直接调用高级优化算法即可。
多类别分类
Multiclass classification
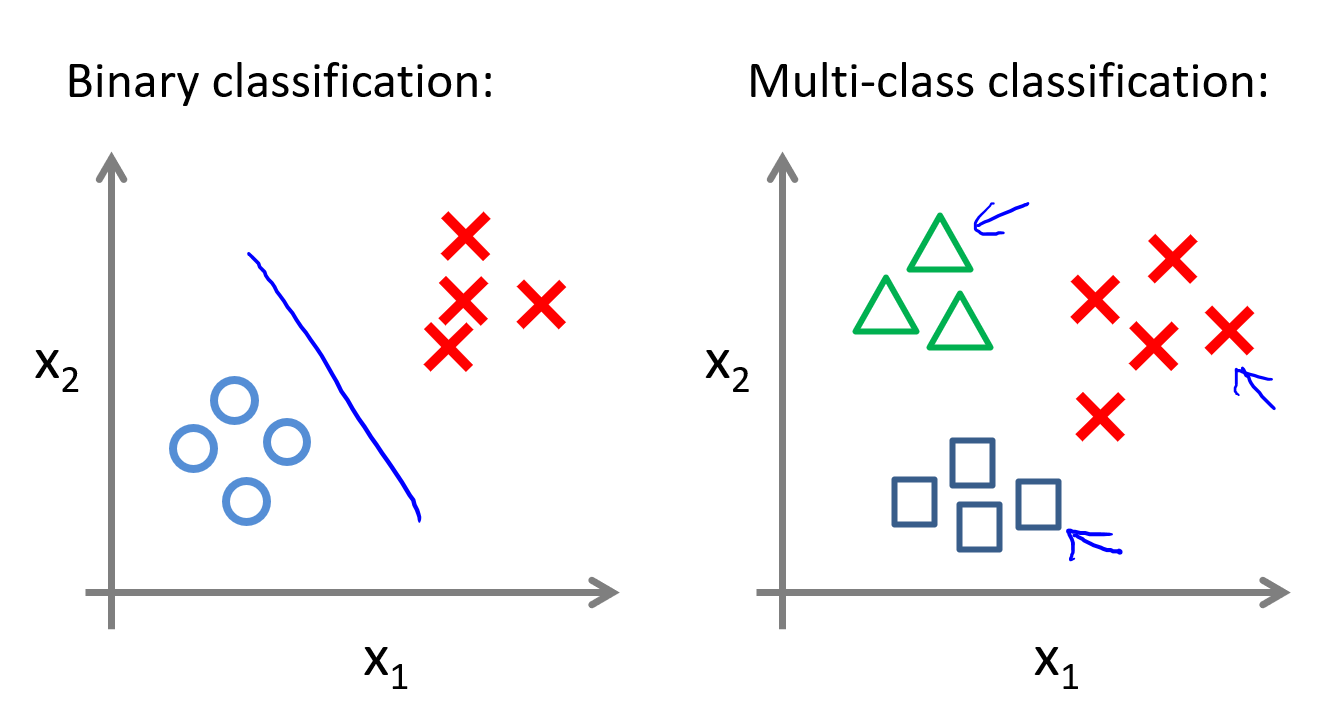
上图左侧是两个类别的标准分类,右侧是多类别分类。一般在进行天气预测(Sunny,Cloudy,Rain,Snow)的时候都是进行的多类别分类。
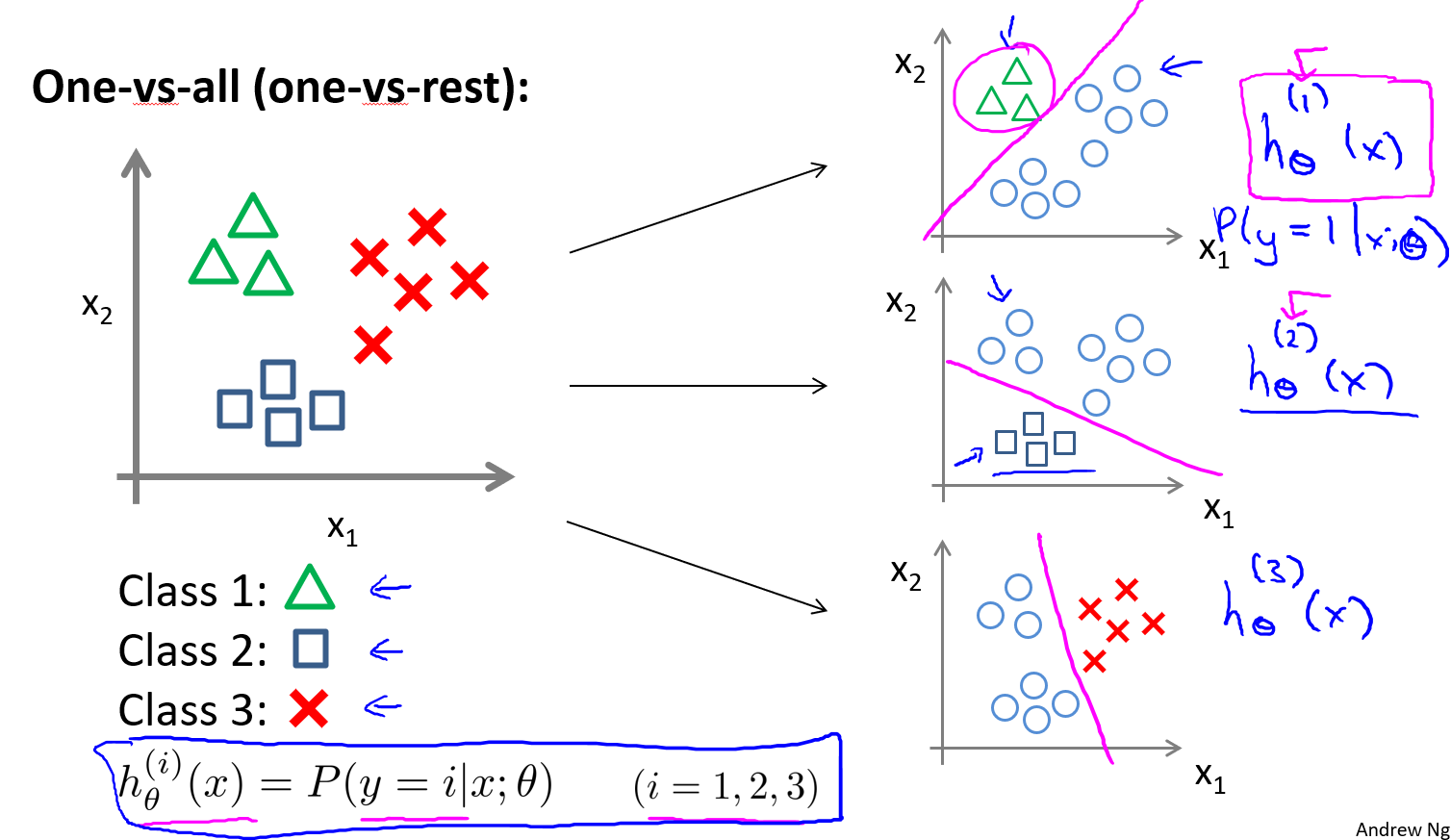
上图可以看出多类别分类的思想,也就是利用某一类和其余所有类别进行双类别分类,对每个类别都去训练一个逻辑回归分类器,然后这个时候要是需要判断一个新的样本的类别,就把这个类别x输入到所有的分类器当中,取概率最大的那个即可。下图删除了刚刚这段话介绍的内容:
过拟合问题
Overfitting
可以利用正则化减少过拟合问题
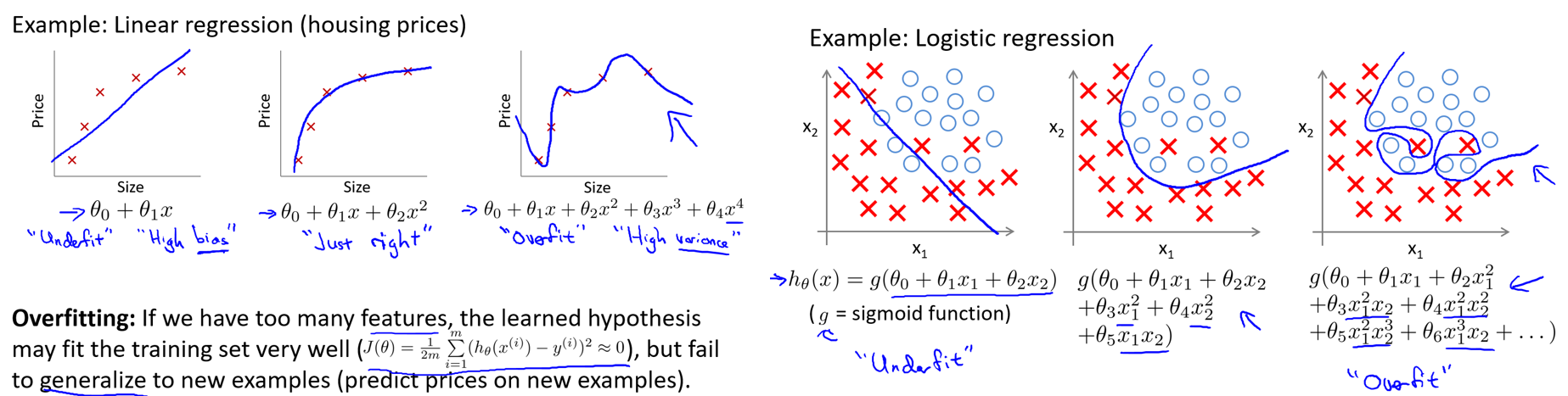
上图对应的三种状态分别是:1.欠拟合、2.正常拟合、3.过拟合。过拟合实际上是模型在很好的拟合数据集的情况下,对新样本的泛化能力严重不足的表现。也就是虽然模型在数据集上表现得非常优异,但是一旦应用到其它样本,那么这个时候模型代价就会非常高,说明模型的泛化能力非常差。
当特征过多,但是数据集样本非常少的时候,就非常容易发生过拟合的问题,一般可以使用两个方法缓解过拟合问题:
- 1.尝试减少选取特征变量的数量(人工检查法、模型选择法(后面的课程会介绍))
- 2.利用正则化(能够保留所有的特征,但是会减小模型参数的量级),即使有非常多的特征,使用正则化也能够非常好的进行预测工作。
正则化for costfunc
Regularization for cost function
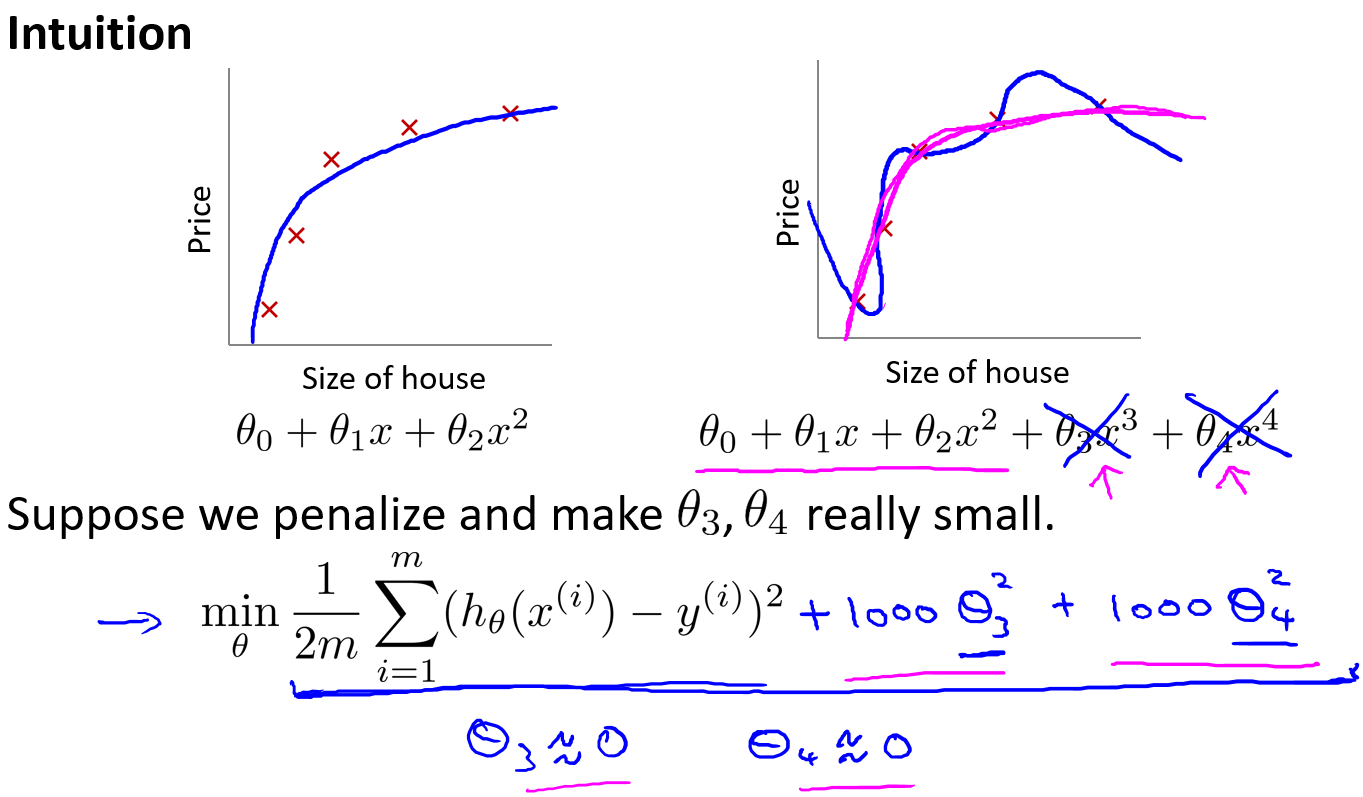
上图解释了正则化背后的思想,加入了θ
3和θ
4**
惩罚项**,这样为了保证得到最小的代价值,θ
3和θ
4必须很小才能够使得函数达到预期的效果,这样也就达到了我们的目的----即减小theta的大小。













 浙公网安备 33010602011771号
浙公网安备 33010602011771号