数据结构学习——串的模式匹配KMP算法

KMP算法

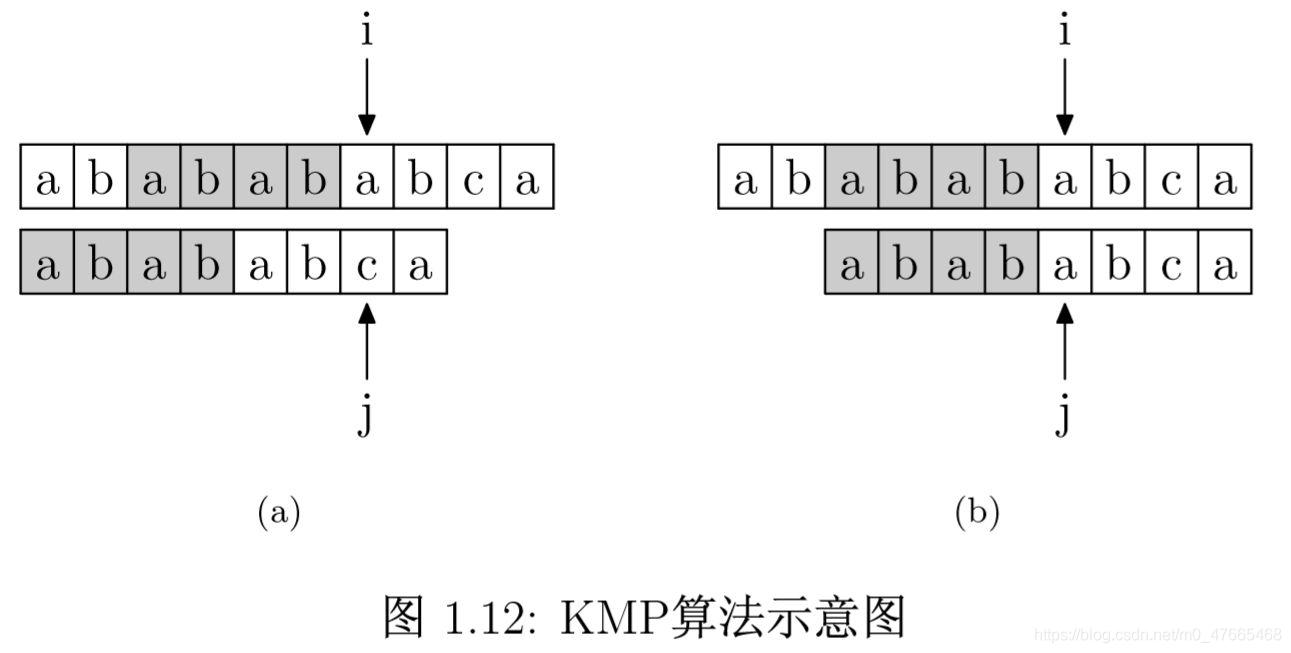
KMP算法是对BF算法的进一步改进，当匹配字符不相等时不需要回溯i指针 只需要滑动子串移动j的位置，匹配时仅需从模式串中第K个字符与第i个字符开始依次向后比较,那如何确定模式串j中开始匹配的第K个字符的位置呢

令\(next[j]=k\)，则\(next[j]\)表明当模式中第j个字符与字符中相应字符不匹配时，在模式中需要重新和主串中该字符进行比较的字符的位置。
S是主串 T是模式串
模式串的next函数的定义：

1. \(next[j]\)=0 j=1 (默认next[j]的第一位是0)
2. \(next[j]\)=MAX { (\(k| 1<k<j\) 且判断 模式串的前缀和后缀相等的个数有多少(N)， 则K-1=N，由此得K值,则\(next[j]=k\)}
3. \(next[j]\)=1 {K=1（当不存在相同子串时，进行下一步比较，这就属于其他情况K值等于1）}
   （////小白刚上手写个导图的样式也不太容易啊，呜呜呜呜呜呜）

\(nextval[j]\)修正函数值求解

      ////KMP算法
       int index_KMP(SString S,SString T,int pos)   ///S是主串 T是模式串
                         { //利用模式串T的next函数求T在主串S中第POS个字符之后的位置
                              //其中，T非空，1<=pos<=S.lengh
                              i=pos; j=1;   //初始化
                             while(i<=S.length && j<=T.length)  //两个串均未比较到串尾
                                { 
                                    if(S.ch[i]==T.ch[j]) 
                                       {++i;++j;} //继续比较后继字符
                                    else {
                                       j=next[j]; }       ///主串i不变，模式串j后退即模式串右移 
                                    }      
                             if(j>T.length)  return i-T.length; ///匹配成功
                                 else return 0;  //匹配失败 }