Elementary Sorts
初级排序
rules of the game
排序是很常见的需求,把数字从小到大排,把字符串按字典序排等等,目标是能对任何类型的数据进行排序,这可以通过回调(callback)实现:

Java 用接口实现回调,具体来说是可比较接口(Comparable),里面有个方法 compareTo(),大于小于等于分别返回 +1,-1 和 0,sort() 即调用这个方法来比较数据大小,不同类型数据的 compareTo() 可能不同,但 sort() 不用管这些,如下示例。
// Comparable interface(built in to Java)
public interface Comparable<Item> {
public int compareTo(Item that) {
// ...
return -1; // less
// ...
return +1; // greater
// ...
return 0; // equal
}
}
// sort implementation
public static void sort(Comparable[] a) {
int N = a.length;
for (int i = 0; i < N; i++)
for (int j = i; j > 0; j--)
if (a[j].compareTo(a[j - 1]) < 0)
exch(a, j, j - 1);
else break;
}
上面 sort() 不依赖于数组 a 的实际数据类型,只要 a 实现了可比较接口,就可以对其排序,实现了对不同类型数据排序的目标。Java 内置的类型,像 Integer,Double,String,Data 等,都实现了可比较接口,用户也可以很容易地对自己的数据类型实现可比较接口,例:
public class Date implements Comparable<Date> {
private final int month, day, year;
public Date(int m, int d, int y) {
month = m;
day = d;
year = y;
}
public int compareTo(Data that) {
if (this.year < that.year) return -1;
if (this.year > that.year) return +1;
if (this.month < that.month) return -1;
if (this.month > that.month) return +1;
if (this.day < that.day) return -1;
if (this.day > that.day) return +1;
return 0;
}
}
另外,compareTo() 方法实现的应该是全序关系(total order),满足:
- 非对称性(antisymmerty):若 v \(\leqslant\) w 且 w \(\leqslant\) v,那么 v = w。
- 传递性(transitivity):若 v \(\leqslant\) w 且 w \(\leqslant\) x,那么 v \(\leqslant\) x。
- 完全性(totality):要么 v \(\leqslant\) w 要么 w \(\leqslant\) v 要么 v = w。
石头剪刀布就不符合传递性,课程还举了个反例:double 的 \(\leqslant\):
violates totality: (Double.NaN <= Double.NaN) is false
最后,课程说把对要排序的数组的操作封装成下面两个方法:
// Is item v less than w?
private static boolean less(Comparable v, Compareble w) {
return v.compareTo(w) < 0;
}
// Swap item in array a[] at index i with the one at index j
private static void exch(Compareble[] a, int i, int j) {
Comparable swap = a[i];
a[i] = a[j];
a[j] = swap;
}
交换和比较大小是很常用的操作,而且可以保证能像下面这样检查数组是否有序:
private static boolean isSorted(Comparable[] a) {
for (int i = 1; i < a.length; i++)
if (less(a[i], a[i - 1])) return false;
return true;
}
因为你只对数组元素进行交换和比大小操作,只有最后有序了才能通过上面的测试。要是还允许其它操作,比如全部赋值成 1,那也可以通过上面的测试,但显然不算完成排序。总之大概就是封装抽象出这两操作,会比较方便,不管是排序还是测试。而且便于理解,也增强了代码可移植性,将 less() 改成 v < w 就可以支持没实现 Comparable 接口的基本数据类型。
selection sort
选择排序的思想很简单,第一次选整个数组最小的放在第一位,然后再从第二个位置开始选最小的放在第二位,一直到最后,数组也就排好序了。
例图:
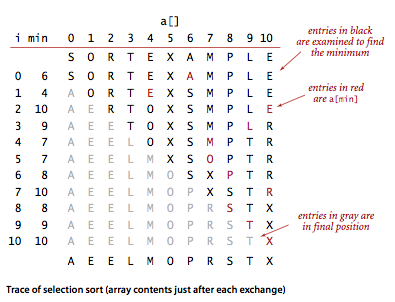
第一次选择 a[0] ~ a[10] 中最小的 A,和第一个位置交换;第二次选 a[1] ~ a[10] 中最小的 E,和第二个位置交换;第三次选 a[2] ~ a[10] 中最小的 E,和第三个位置交换 ... 。
代码:
public class Selection {
public static void sort(Comparable[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
int min = i;
for (int j = i + 1; j < N; j++)
if (less(a[j], a[min]))
min = j;
exch(a, i, min);
}
}
private static boolean less(Comparable v, Comparable w) {...}
private static void exch(Comparable[] a, int i, int j) {...}
}
选择排序对一个大小为 N 的数组排序,需要 (N - 1) + (N - 2) + ... + 1 + 0 ~ \(N^{2}/2\) 次比较和 N 次交换,不管输入的数组是否有序,都需要这么多次的比较,但它交换的次数是最少的,每个元素交换一次就到了最终的位置。
insertion sort
插入排序和选择排序一样,要从左到右遍历数组,过程中左边部分都是有序的,每次把新元素插入到左边合适的位置,例图:
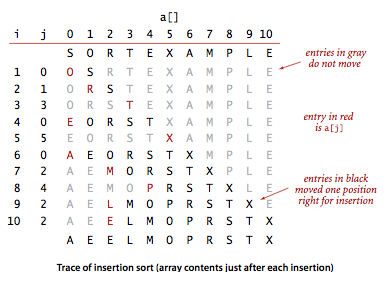
前三次新元素比较大,直接插入到左部末尾,第四次把 E 插入到左边起始位置,第五次 X 也是直接插入到末尾,可以感受到插入排序的比较和交换次数和具体输入有关,不像选择排序是输入无关的。
代码:
public class Insertion {
public static void sort(Comparable[] a) {
int N = a.length;
for (int i = 0; i < N; i++)
for (int j = i; j > 0; j--)
if (less(a[j], a[j - 1]))
exch(a, j, j - 1);
else break;
}
private static boolean less(Comparable v, Comparable w) {...}
private static void exch(Comparable[] a, int i, int j) {...}
}
最好情况下,输入数据本来就是有序的,插入排序都不用交换,只要 N - 1 次比较,时间复杂度为 O(N);最坏情况,输入数据是逆序的,比较和交换都要 1 + 2 + ... + (N - 1) ~ \(N^{2}/2\) 次,时间复杂度为 O(\(N^{2}\));对于随机排列的数据,平均情况下插入排序需要 ~\(N^{2}/4\) 次比较和 ~\(N^{2}/4\) 次交换(详细证明不清楚,问题不大)。
虽然插入排序最坏情况下也是 O(\(N^{2}\)) 级别,但是能够马上发现有序数组每个元素就在合适位置上,插入排序对部分有序的(partially-sorted)数组也很有效。如果数组里逆序对(inversion)的数量小于数组大小的常数倍,就说这数组是部分有序的。逆序对即数组里不符合排序要求的元素对,有序的话就没有,例子:

插入排序每次交换都会减少一个逆序对,所以需要的交换次数即等于逆序对数目。而比较的次数最多等于交换次数加上 N - 1,有可能比较了不交换,所以会多。总的来看,部分有序数组的逆序对小于数组大小的某个常数倍,而插入排序需要的比较和交换次数小于逆序对的某个常数倍,所以插入排序能在线性时间内排好部分有序的数组。对小规模的部分有序数组,插入排序很可能是最快的。
shellsort
希尔排序是插入排序的改进,插入排序每次交换只能把元素移动一位,要是数组很大,又要把元素插入到很远的地方,就会有很多次的比较和交换。希尔排序基于这缺点,一开始先在间隔 h 的元素里比较交换,交换成功相当于直接移动了 h 位,也减少了逆序对,数组更加有序;再用更小的步长 g 同样比较交换,因为 g < h,而且逆序对肯定不会变多,这步的交换后,数据还是 h 有序的;最后步长为 1 就是插入排序了,不过有前面的几次排序,逆序对少的数组排起来就很快了。
例图:

现在有个很重要的问题是每次排序的步长怎么选择,Knuth 提出序列 3X + 1(1, 4, 13, 40,...),可以证明最坏情况下需要的比较次数和 \(N^{3/2}\) 成正比,也很容易计算。
代码:
public class Shell {
public static void sort(Comparable[] a) {
int N = a.length;
int h = 1;
while (h < N/3) h = h*3 + 1; // 1, 4, 13, 40,...
while (h >= 1) {
// h-sort the array
for (int i = h; i < N; i++) {
for (int j = i; j >= h && less(a[j], a[j - h]); j -= h)
exch(a, j, j - h);
}
h = h/3;
}
}
private static boolean less(Comparable v, Comparable w) {...}
private static void exch(Comparable[] a, int i, int j) {...}
}
希尔排序的性能分析至今还是一个开放问题,没有准确的模型可以描述,在数学上还不知道对于随机数据需要的平均比较次数,还有最优步长序列又是什么。但是,这些问题偏学术性,实际使用中,对于中等规模的数组,希尔排序是一个很不错的选择,运行时间可以接受(复杂算法可能只会快两倍),代码简单,也不需要额外的空间。
shuffling
洗牌(shuffle),大概算排序的一种应用?给牌随机一个区间 (0, 1) 上的值,然后用排序来洗牌。不过,感觉介绍的另一个 Knuth Shuffling (Fisher–Yates shuffle 1938) 算法更值得一看。
代码:
public class StdRandom {
...
public static void shuffle(Object[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
int r = StdRandom.uniform(i + 1); // between 0 and i
exch(a, i, r);
}
}
}
遍历一遍就好,可以在线性时间内得到随机序列,循环到 i 时将其和区间 [0, i] (或 [i, N - 1])上的随机位置交换。至于算法的正确性,考虑跑完之后序列不变的概率:第一次循环,第一张牌在位置 1 的概率为 1/1;第二次循环,第二张牌在位置 2 的概率为 1/2;... 所有牌都在原来位置的概率为 1/1 * 1/2 * ... * 1/N = 1/N!,而每个循环放其它位置的概率一样,同理得到其它序列的概率也是 1/N!,所以满足随机性。这样解释好像挺通的,或者看找到的一个更复杂的证明:試證明 Knuth Shuffle 為均勻的。
小小的拓展是从 N 个元素里随机挑选 m 个,其中 m < N,第二次编程作业里也有涉及到。一开始直接放前 m 个,i 从 m + 1 到 N 时每次在区间 [0, i] 上随机得到 k,若 k < m,则把位置 k 的数换成 i 的,大于不管,也只要遍历一次。
代码:
public static int[] randomSample(int[] nums, int m) {
if (nums == null || nums.length == 0 || m <= 0) {
return new int[]{};
}
int[] sample = new int[m];
for (int i = 0; i < m; i++) {
sample[i] = nums[i];
}
Random random = new Random();
for (int i = m; i < nums.length; i++) {
int k = random.nextInt(i + 1); // 0~i(inclusive)
if (k < m) {
sample[k] = nums[i];
}
}
return sample;
}
代码来自 Shuffle and Sampling - 随机抽样和洗牌,也有上面两个算法正确性的讨论,或者后面的证明可以看原来编程作业找到的大狸子先生。
convex hull
介绍了用到排序的凸包(convex hull)问题,已知一些点,问题即是找到把它们包起来的多边形的点,如下图:
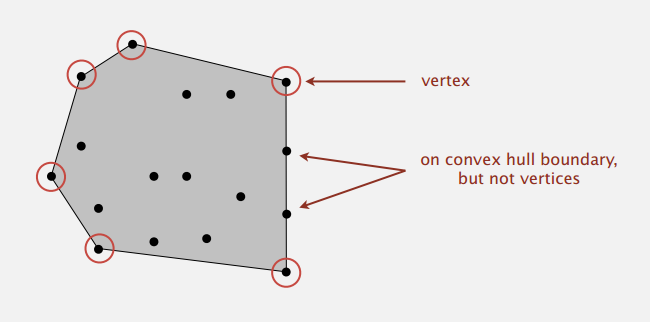
应用场景比如有机器人找绕过障碍物的最短路径(下左),找这些点间最大的距离(下右)。
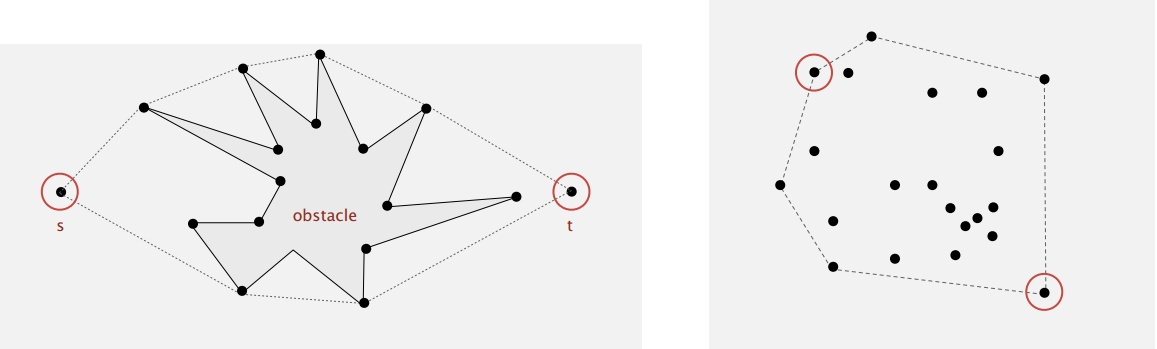
凸包有两个几何特性(geometric properties):
-
可以按逆时针方向遍历目标点。
-
目标点按和 y 坐标最小的点的极角升序排列。
Graham 扫描算法基于上面两个事实来找到目标点。
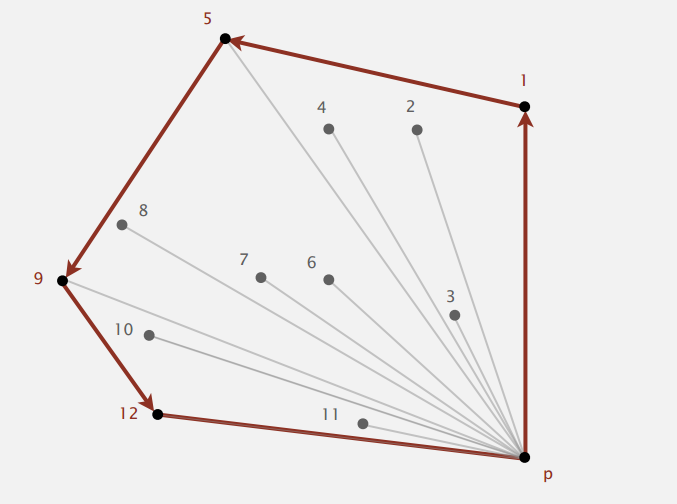
P 点的 y 坐标最小,其它点按与 P 的极角排序,上图已经编好号,按顺序一个个处理。点 1 先放进去,再把点 2 放进去,现在三个点 1,2,P 符合逆时针方向,继续下一个点;放点 3,点 1,2,3 符合逆时针方向;再放点 4,这时点 2,3,4 不符合逆时针方向,回退 丢掉点 3,点 1,2,4 还是不符合逆时针方向,继续回退丢掉点 2,点1,4,P 符合逆时针方向,然后再继续下一个点;... 结合上图,显然最后会得到的目标点。
具体的实现,排序部分会在接下的课程里体现,以后再说;判断是否符合逆时针方向部分,花了不少时间理解下面那页 PPT,顺便回炉重造了下线性代数。另外 B 站是个学习的好地方: 线性代数的本质,也有 算法第四版,Coursera 经常放不了。
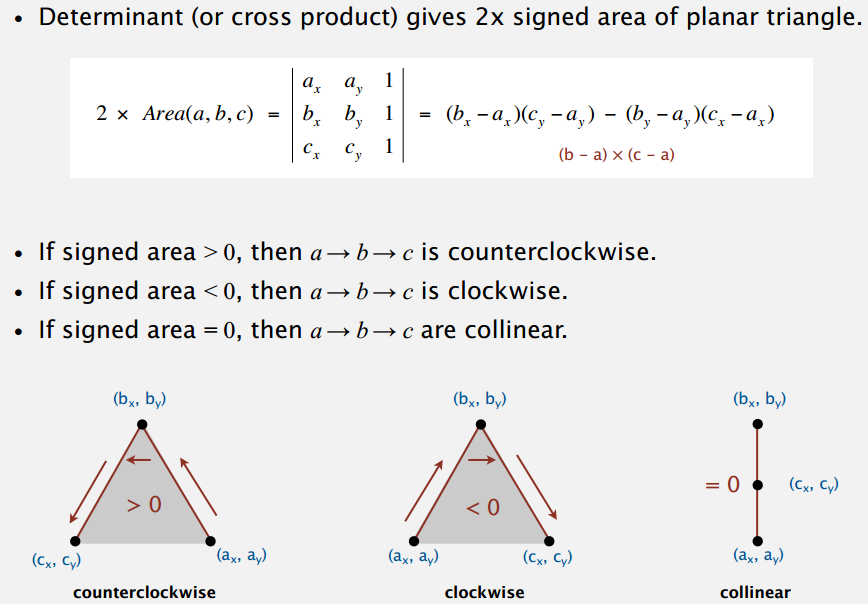
知道三个点的坐标,判断是否是逆时针方向,借助算围成的三角形的面积来做。上面等式的头尾是两个向量叉乘的几何意义:大小等于以它们为边的平行四边形的面积,三角形自然就是一半。不过叉乘好像是定义在三维空间上的,这边应该是把 Z 坐标默认为 0 来算二维?但也有看到二维向量叉乘直接等于二阶行列式的,个人觉得直接用二阶行列式解释面积更合适,还是叉乘的右手定则比较好让人判断方向。好像不是很严格也没关系,随便啦。
In computational geometry of the plane, the cross product is used to determine the sign of the acute angle defined by three points \(p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})\) and \(p_{3}=(x_{3},y_{3})\). It corresponds to the direction (upward or downward) of the cross product of the two coplanar vectors defined by the two pairs of points \((p_{1},p_{2})\) and \((p_{1},p_{3})\). The sign of the acute angle is the sign of the expression
\(P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})\),
which is the signed length of the cross product of the two vectors.
摘自 wiki。
至于中间的那个三阶行列式,总觉得不该只是计算上的巧合。我觉得,根据行列式的几何意义,中间那个等于以向量 (\(a_{x}\), \(a_{y}\), 1),(\(b_{x}\), \(b_{y}\), 1),(\(c_{x}\), \(c_{y}\), 1) 为边的平行六面体的体积,然后以这三向量为棱边的三棱锥的体积是前面那个平行六面体的六分之一(想象一下特例正方体),同时三棱锥体积还可以用三个点围的三角形和 z 轴上的高 1 乘三分之一来算,于是可以算出三角形面积等于二分之一的三阶行列式。好像可以这样想,感觉解释得通。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号