求数组中未出现的最小正整数（408-18/力扣41）

方法一：

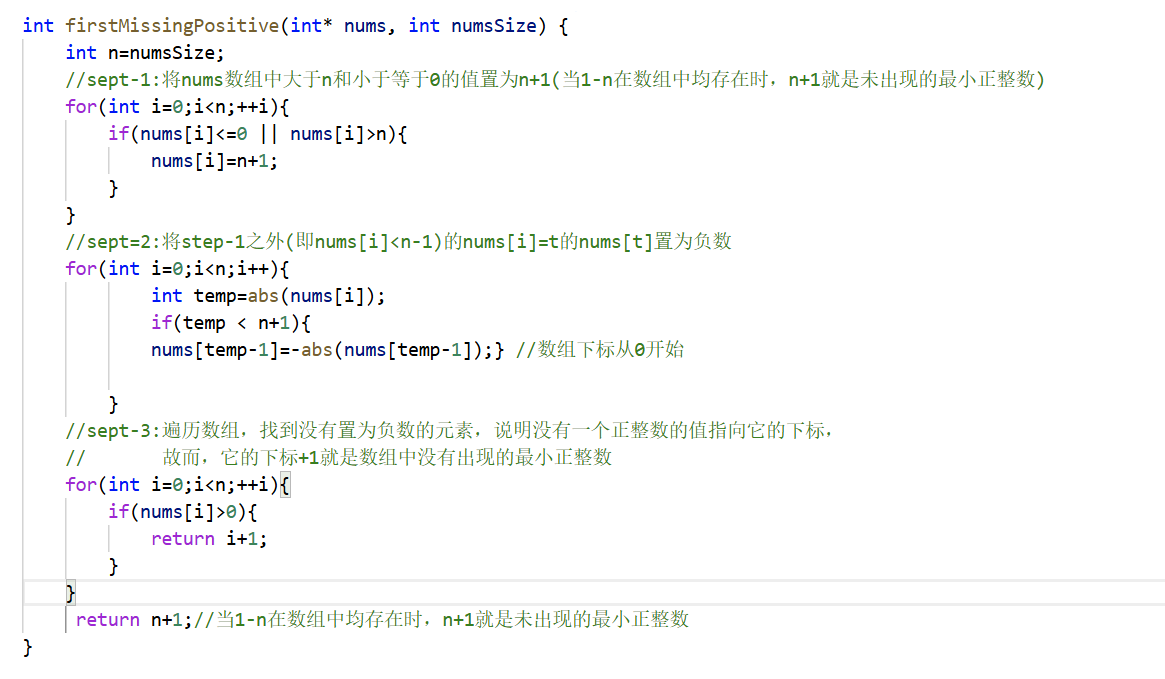
解释： 将小于0和大于数组长度（n/numsSize）的元素的值均置为n+1,当数组是{1,2,3,4,5···}时，n+1就是未出现的最小正整数；
将大于0且小于n的元素的值-1指向的数组下标的值置为负数，遍历数组中符合前提条件的所有值，举例说明数组{1，2,4，5}，
其中1-1=0,则将数组下标为0的元素值置为负数，也就是1-->-1，同理，2-->-2,4-->-5,5大于numsSize,不管。于是数组
变为{-1，-2, 4, 5 }，最后，遍历数组，找到第一个元素值为正的元素，它的下标+1就是未出现的最小正整数。
PS：当数组为{1,2，3,4}时的到{-1，-2，-3，-4}这种情况n+1就是未出现的最小正整数。
时间复杂度：O(3n)=O(n); 空间复杂度：O(1)

方法二：

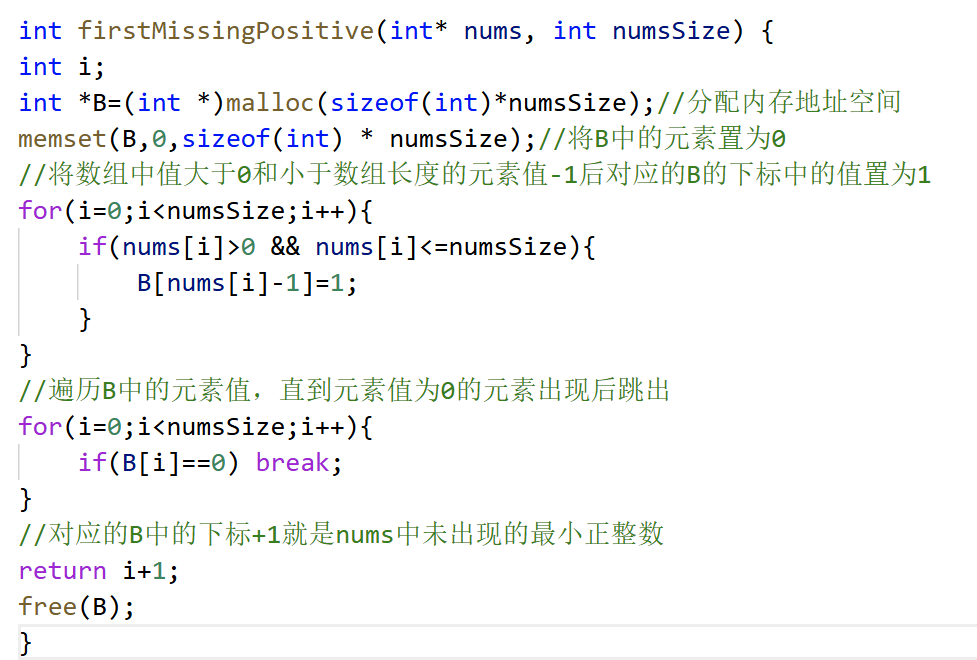
解释：创建一个长度和nunms相等的数组B并将其中的值全置为0，接着对于nums中大于0且小于n的元素的值-1对应B中下标，
将对应的下标中的元素值置为1，如数组{1,3,2,5}，将得到B{0,0,0,0}--->{1,1,1,0}
最后遍历数组B中的元素，找到第一个值为0的元素，对应的下标值就是未出现的最小正整数。

时间复杂度：O(3n)=O(n); 空间复杂度：O(n)
PS：对于B的置0的时间复杂度为O(n)

有趣的事：
对于方法一中的第二步，有一个奇怪的错误

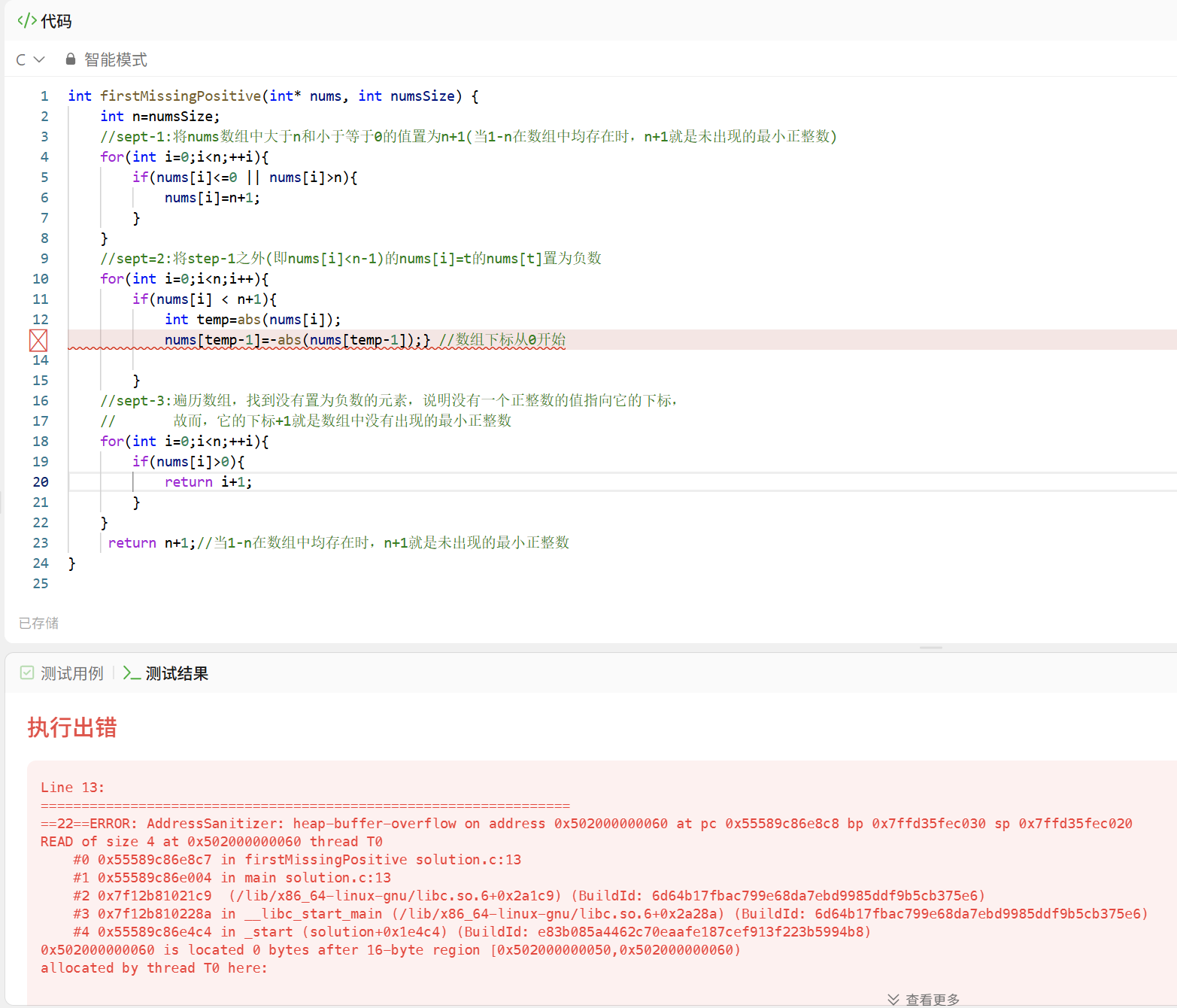
这是力扣中可以执行的方法

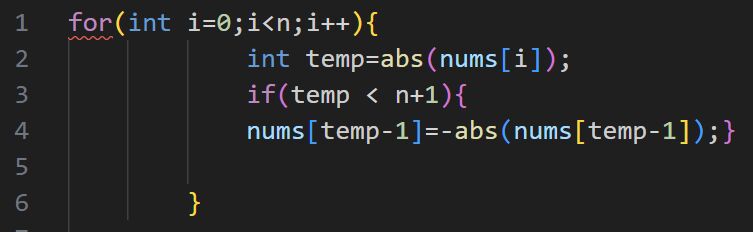
这是在力扣中会报错（但是在vscode中能执行）的方法

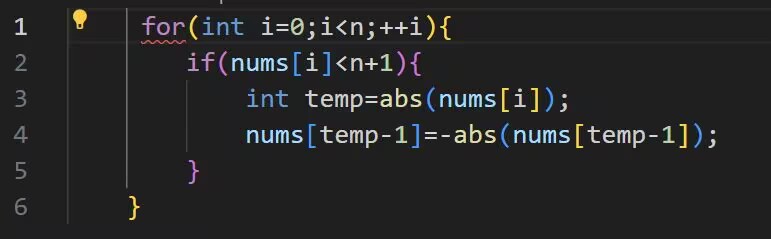
原因是什么，我暂时没有答案，逻辑上我认为两种都行，猜测原因跟线程有关，
但是那部分内容不是我近期学习的主要内容，其次报错的说明是数组下标越界，
有空再说，有同学解答那自然是更好，感谢！