第十三讲-变号级数收敛性判别方法
本讲考虑对非正项的级数怎么判定?先介绍了变号级数的特殊的交错级数的概念,并用莱布尼兹法进行判定(级数的通项 单调减少;级数的通项极限为0);又考虑一般情况下的变号级数,去绝对值构造的正项级数和原级数有密切关系,并引出条件收敛和绝对收敛的概念,并回答了一开始的问题:绝对收敛的级数满足交换律。
然后介绍了两个绝对收敛的级数的相乘的规律(柯西乘积),最后介绍一般级数的判定方法。
问题导入

交错级数
所谓交错级数, 就是正负项交错的级数. 更准确地, 设 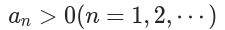
, 称级数
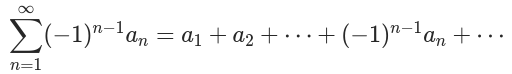
为交错级数.
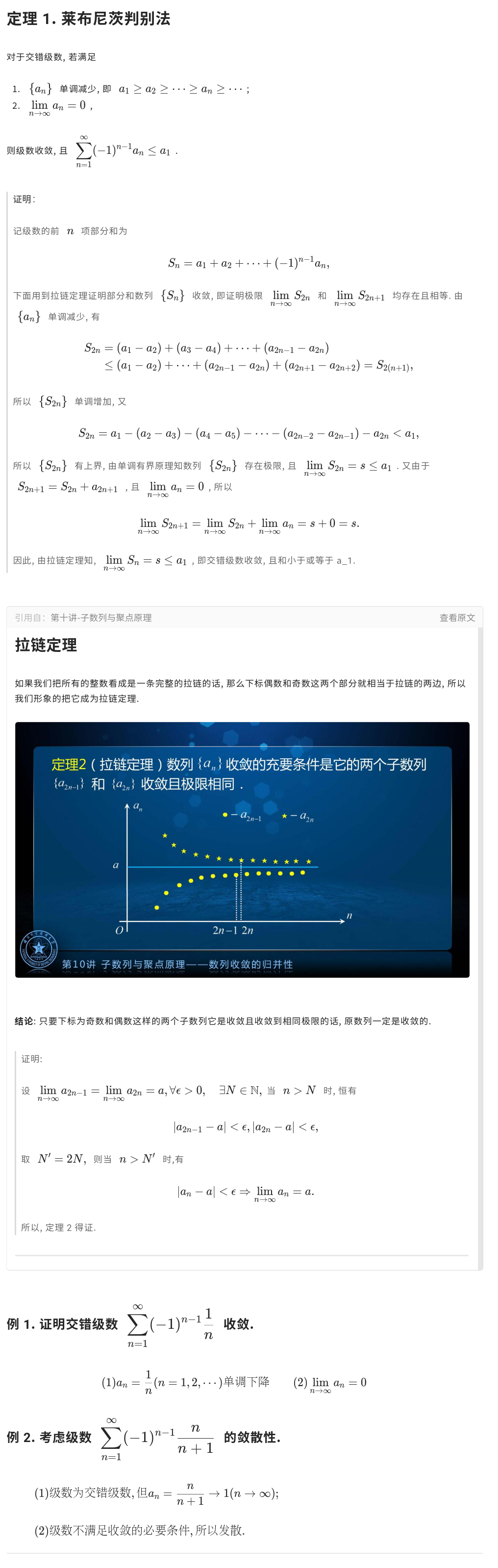
变号级数
并不是所有变号级数都呈现交错级数的形式, 即使是交错级数也不一定满足单调性的条件, 因此我们需要探求判断其他变号级数敛散性的方法.

级数收敛性判定一般方法
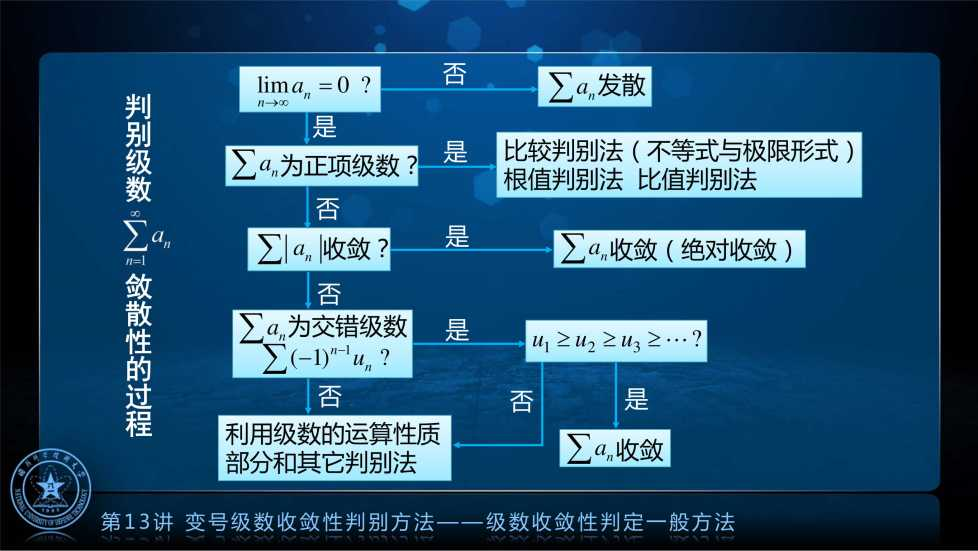
一般方法的应用
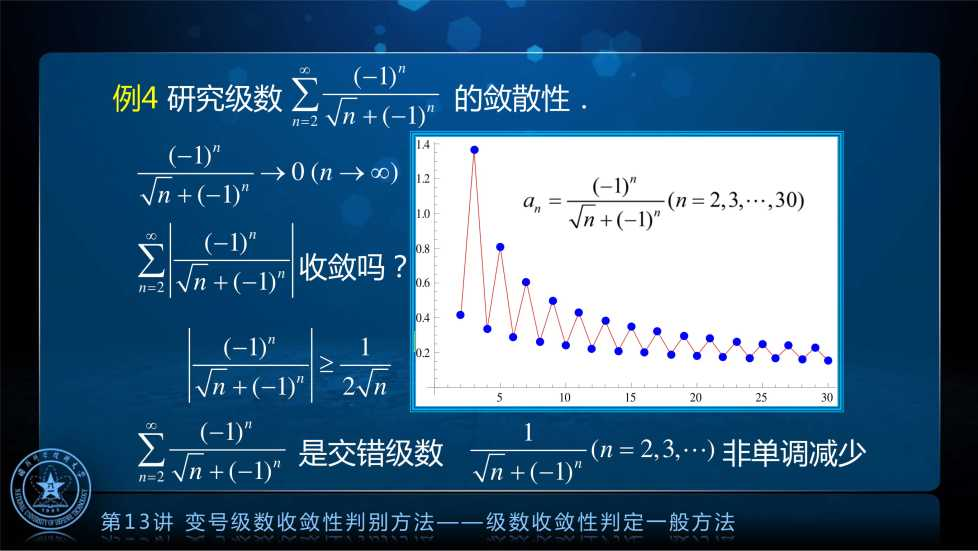
研究级数 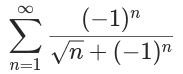 的收敛性.
的收敛性.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号