常见概率分布及python实现
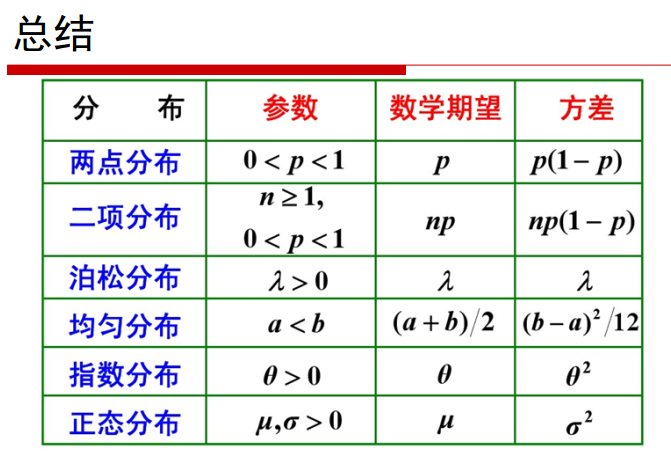
1.两点分布——离散型概率分布
概念:一次试验,若成功随机变量取值为1,成功概率为p; 若失败随机变量取0,失败概率为1-p
期望\(E(X)=1*p+0*(1-p)=p\)
方差
\[\begin{aligned}
D(X)&=p*(1-p)^2+(1-p)*(0-p)^2\\
&=p(1-p)
\end{aligned}
\]
2.二项分布——离散型概率分布
概念:进行n次伯努利试验。(n>=1),当n=1,二项分布就是伯努利分布
n次试验中总共成功的次数为k的概率 \(P(X=k;n,p)=C_n^k*p^k*(1-p)^{n-k}\)
期望 $ E(X)=np $
期望的推导
\[\begin{aligned}
E(X) &= \sum_{k=0}^{n}k*P(X=k)\\
&=\sum_{k=0}^{n}k*\frac{n!}{k!(n-k)!}p^k (1-p)^{n-k}\\
&=np\sum_{k=1}^{n}\frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1} (1-p)^{(n-k)}\\
&=np
\end{aligned}
\]
方差$ D(X)=np(1-p) $
方差的推导
\[\begin{aligned}
D(X) &= E(X^2)-E^2(X)\\
&=E[X(X-1)+X]-n^2p^2=E[X(X-1)]+np-n^2p^2
\end{aligned}
\]
\[\begin{aligned}
E[X(X-1)] &= \sum_{k=0}^{n}k(k-1)*P(X=k)\\
&= \sum_{k=0}^{n}k(k-1)*\frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}\\
&=n(n-1)p^2\sum_{k=2}^{n}\frac{(n-2)!}{(k-2)!(n-k)!}p^{k-2}(1-p)^{n-k}\\
&=n(n-1)p^2
\end{aligned}
\]
\[\begin{aligned}
D(X)&=n(n-1)p^2+np-n^2p^2\\
&=np(1-p)
\end{aligned}
\]
3.泊松分布——离散型概率分布
泰勒展开式
\[\begin{aligned}
e^x&=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots+ \frac{x^n}{n!}+R_n\\
1&=e^{-x}+xe^{-x}+\frac{x^2}{2!}e^{-x}+\frac{x^3}{3!}e^{-x}+\cdots+\frac{x^n}{n!}e^{-x}+R_ne^{-n}
\end{aligned}
\]
通项 $ \frac{xk}{k!}e $ ---> \(\frac{\lambda^k}{k!}e^{-\lambda}\)
概率分布\(P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda},\lambda>0,k=0,1,2,\cdots\)
期望
\[\begin{aligned}
E(X)&=\sum_{k=0}^{\infty}k*f(x)\\
&=\sum_{k=0}^{\infty}k*\frac{\lambda^k}{k!}e^{-\lambda}\\
&=\lambda\sum_{k=1}^{\infty}\frac{\lambda^{k-1}}{(k-1)!}e^{-\lambda}\\
&=\lambda
\end{aligned}
\]
方差
\[\begin{aligned}
D(X) &= E(X^2)-E^2(X)\\
&=E[X(X-1)+X]-E^2(X)\\
&=E[X(X-1)]+E(X)-E^2(X)\\
&=E[X(X-1)+\lambda-\lambda^2
\end{aligned}
\]
\[\begin{aligned}
E[X(X-1)&=\sum_{k=0}^{\infty}k(k-1)*\frac{\lambda^k}{k!}e^{-\lambda}\\
&=\lambda^2\sum_{k=2}^{\infty}\frac{\lambda^{k-2}}{(k-2)!}e^{-\lambda}\\
&=\lambda^2
\end{aligned}
\]
\[\begin{aligned}
D(X)&=E[X(X-1)]+E(X)-E^2(X)=\lambda^2+\lambda-\lambda^2=\lambda
\end{aligned}
\]
泊松分布的期望和方差都是参数\(\lambda\)!
import numpy as np
a = np.random.poisson(55,size=(4,))
print(a)
print(type(a))
>>> [46 50 39 57]
<class 'numpy.ndarray'>
4.均匀分布——连续型概率分布
概率密度函数为
\[f(x)=\left\{
\begin{aligned}
&\frac{1}{b-a},&a<x<b\\
&0,&others
\end{aligned}
\right.
\]
期望\(E(X)=\int_{-\infty}^{\infty}x*f(x)dx=\frac{a+b}{2}\)
方差\(D(X)=E(X^2)-E^2(X)=\int_{a}^{b}x^2*\frac{1}{b-a}dx-\frac{(a+b)^2}{4}=\frac{(b-a)^2}{12}\)
#np.random.uniform(low=0.0, high=1.0, size=None)
a = np.random.uniform(20,50,size=(2,6))
print(a)
print(type(a))
>>> [[ 45.20217569 43.75312926 26.52703807 41.91200572 42.85374841
29.24479553]
[ 45.12516381 30.12544796 35.53555014 32.28527649 21.76682194
46.33104556]]
<class 'numpy.ndarray'>
5.指数分布——连续型概率分布
概率密度函数为
\[f(x)=\left\{
\begin{aligned}
&\frac{1}{\theta}e^{-\frac{x}{\theta}},&x>0,\\
&0,&x\leq0
\end{aligned}
\right.
\]
其中\(\theta>0\)
期望
\[\begin{aligned}
E(X)&=\int_0^{+\infty}x*f(x)dx\\
&=\int_0^{\infty}x\frac{1}{\theta}e^{-\frac{x}{\theta}}dx\\
&=-\int_0^{\infty}xd(e^{-\frac{x}{\theta}})\\
&=-[xe^{-\frac{x}{\theta}}|_0^{\infty}-\int_0^{\infty}e^{-\frac{x}{\theta}}dx]\\
&=\theta
\end{aligned}
\]
方差
\[\begin{aligned}
D(X)&=E(X^2)-E^2(X)\\
&=\int_0^{+\infty}x^2\frac{1}{\theta}e^{-\frac{x}{\theta}}-\theta^2\\
&=2\theta^2-\theta^2\\
&=\theta^2
\end{aligned}
\]
6.正态分布/高斯分布
设随机变量X服从正态分布,即X~\(N(\mu,\sigma^2)\)
概率密度函数为
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\]
期望\(E(X)=\mu\)
方差\(D(X)=\sigma^2\)
a = np.random.normal(40,3,size=(5,2))
print(a)
print(type(a))
>>>[[ 42.75053239 36.92362467]
[ 42.90588338 38.58249427]
[ 42.91278062 39.05507689]
[ 39.69794259 40.26237062]
[ 38.90643225 42.94278753]]
<class 'numpy.ndarray'>


 浙公网安备 33010602011771号
浙公网安备 33010602011771号