详解Kalman Filter

中心思想

现有：

1. 已知上一刻状态，预测下一刻状态的方法，能得到一个“预测值”。（当然这个估计值是有误差的）
2. 某种测量方法，可以测量出系统状态的“测量值”。（当然这个测量值也是有误差的）

我们如何去估计出系统此时真实的状态呢？
答案是需要结合“预测值”和“测量值”。例如我们可以加权求和，但是这个权重要怎么定义，才能准确估计出真实状态呢？这个权重就是Kalman Filter解决的事情。

系统建模

预测方法

\[x_k=F_kx_{k-1}+B_ku_k+w_k \]

我们假设这个预测方法是线性变换，\(B_ku_k\)是除了状态转移之外的控制量。\(w_k\)是预测误差，假设为高斯分布（即均值为0的多元正态分布），其协方差矩阵为\(Q_k\)。
也就是说，下一刻我们的预测值，有一部分与上一刻状态有关，一部分与外力控制有关（外力控制与上一刻状态无关），还有一部分被噪声所影响。
举个例子：
假设一小车在x轴上向前以速度\(v\)匀速运动，\(x_k\)表示的是k时刻小车在x轴上的坐标。显然我们有$$x_k=x_{k-1}+vt$$，这里速度v和时间t都和上一个状态无关，属于让小车位置变化的“外力”。在这个例子里\(F_kx_{k-1}\)部分就是\(x_{k-1}\)，而\(B_ku_k\)部分就是\(vt\)。

测量方法

\[z_k=H_kx_k+v_k \]

因为我们不一定有测量仪器能直接测量出系统状态，因此我们假设测量方法也是线性变换。
也就是说，当我们的测量仪器用于测量系统状态\(x_k\)时，它的读数是系统状态加上一定的线性变换\(H_k\)，以及测量噪声\(v_k\)，假设为高斯分布（即均值为0的多元正态分布），其协方差矩阵为\(R_k\)。
举个例子：
我们称体重需要得到以“斤”为单位的数据，这是系统状态，但是我们的称只能读出单位为“kg”的数据（这就是\(z_k\)），那我们就需要做一个单位转换（对应\(H_k\)），此外，由于称不一定准，所以最后称的读数还得加上一点噪声。

所有参数中：\(F_k\)、\(B_k\)、\(u_k\)、\(Q_k\)、\(H_k\)、\(R_k\)都需要已知，要么自己根据公式和经验定义，要么从样本数据里估计一个值。

算法

Kalman Filter将一直维护对系统状态\(x_k\)的最优估计值，以及这个估计值的偏差：

• \(\hat{x}_k\)，系统状态，可以是多维的。
• \(P_k\)，\(\hat{x}_k\)的误差。当\(\hat{x_k}\)是一维时，\(P_k\)是方差；当\(\hat{x_k}\)是多维时，\(P_k\)是协方差\(cov(\hat{x_k})\)，就是\(\hat{x_k}\)里各维两两协方差。

预测阶段

首先，通过系统的预测方法，我们可以得到“预测值”：

\[\bar{x_k}=F_k\hat{x}_{k-1}+B_ku_k \]

由于误差不知道，且假设其均值为0，所以这里不算误差
那么协方差也可以从上一个状态转移：

\[\bar{P}_k=F_kP_{k-1}F_k^T+Q_k \]

更新阶段

这个阶段需要结合“预测值”和“测量值”。先把具体的方程摆上来：

• 计算测量值残差（innovation/measurement pre-fit residual）：\(\tilde{y}_k=z_k-H_k\bar{x_k}\)（我的理解是\(H_k\)就是为了把测量值和预测值转换到同一个空间）
• 计算测量值残差的协方差（Innovation (or pre-fit residual) covariance）：\(S_k=H_k\bar{P}_kH_k^T+R_k\)
• 计算卡尔曼增益（Kalman Gain）：\(K_k=\bar{P}_kH_k^TS_k^{-1}\)
• “更新” 最终得到的估计值：\(\hat{x}_k=\hat{x}_{k-1}+K_k\tilde{y}_k\)
• “更新” 最终得到的估计值的协方差：\(P_k=(I-K_kH_k)P_{k-1}\)

总之最后的算法就是，每得到一个“测量值”，就重复一遍预测和更新阶段。

\(\mathbf{K}\)就是Kalman Gain，它衡量了“测量值”和“预测值”之间的权重比例，\(\mathbf{K}\)越大，“测量值”所占权重越大。从公式可以看出:

• \(Q_k\)越大，\(\bar{P}_k\)越大，\(\mathbf{K_k}\)越大。这从物理意义上也是说得通的，当预测值的误差更大的时候，当然应该多信任测量值。
• \(R_k\)越大，\(S_k\)越大，\(\mathbf{K_k}\)越小。也就是说，当“测量值”的误差越大时，该公式将更信任“预测值”。

所有参数中，\(F_k\)、\(B_k\)、\(u_k\)、\(H_k\)基本都需要根据你的问题的建模来决定，而除此之外的\(Q_k\)和\(R_k\)就是两个用于控制预测灵活性的参数，有点类似于指数滑动平均算法的那个\(\alpha\)。

更新阶段原理（试图）详解

结合“预测值”和“测量值”的思想

参考：如何通俗并尽可能详细地解释卡尔曼滤波？ - 肖畅的回答 - 知乎

（结合高斯分布解释）具体公式怎么推导

参考：图说卡尔曼滤波，一份通俗易懂的教程

让我们从一维看起，设方差为\(\sigma^2\)，均值为\(\mu\)，一个标准一维高斯钟形曲线方程如下所示：

\[\mathcal{N}(x,\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

那么两条高斯曲线相乘呢？

\[\mathcal{N}(x,\mu_0,\sigma_0)\cdot\mathcal{N}(x,\mu_1,\sigma_1)=\mathcal{N}(x,\mu',\sigma') \]

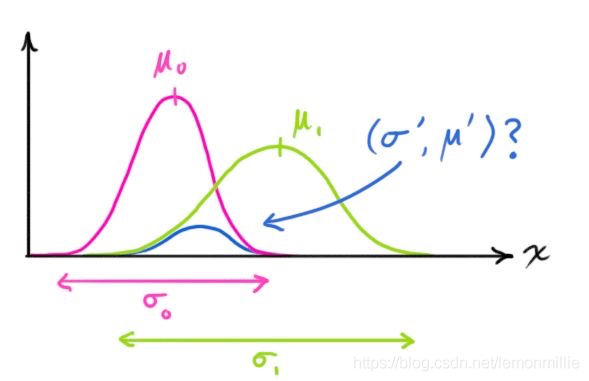
把这个式子按照一维方程进行扩展，可得：

\[\mu'=\mu_0+\frac{\sigma_0^2(\mu_1-\mu_0)}{\sigma_0^2+\sigma_1^2} \]

\[\sigma'^2=\sigma_0^2-\frac{\sigma_0^4}{\sigma_0^2+\sigma_1^2} \]

如果有些太复杂，我们用k简化一下：

\[\mathbf{k}=\frac{\sigma_0^2}{\sigma_0^2+\sigma_1^2} \]

\[\mu'=\mu_0+\mathbf{k}(\mu_1-\mu_0) \]

\[\sigma'^2=\sigma_0^2-\mathbf{k}\sigma_0^2 \]

以上是一维的内容，如果是多维空间，把这个式子转成矩阵格式：

\[\mathbf{K}=\Sigma_0(\Sigma_0+\Sigma_1)^{-1} \]

\[\mu'=\mu_0+\mathbf{K}(\mu_1-\mu_0) \]

\[\Sigma'=\Sigma_0-\mathbf{K}\Sigma_0 \]

其中，\(\Sigma\)表示协方差。
代入到Kalman Filter里，我们把“预测分布”\((\mu_0, \Sigma_0)=(H_k\bar{x}_k,H_k\bar{P}_kH_k^T)\)，和“测量分布”\((\mu_1, \Sigma_1)=(z_k,R_k)\)代入到上面的等式里，那么新分布\((\mu',\Sigma')=(H_k\hat{x}_k, H_kP_kH_k^T)\)为：

这里\((\mu_0, \Sigma_0)=(H_k\bar{x}_k,H_k\bar{P}_kH_k^T)\)乘以了系数\(H_k\)是为了把\(x_k\)转换到和\(z_k\)一个坐标系。

\[K=H_k\bar{P}_kH_k^T(H_k\bar{P}_kH_k^T+R_k)^{-1} \]

\[H_k\hat{x}_k=H_k\bar{x}_k+K(z_k-H_k\bar{x}_k) \]

\[H_kP_kH_k^T=H_k\bar{P}_kH_k^T-KH_k\bar{P}_kH_k^T \]

等式两边消掉\(H_k\)并化简后：

\[K_k=\bar{P}_kH_k^T(H_k\bar{P}_kH_k^T+R_k)^{-1} \]

\[\hat{x}_k=\bar{x}_k+K_k(z_k-H_k\bar{x}_k) \]

\[P_k=(I-K_kH_k)\bar{P}_k \]