Data structure and algorithm-One

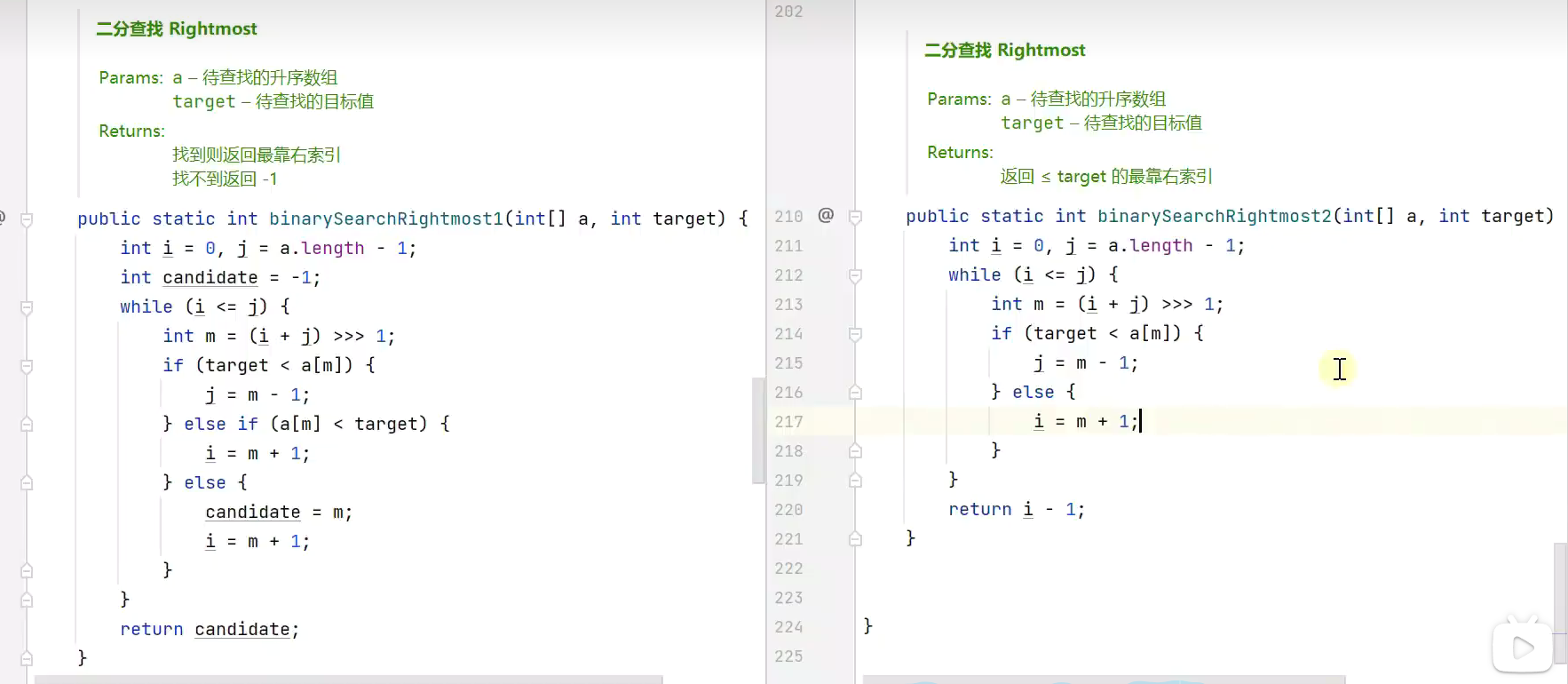
右边界

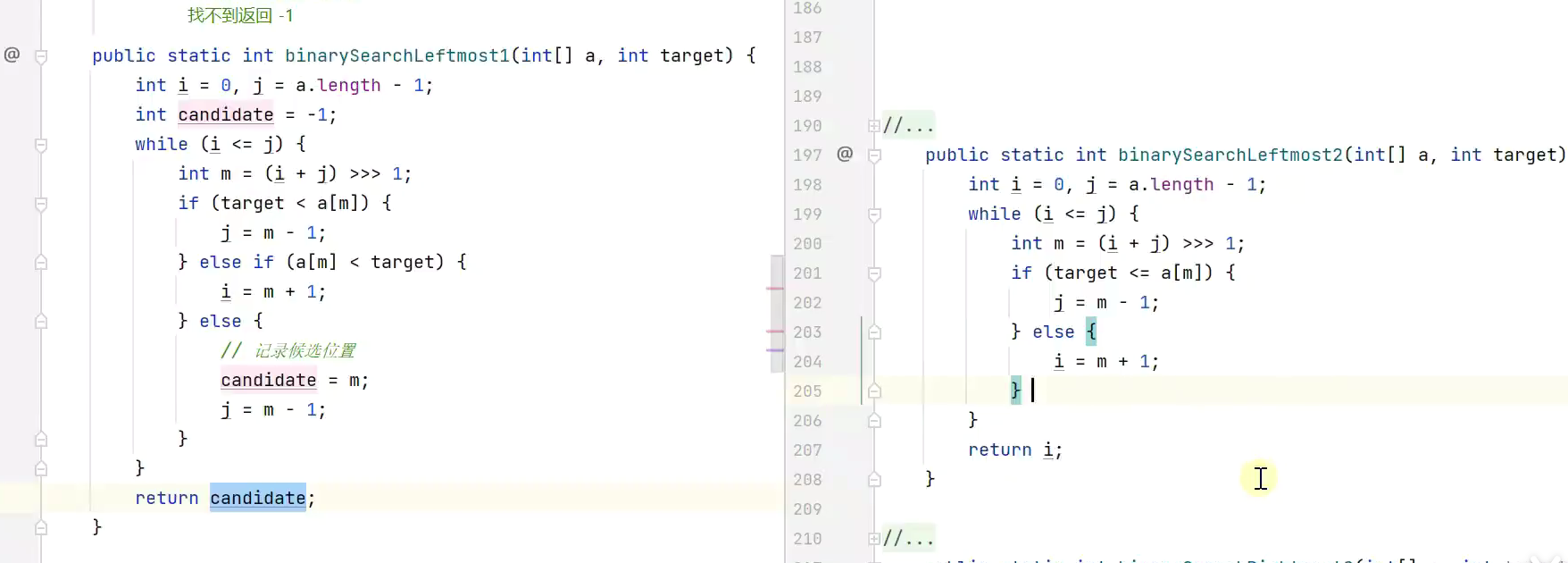
左边界
函数式编程

传统的实现方式通常是将具体的功能代码直接写在方法内部。这样的实现方式对于固定的功能来说可能是足够的，但它的灵活性和复用性较低。每当需要不同的功能时，您需要编写新的方法或修改原有方法，这可能会导致代码的冗余和不易维护。

而函数式编程的优点在于它将函数本身作为参数传递，使得调用者可以根据自己的需要来自定义具体的逻辑实现。通过传递不同的函数（Lambda表达式），可以实现不同的行为，而不需要修改原有的方法。这种特性使得函数式编程更加灵活和可复用。

您的乐高积木的比喻非常合理：传统的实现方式就像是提供了已经拼装好的乐高积木模型，用户只能使用现成的模型，无法进行自由创作。而函数式编程则像是提供了各种零件，用户可以根据自己的创意，自由拼装出不同的模型。

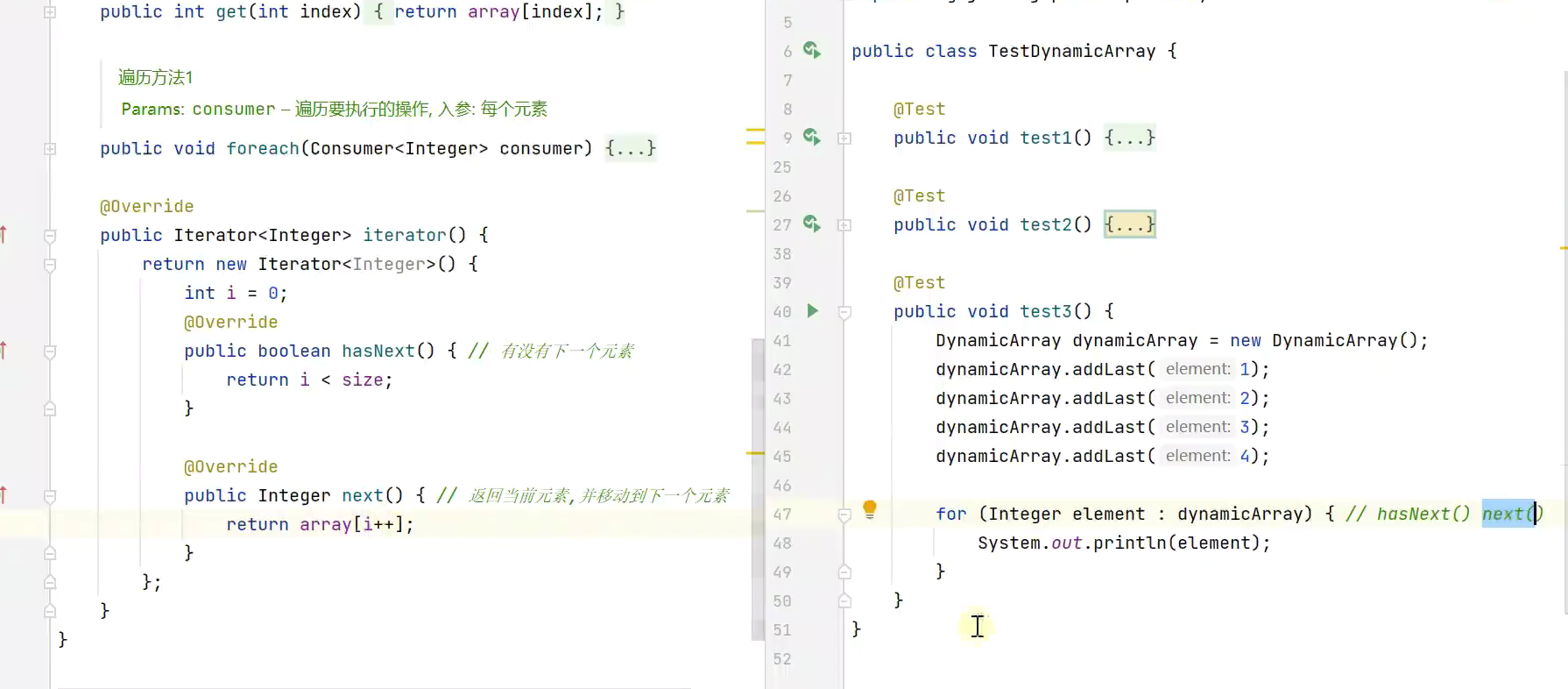
重写迭代器方法

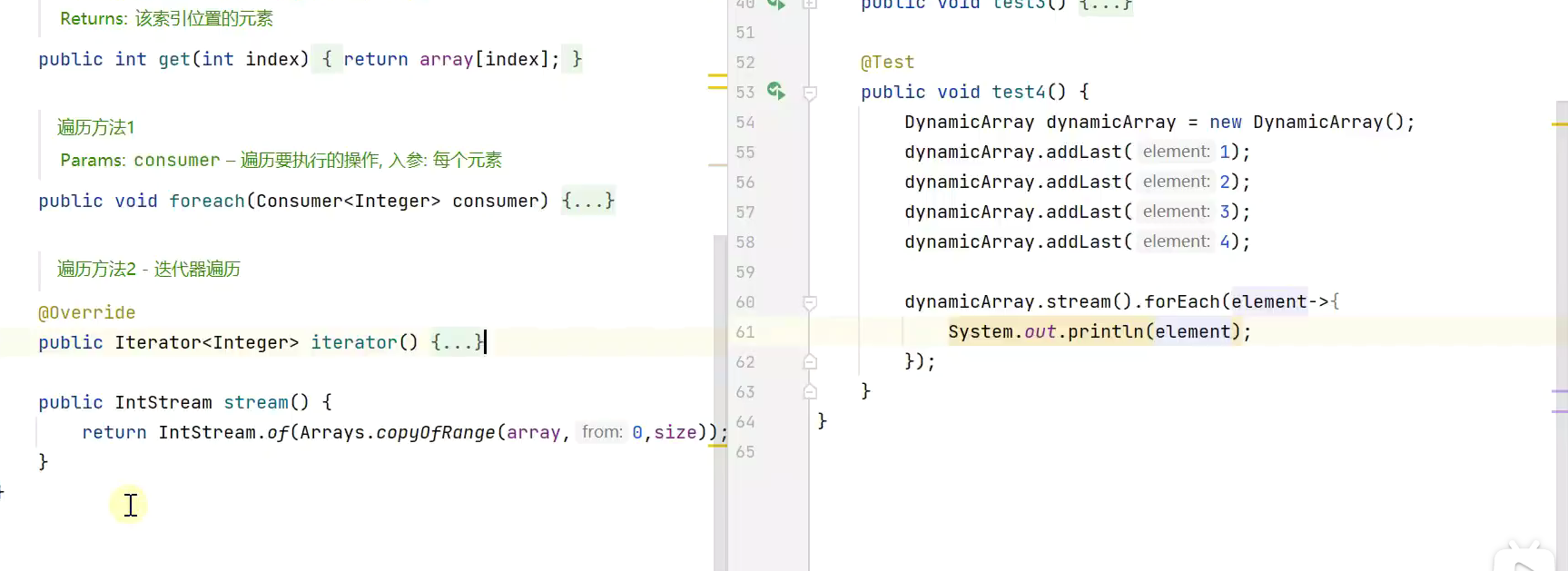
流遍历
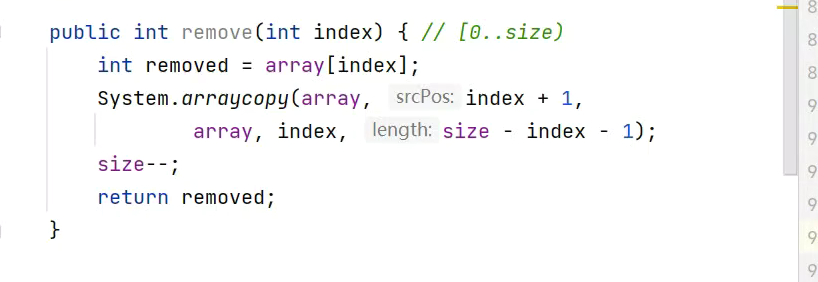
数组删除

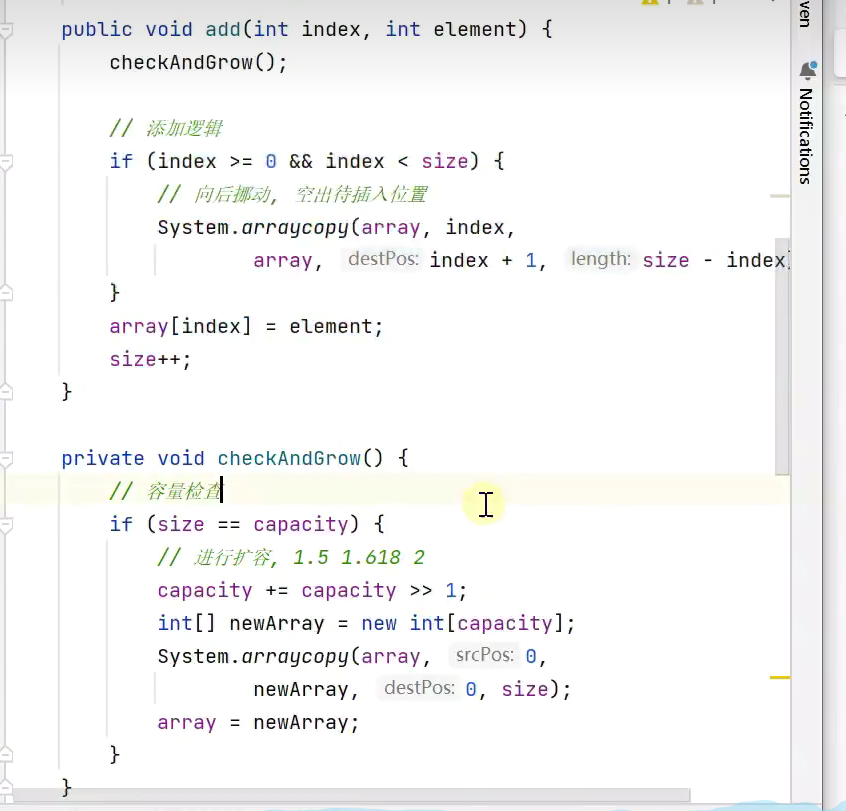
添加并检查是否需要扩容

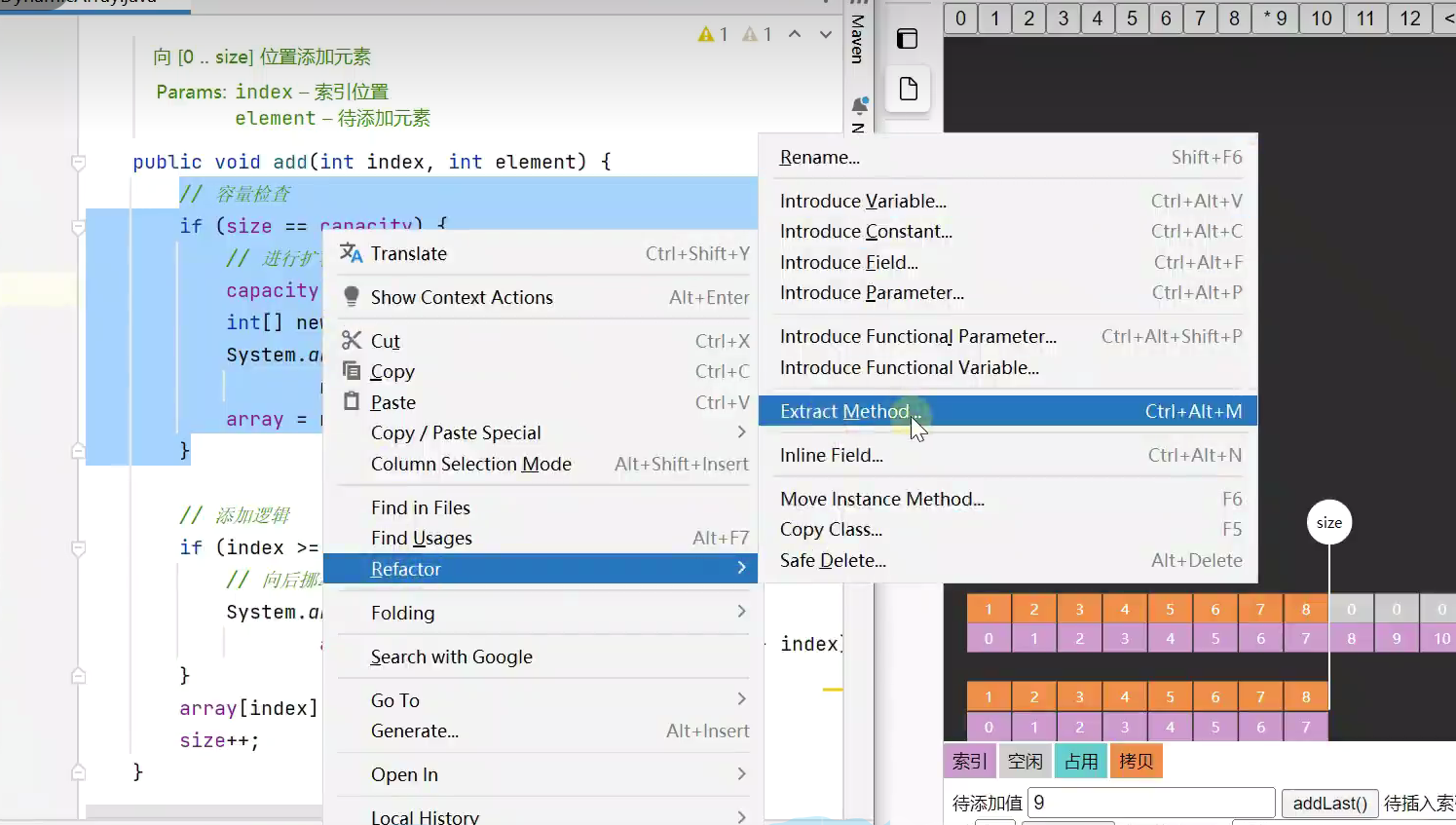
抽取方法
CTRL + Alt + m
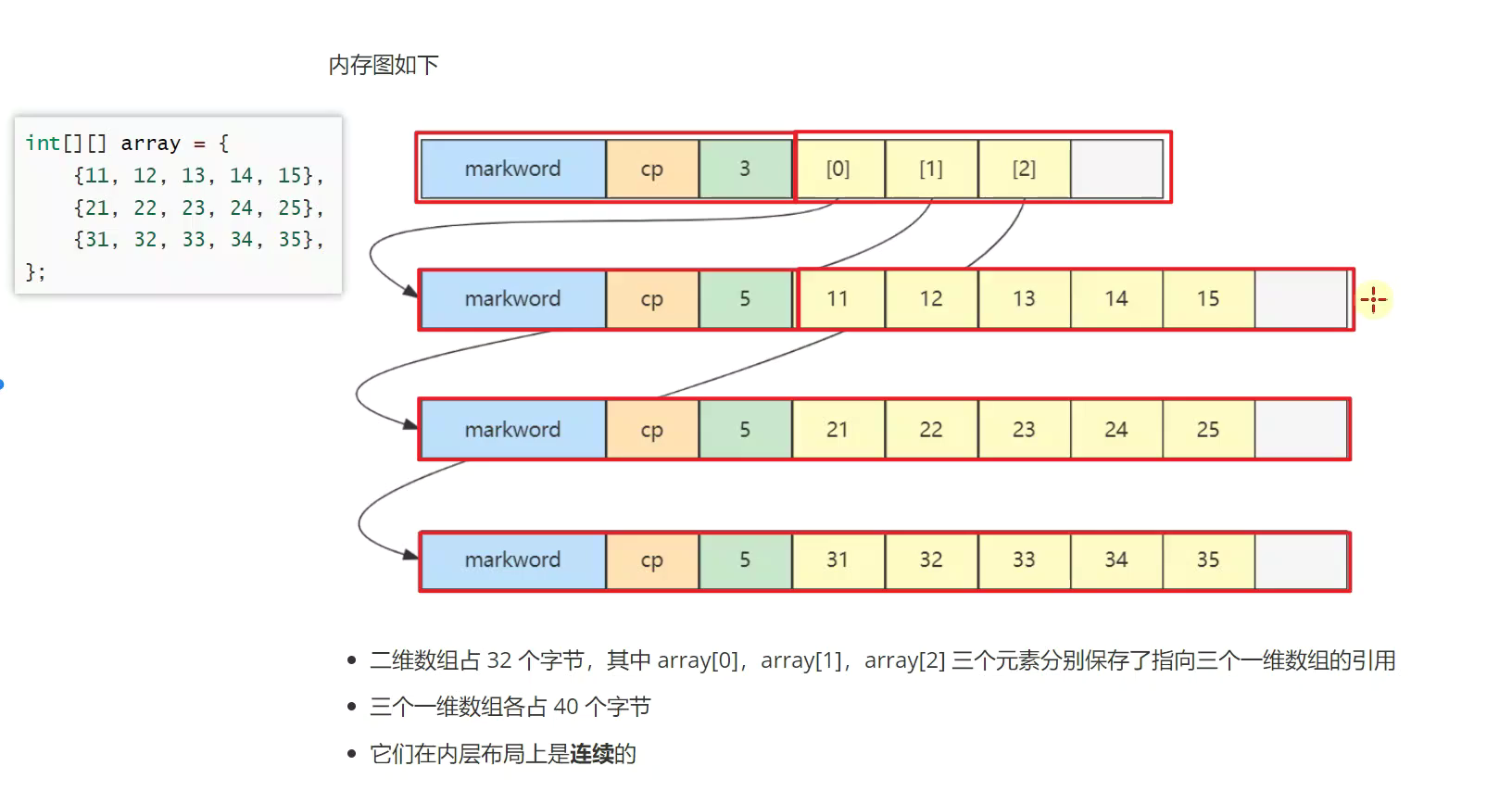
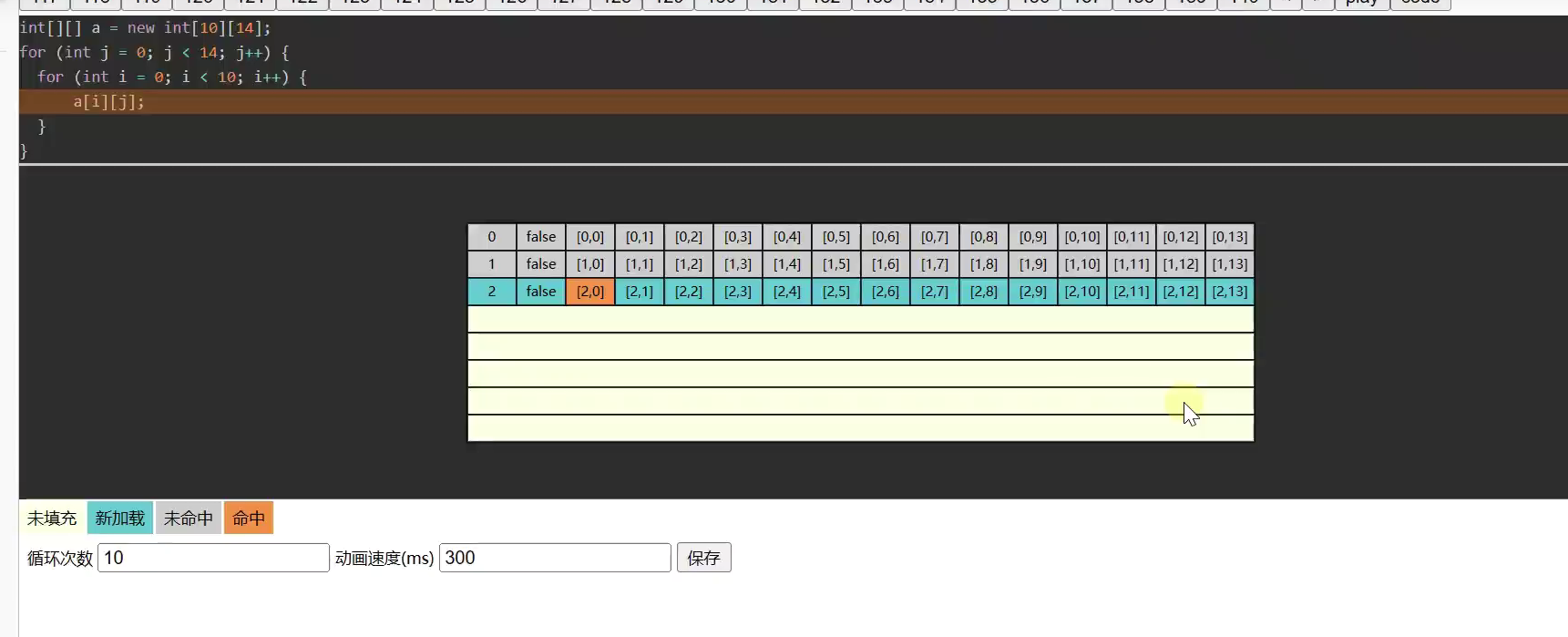
二维数组

两种遍历方式速度差异的原因
行列快于列行，因为缓存行
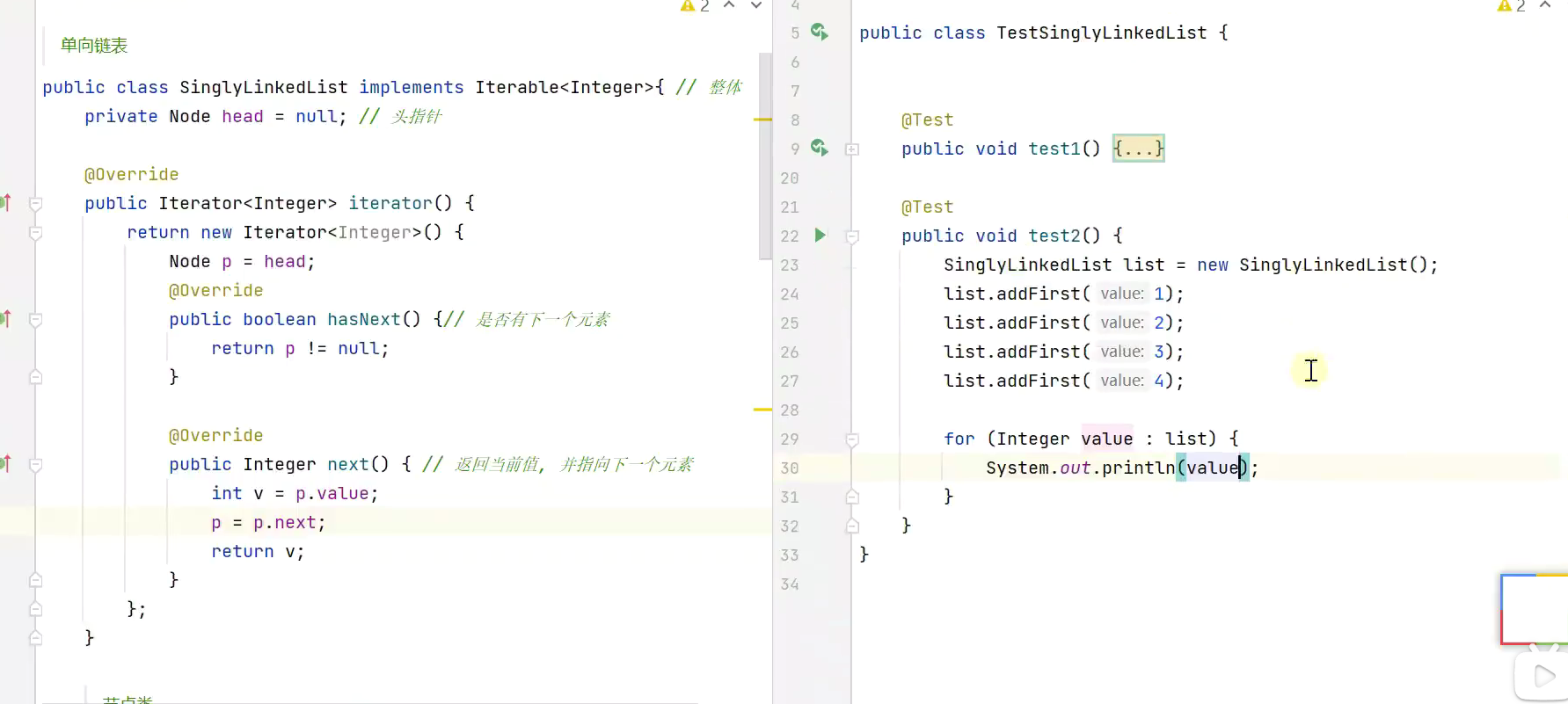
链表

迭代器遍历
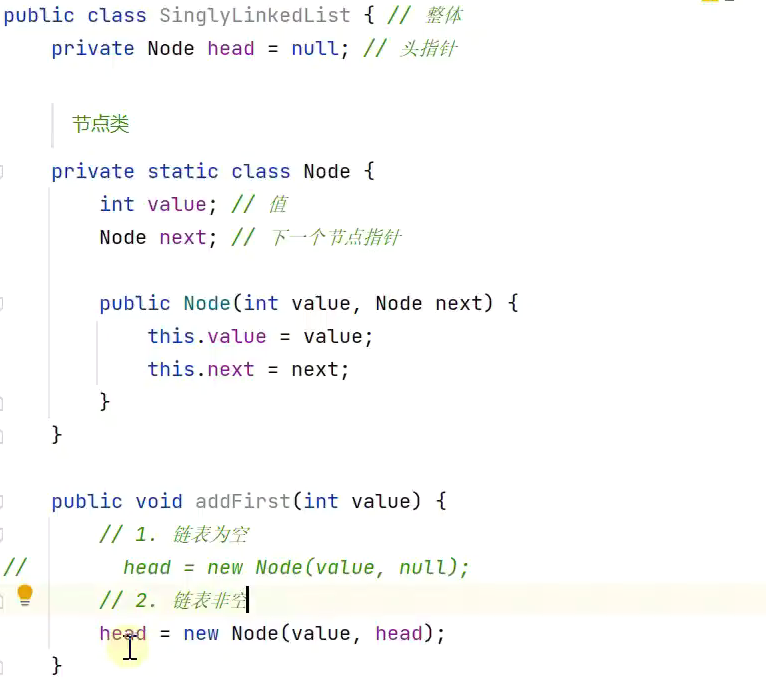
头部添加

尾部添加
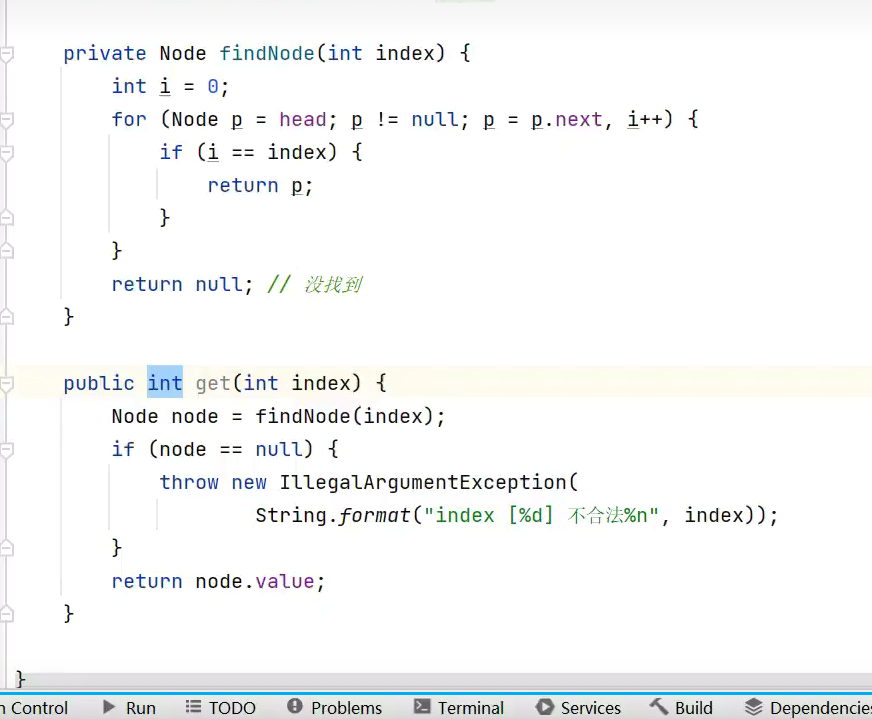
根据索引查找

根据索引位置插了入
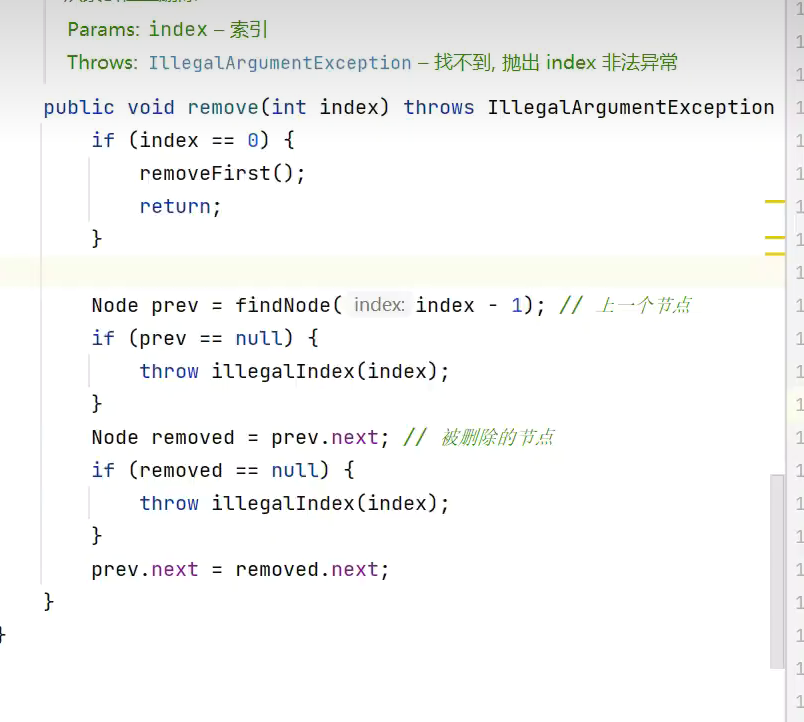
删除

递归冒泡排序

public class BubbleSort {

    public  static  void sort(int[] a){

        bubble(a, a.length-1);

    }

    //j代表未排序区域右边界
    private static  void bubble(int[] a ,int j){
        //设置递归调用的结束条件，防止递归调用陷入死循环
        if (j == 0 ){
            return;
        }

        //x代表有效边界，减少递归次数
        int x = 0 ;

        for(int i = 0  ; i < j;i++){
            if(a[i]> a[i+1]){
                int  t = a[i];
                a[i] = a[i+1];
                a[i+1] = t;
                x =i;
            }
        }
        //递归调用
        bubble(a,x);


    }

    public static void main(String[] args) {
        int[] a ={6, 5 ,4,3,2,1};
        System.out.println(Arrays.toString(a));
//        bubble(a,5);
        sort(a);
        System.out.println(Arrays.toString(a));

    }
}

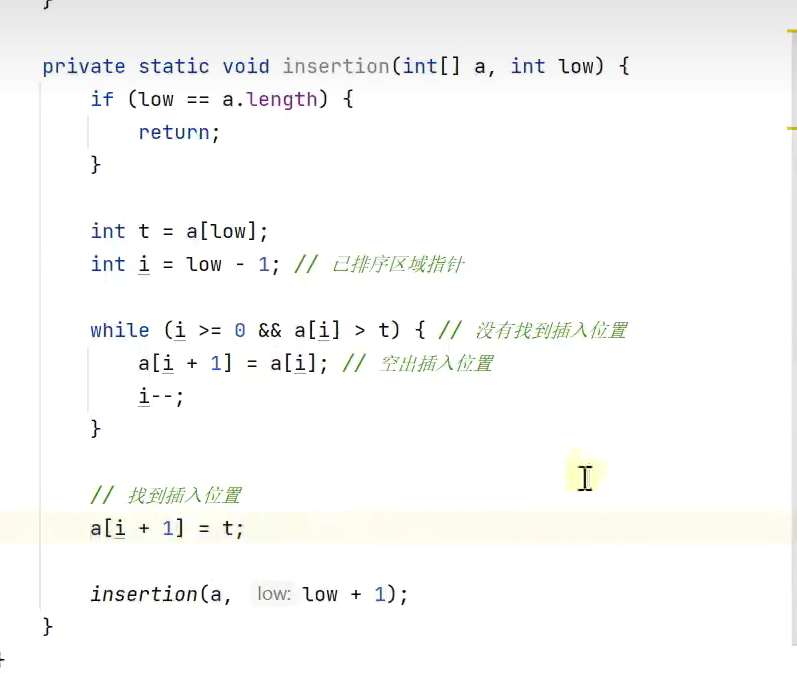
递归插入排序

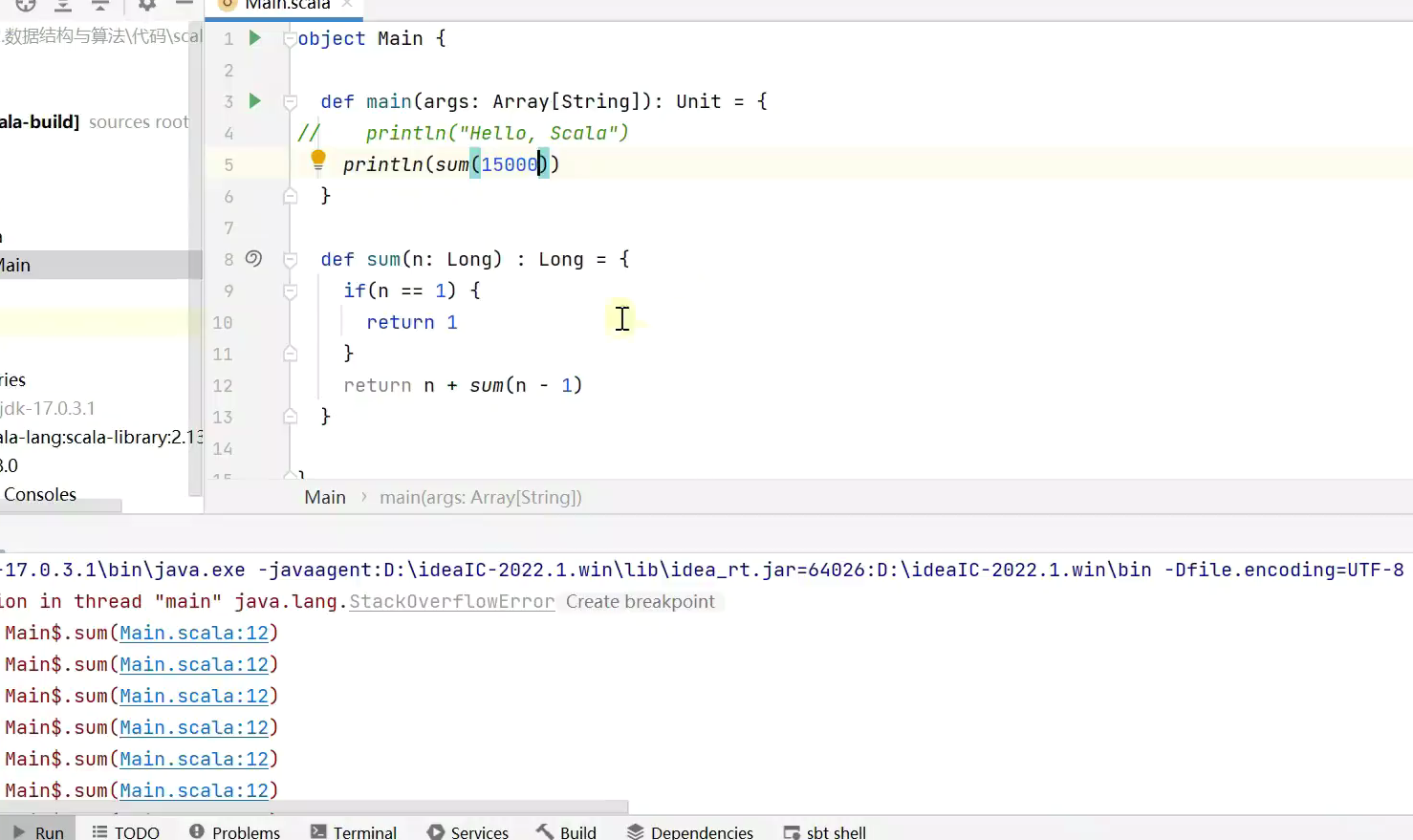
递归栈溢出
如何解决？
一、
尾调用
尾递归
scala

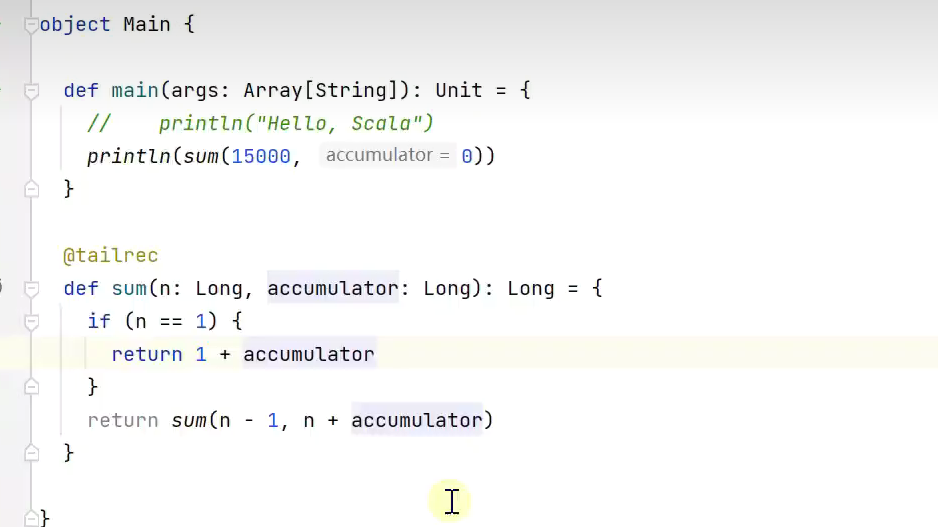
改写为尾递归

及时释放外层函数占用的内存

二、用循环代替

递归复杂度计算

主定理

展开求解

计算递归时间复杂度的网站

https://www.wolframalpha.com/
杨辉三角

使用二维数组暂存中间数据

每次递归前判断值是否已经计算过，存在二维数组中了
动态规划
使用一维数组优化，相比二维数组，进行了空间优化

不用递归
数组后值相加覆盖前值
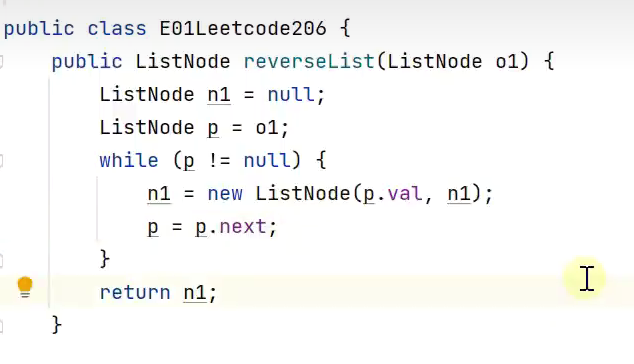
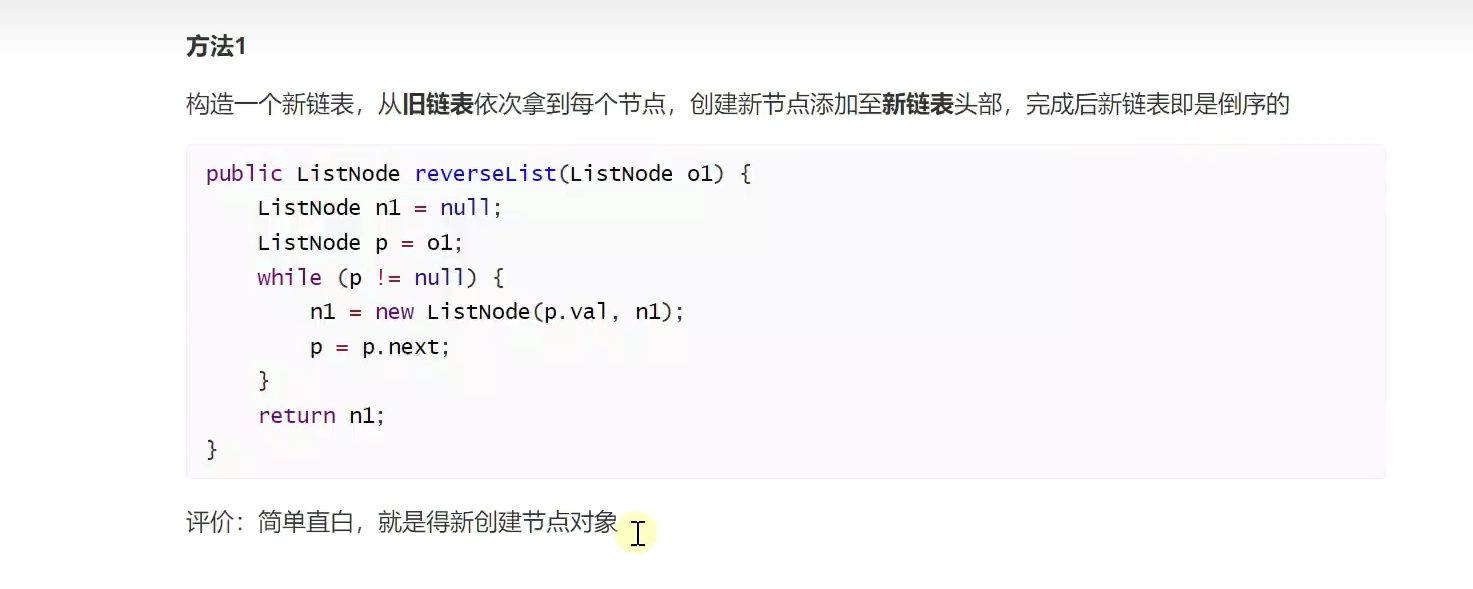
反转链表 /链表反转

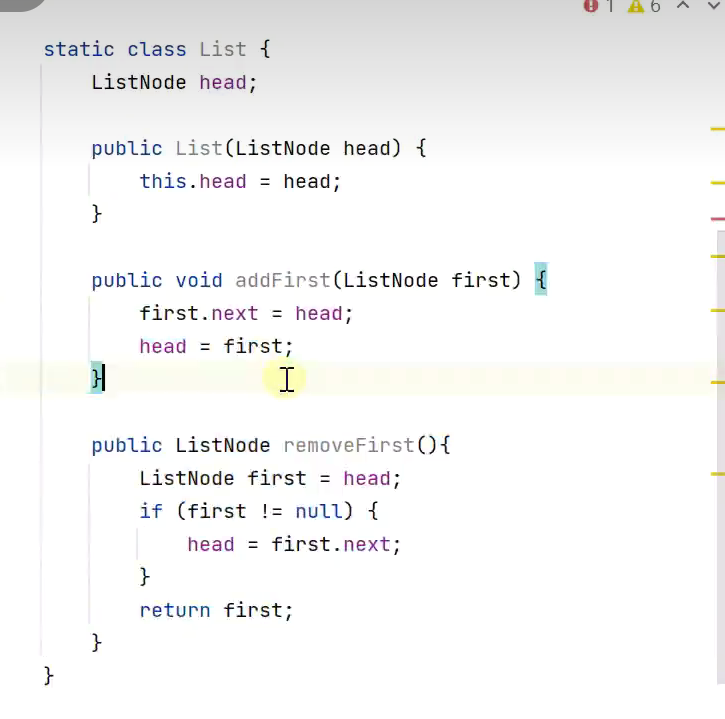
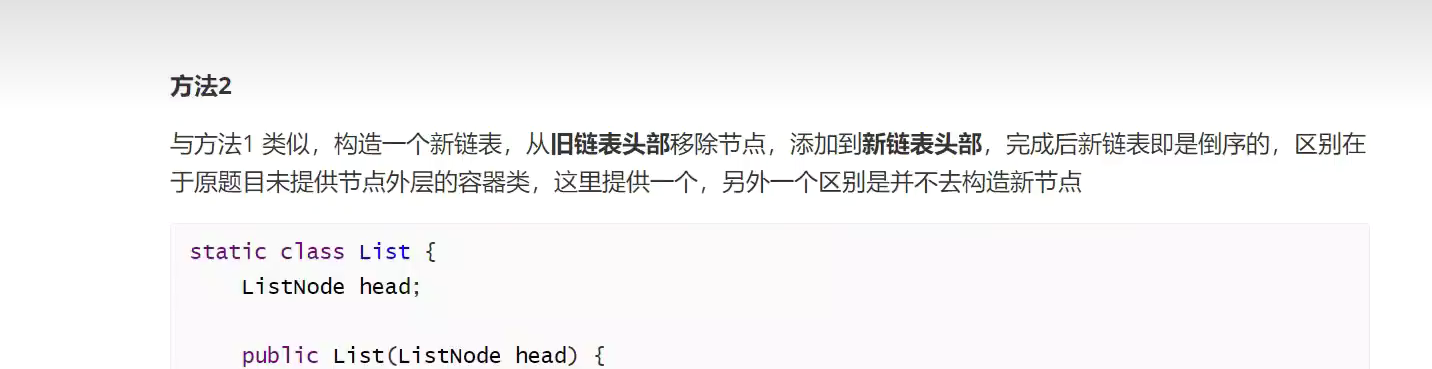
2.不用新建一个链表，利用外层容器类

法3 递归

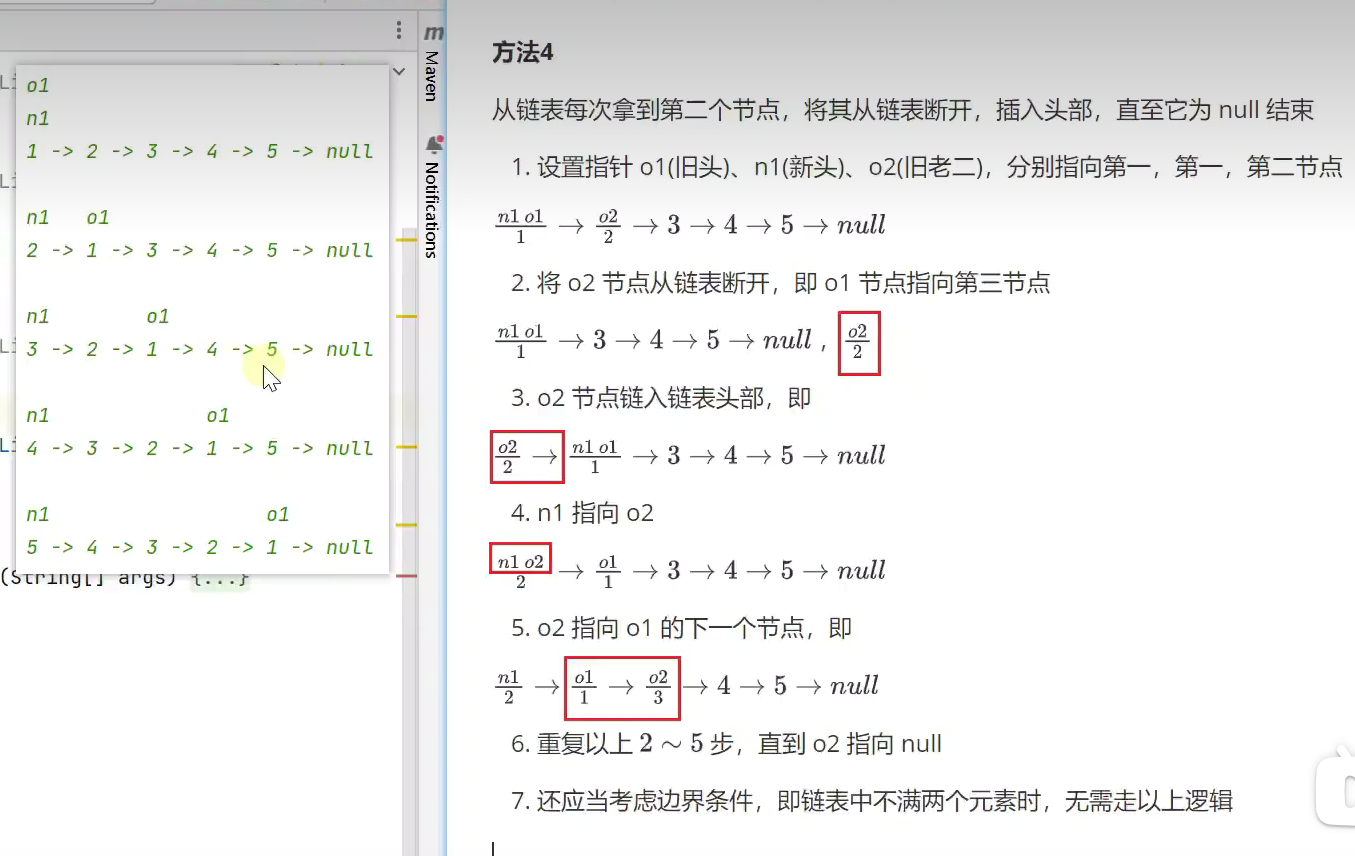
4.逐步挪动第二个的指针

核心代码

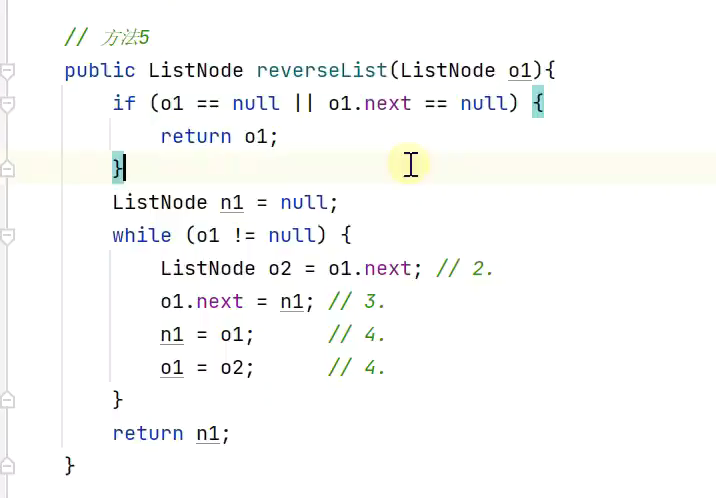
5.思路与法2一样，只是面向过程，直接在过程中实现

反转链表五种方法比较

法三
利用递归
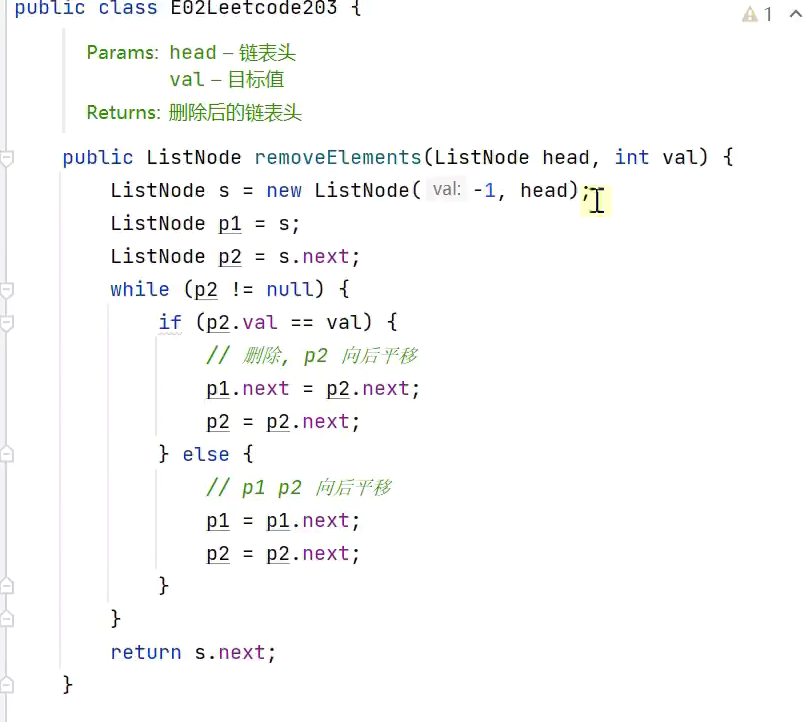
根据值删除节点

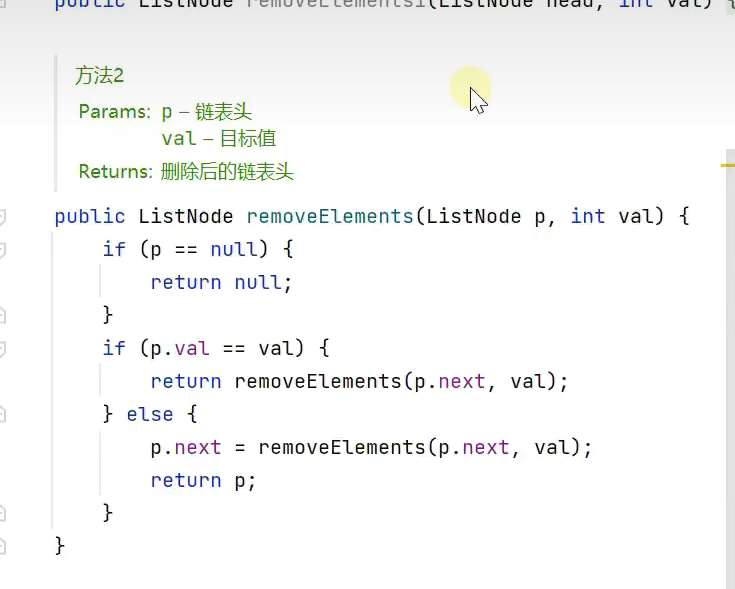
递归删除
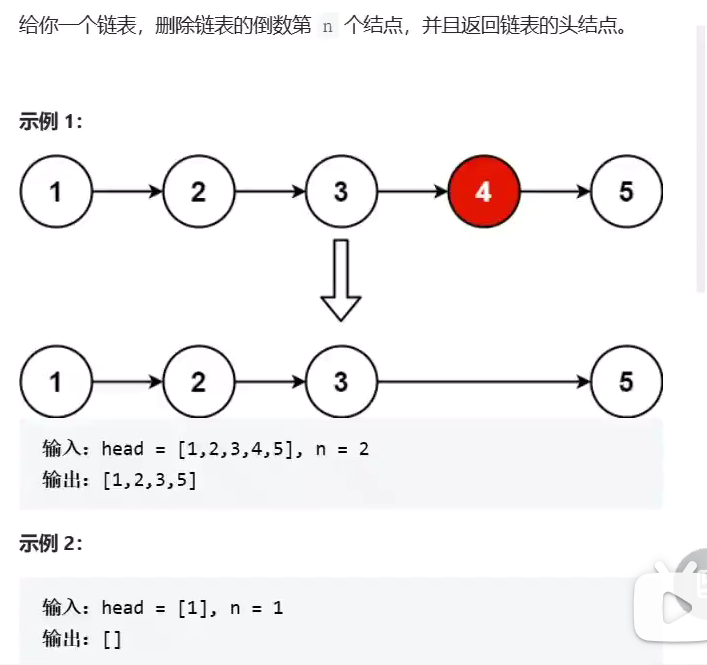
记录下一个结点的倒数位置

1.递归删除
用头节点保证第一个位置（倒数最后一个位置）可以被正常删除

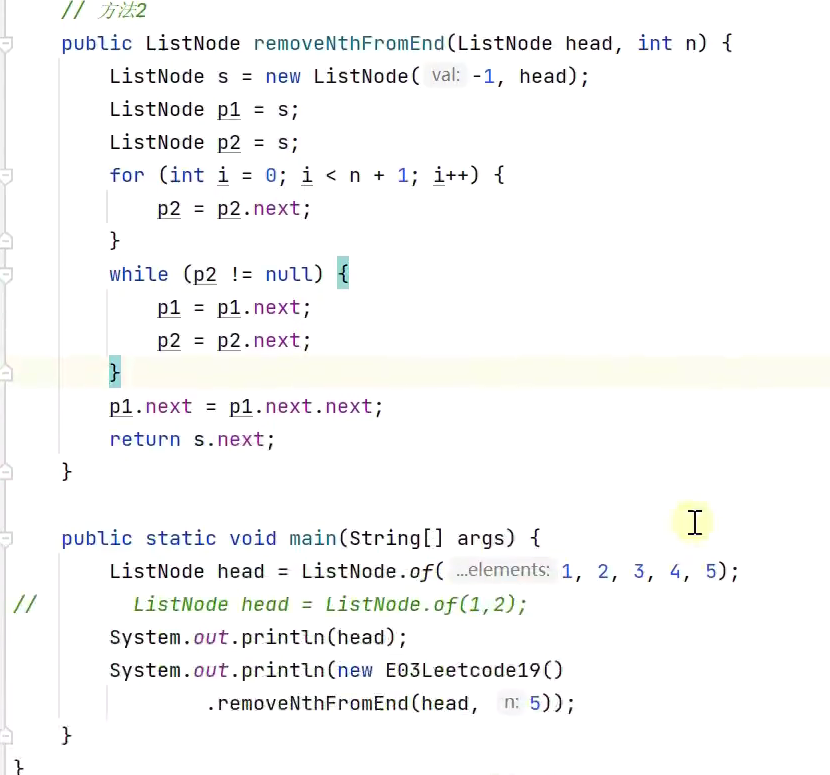
2.快慢指针法
有序链表删除重复元素，保留一个

1.双指针

2.递归
有序链表去重，重复元素一个不留

2.非递归，指针
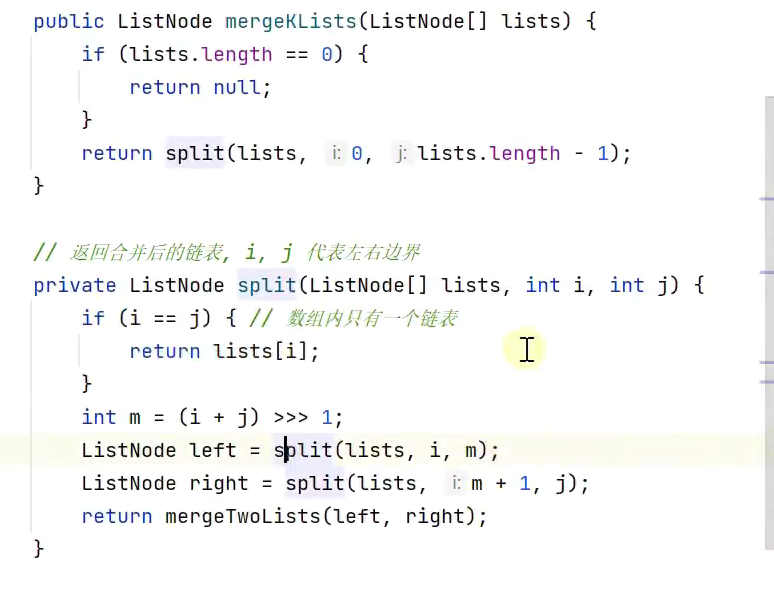
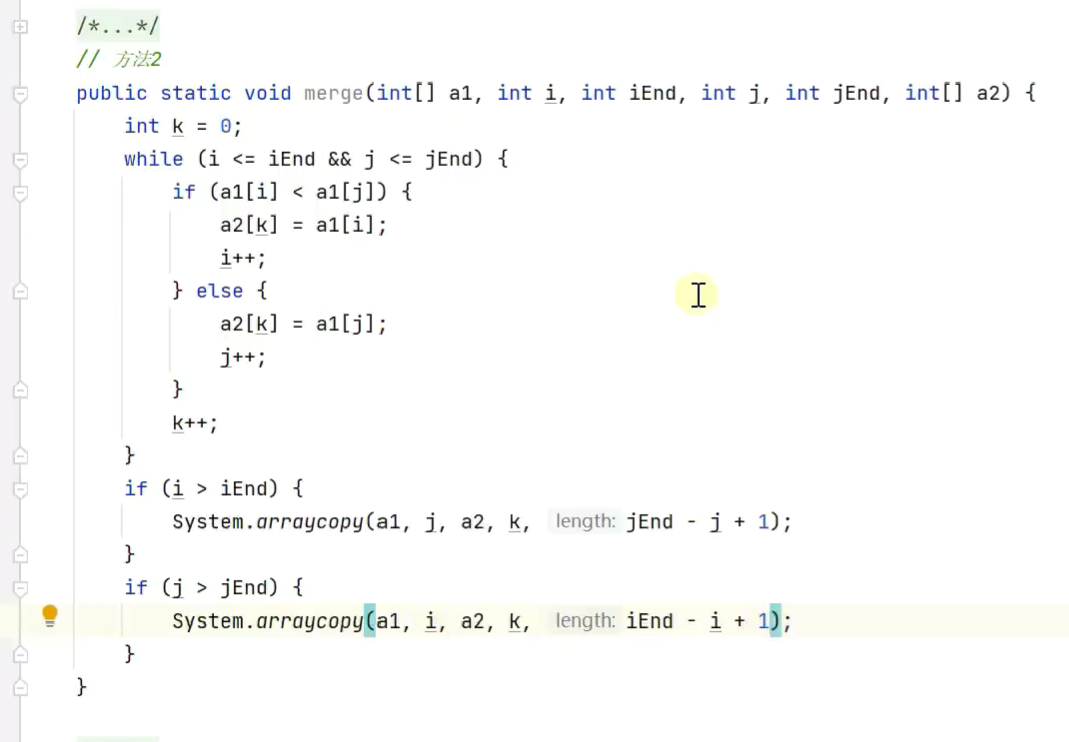
合并有序链表
拆分
查找链表中间节点

1.快慢指针
一个指针一次走一步
另一个指针一次走两步
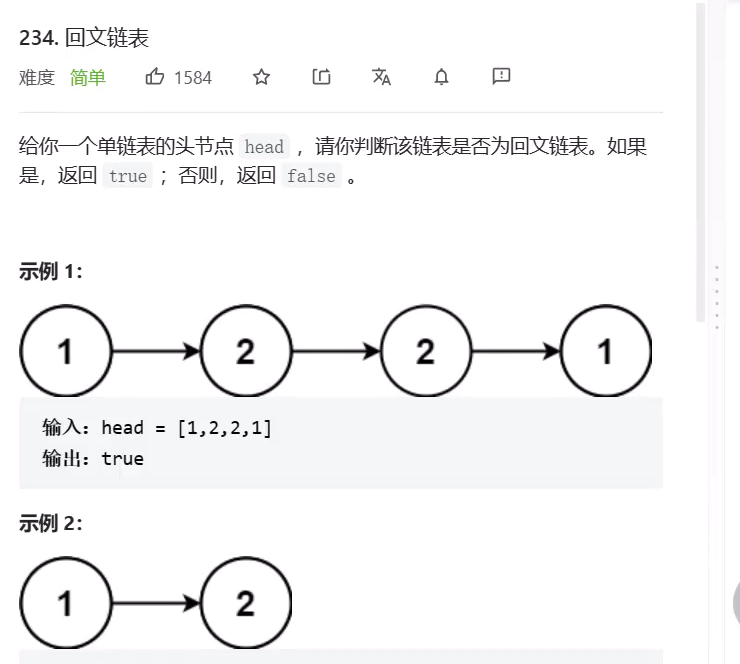
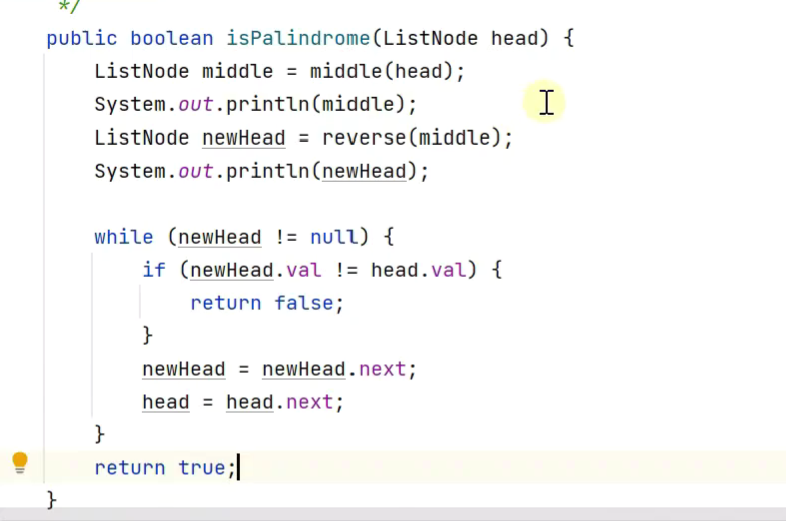
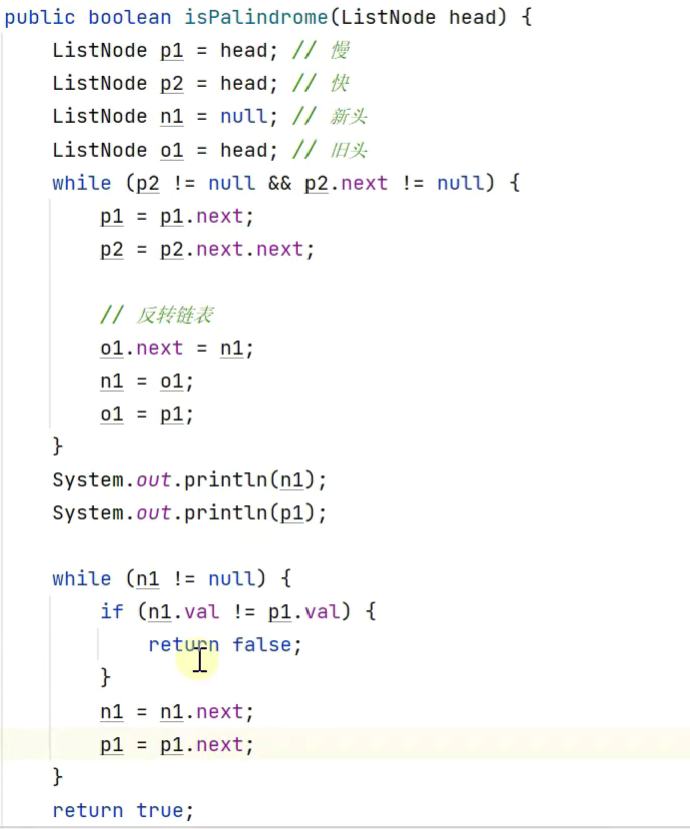
判断回文链表

寻找中间节点用快慢指针法
反转用之前的链表反转方法，下面用的第五种方法

将其他方法的代码合并到一个方法中

优化：将前两步放在同一个循环中

因为o2与p1同步移动，每次移动一步，所以可以用p1代替o2赋给o1

上面的代码在奇数节点链表时会出错

加入
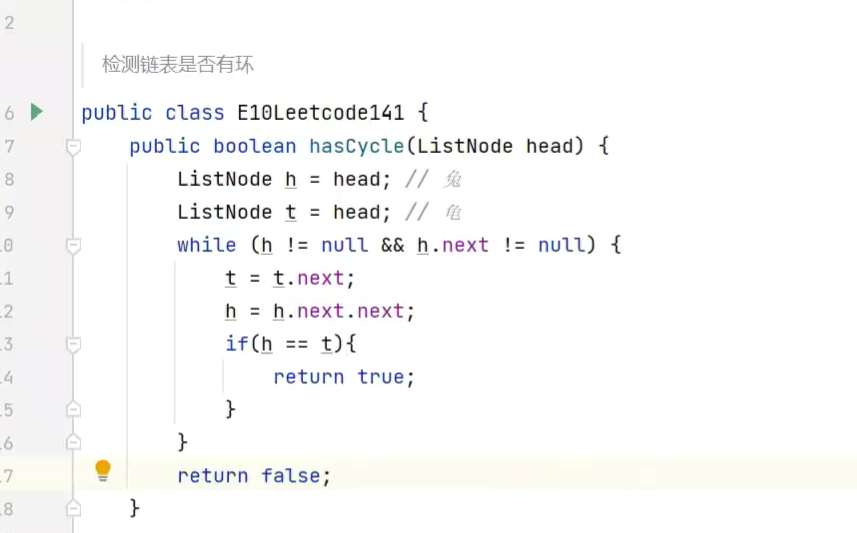
检测链表中是否有环

算法：弗洛伊德龟兔算法

1.判断是否有环

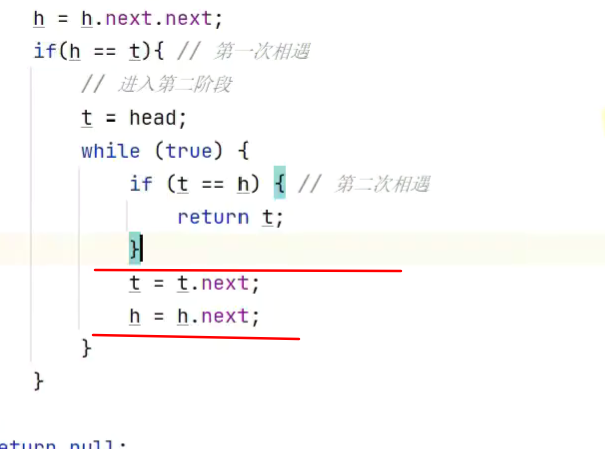
2.若有环，找出环的入口

缺点：无法判断首尾相接的环
改进
先判断再前进
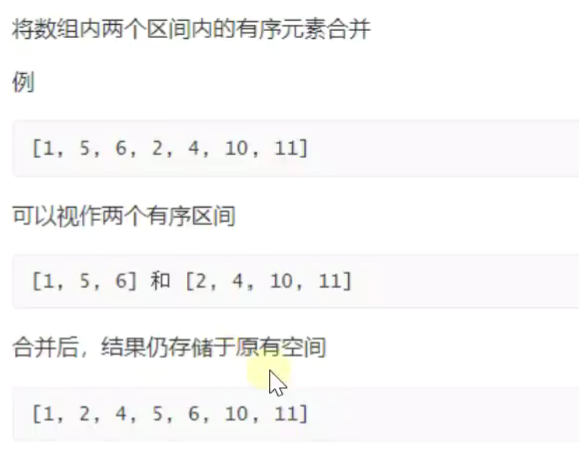
合并数组

递归

2.非递归
指针
分而治之
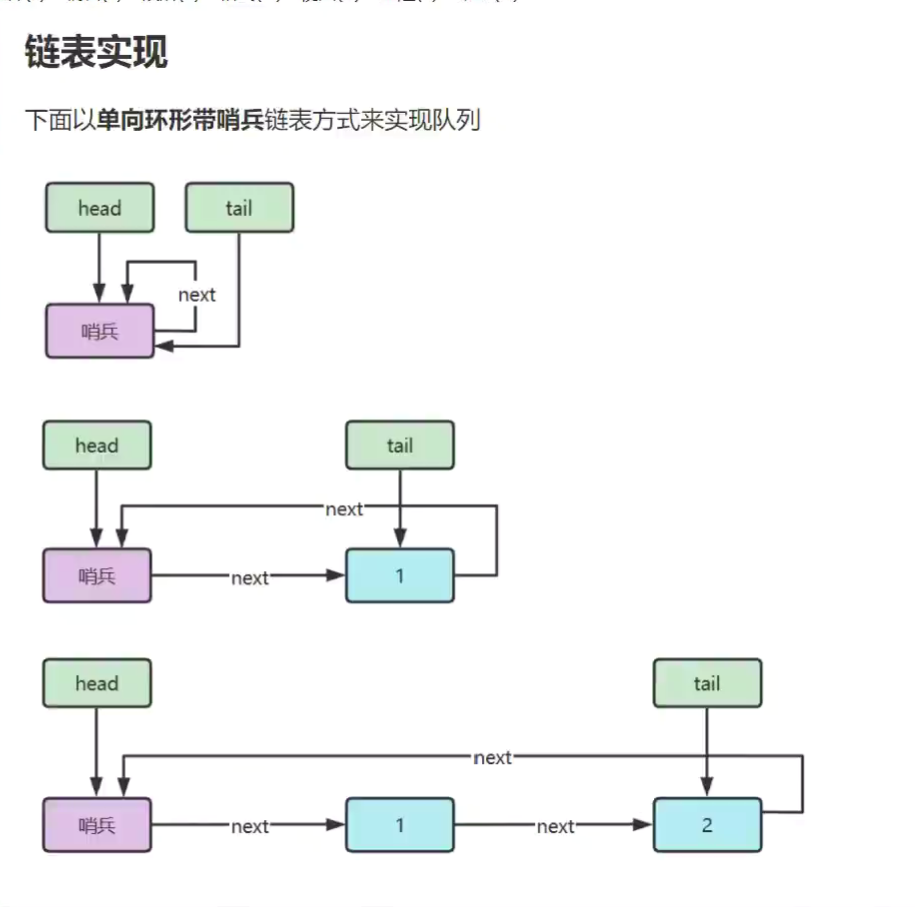
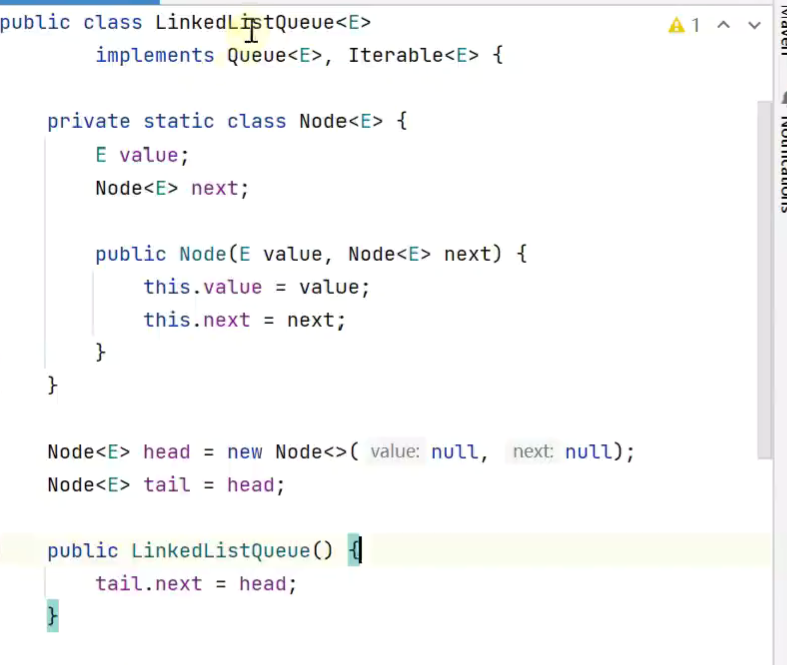
队列
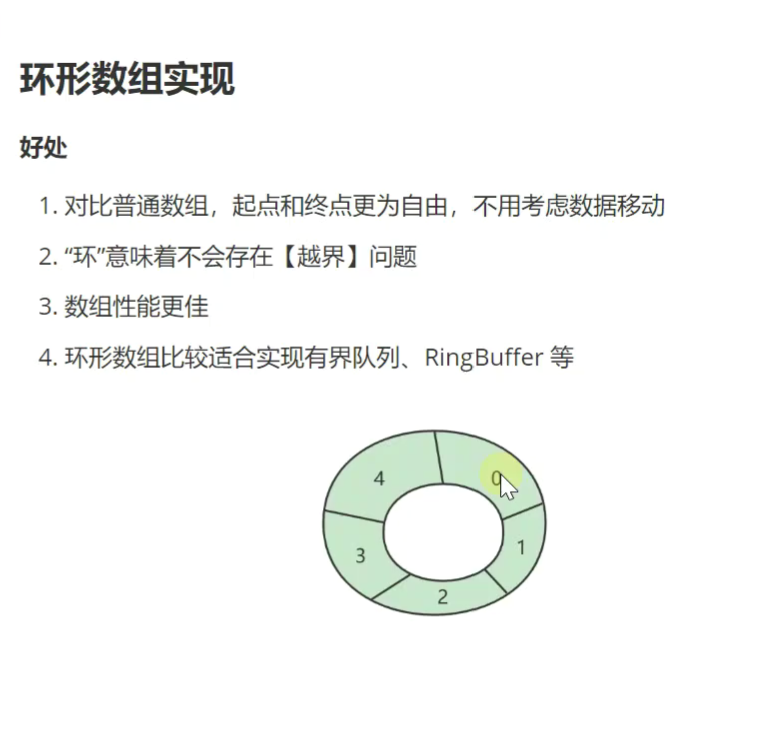
环形数组

相比普通数组，删除效率更高，时间复杂度低。任意一个位置都可以作为头和尾

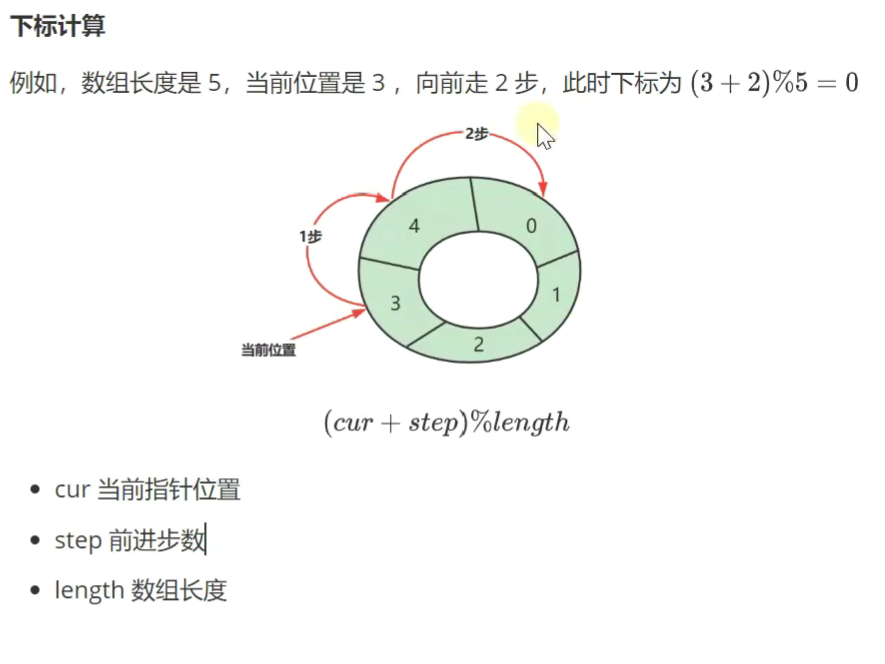
1.如何计算下标和索引

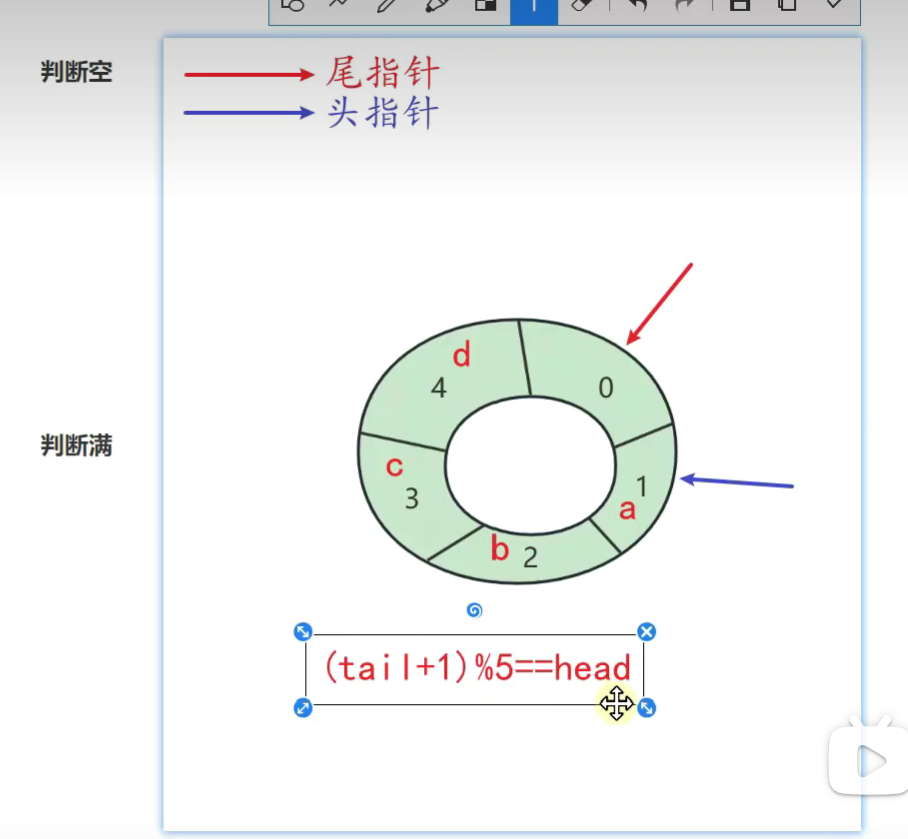
如何判断空和满
和环形链表类似

缺点：有一个为空

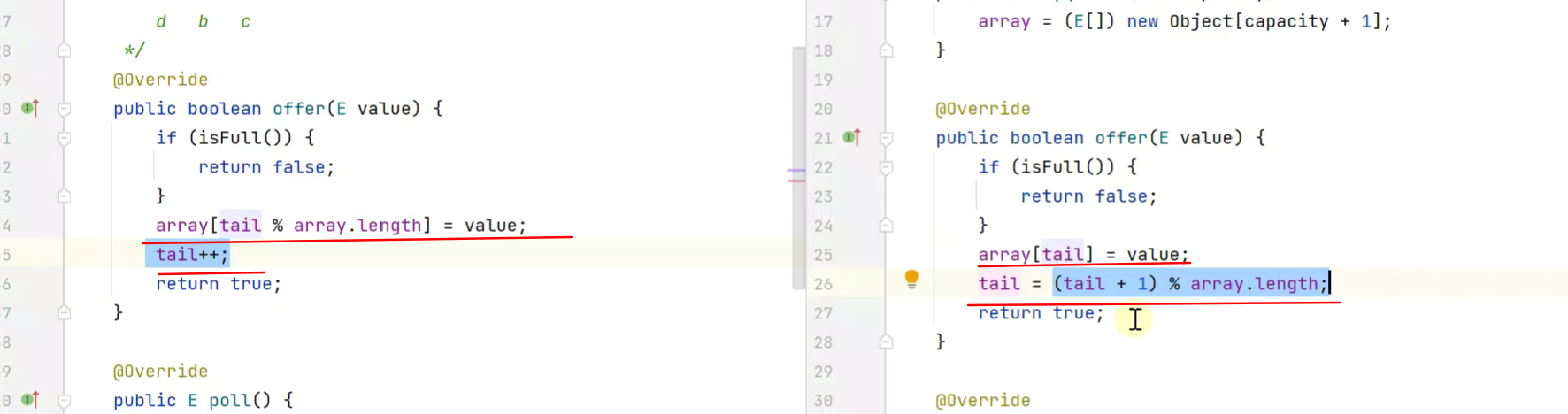
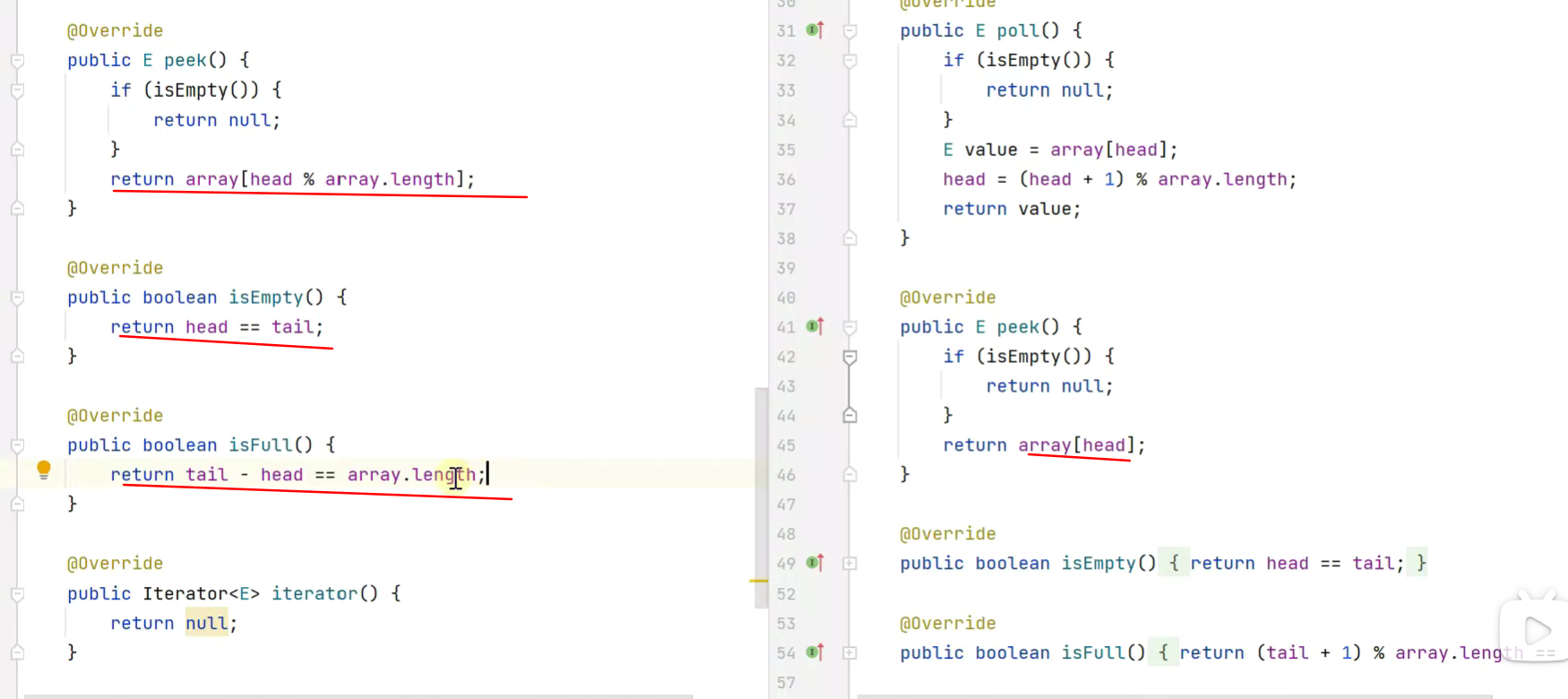
改版：引入一个新的变量size记录数组的元素个数
Pro

head和tail为不断递增的证整数，不直接记录索引值，需进行运算后（mod数组长度）得出索引值、

对比

与右移后的结果进行逻辑或
二叉树

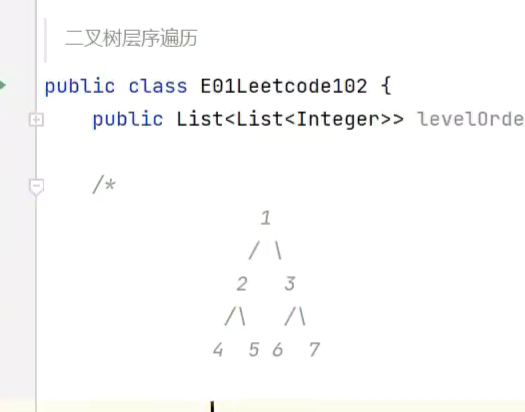
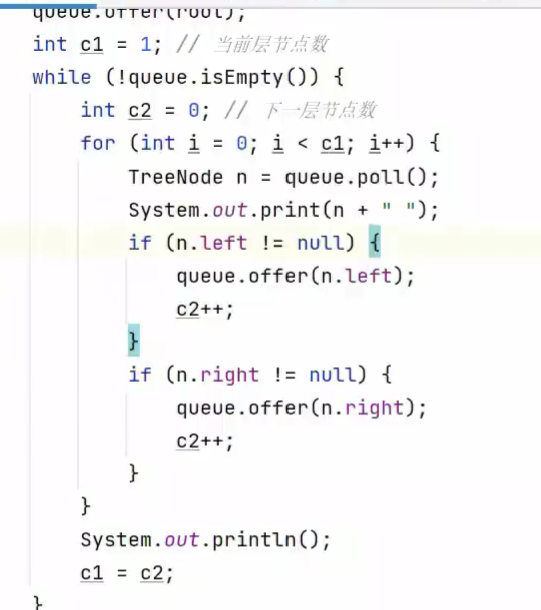
分层遍历

返回一个集合
栈

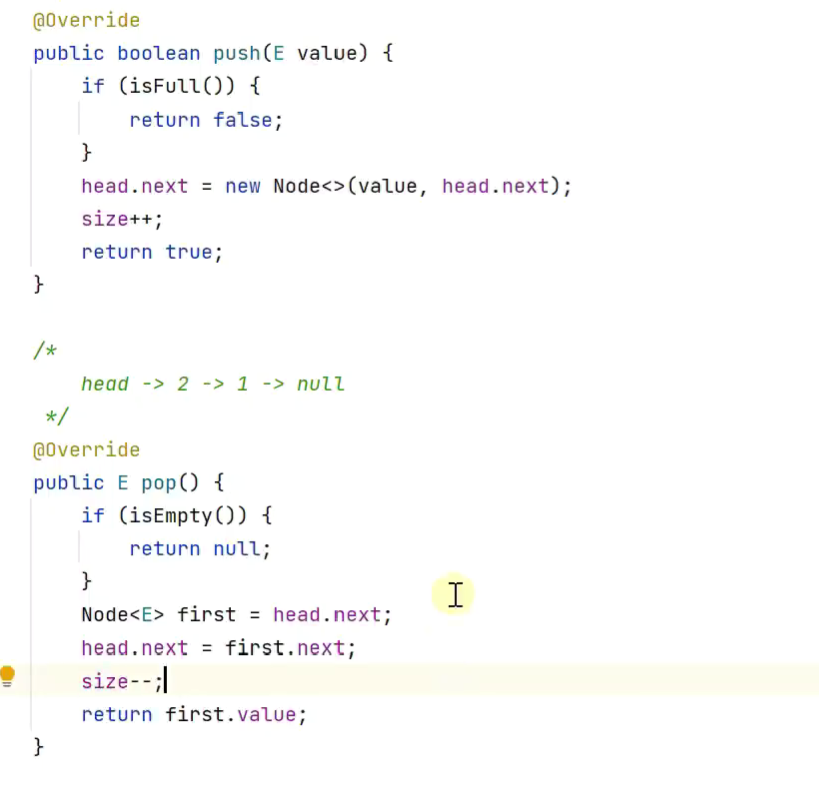
1.链表栈

2.数组栈
顶放在右边是因为数组右边添加和删除的效率较高
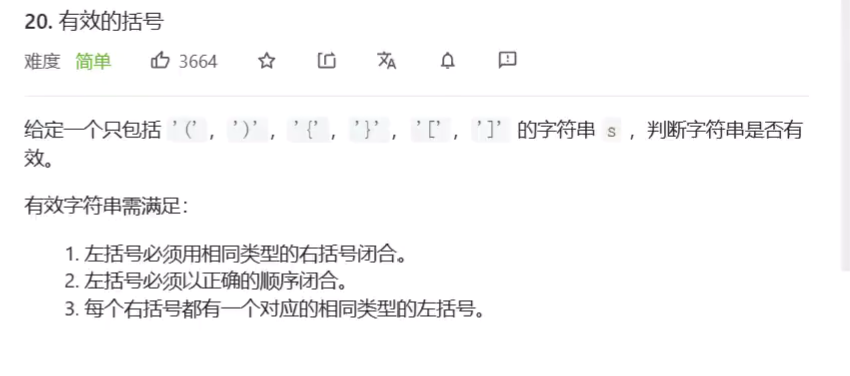
判断有效的括号，即括号成对以正确的顺序闭合

栈空则为true
逆波兰表达式求值后缀表达式
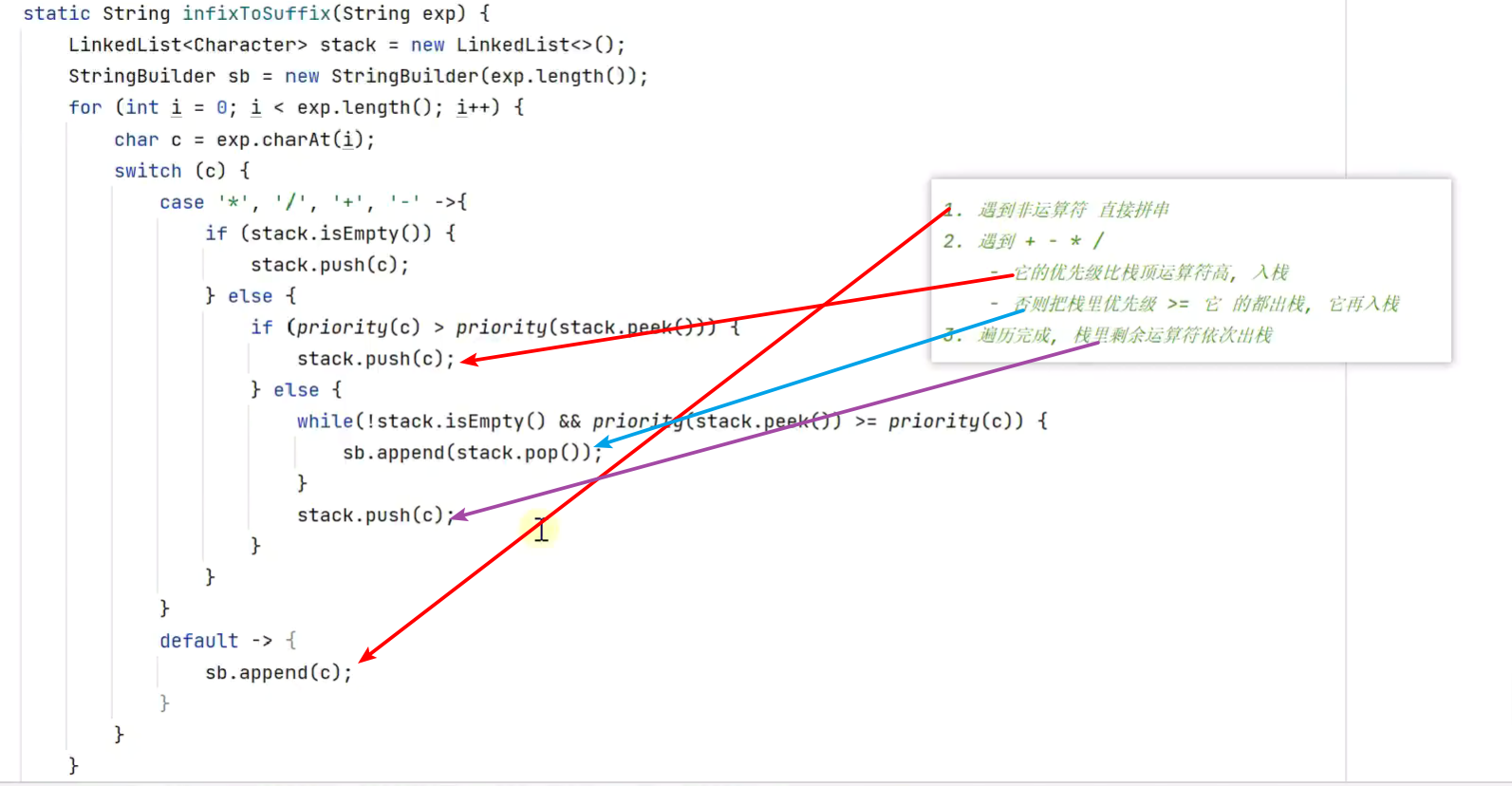
中缀表达式转后缀表达式

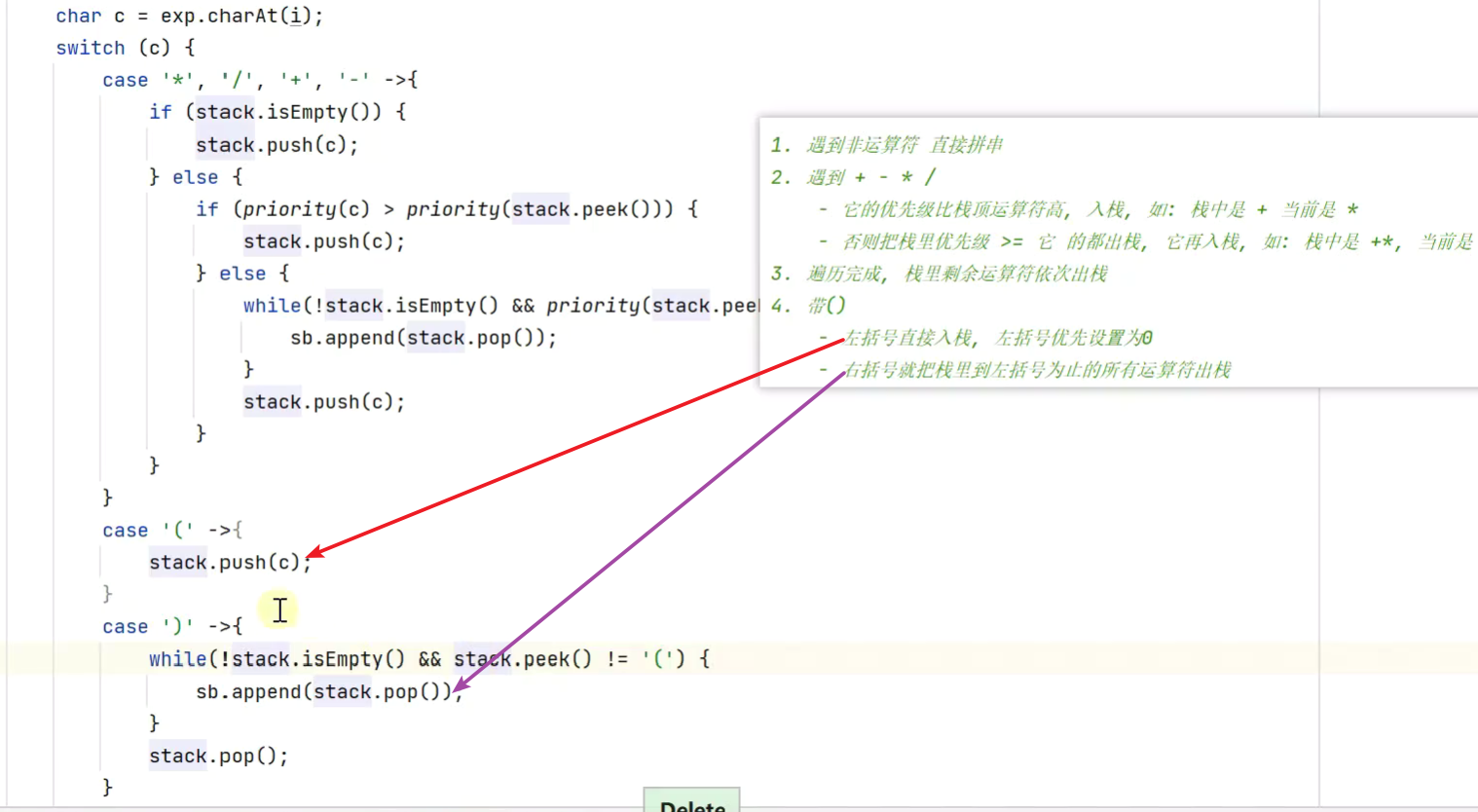
有小括号的情况
注：将（优先级设置低于+-
用两个栈模拟队列
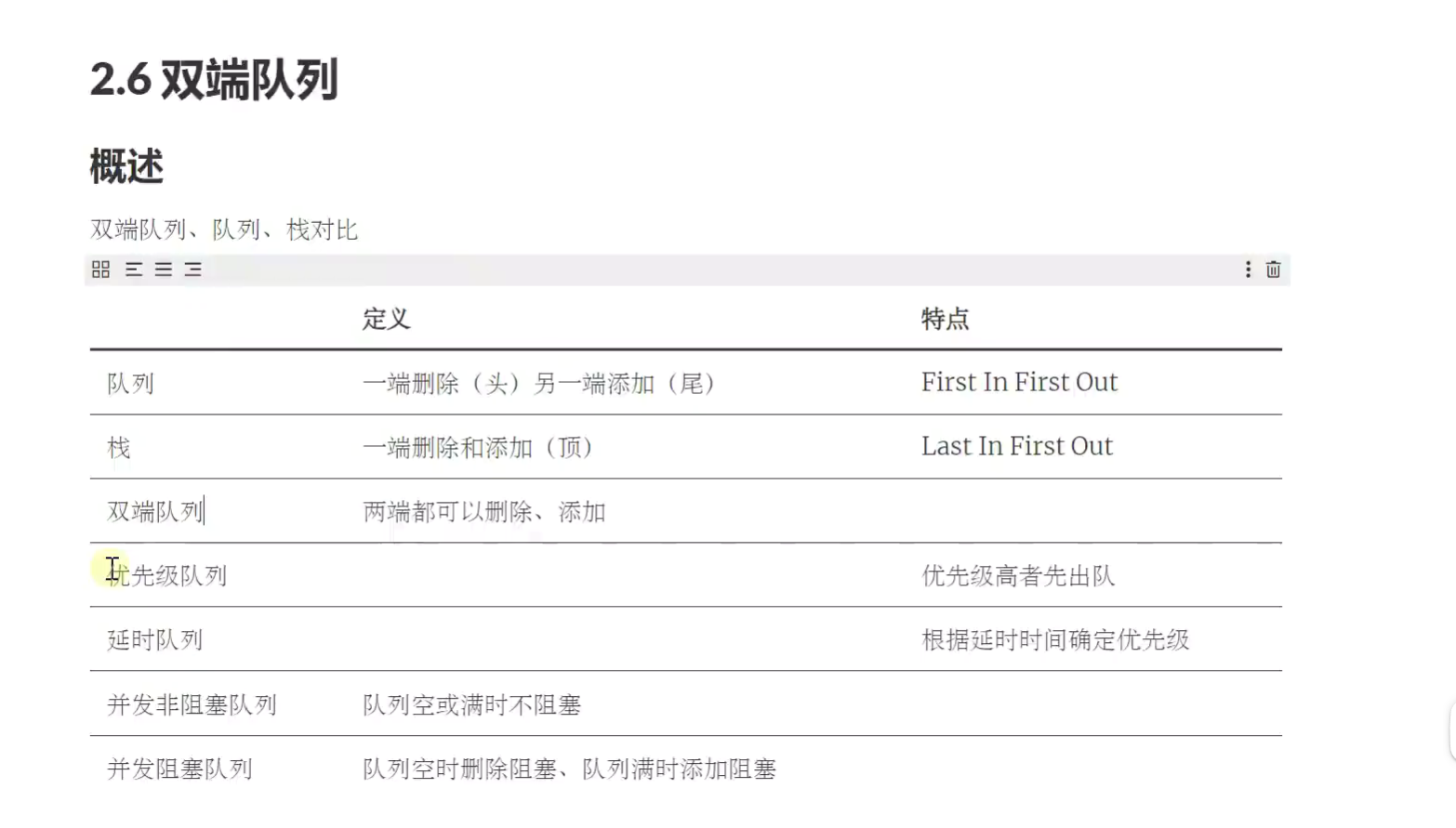
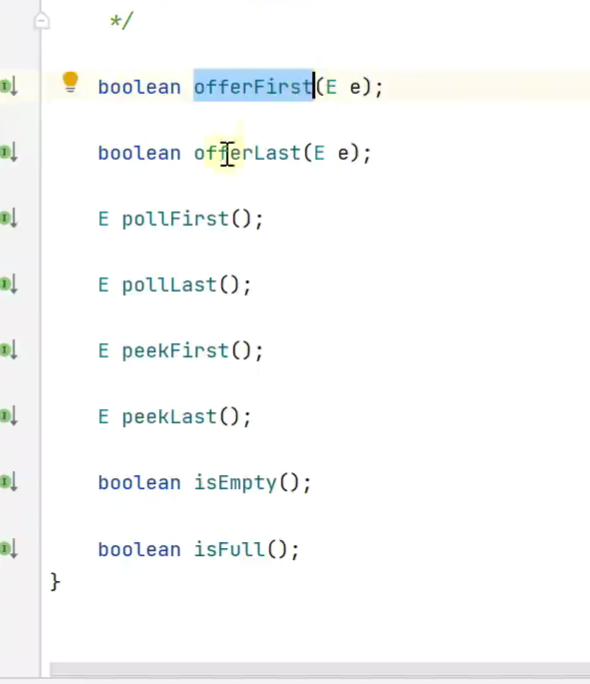
双端队列
Deque
double ended

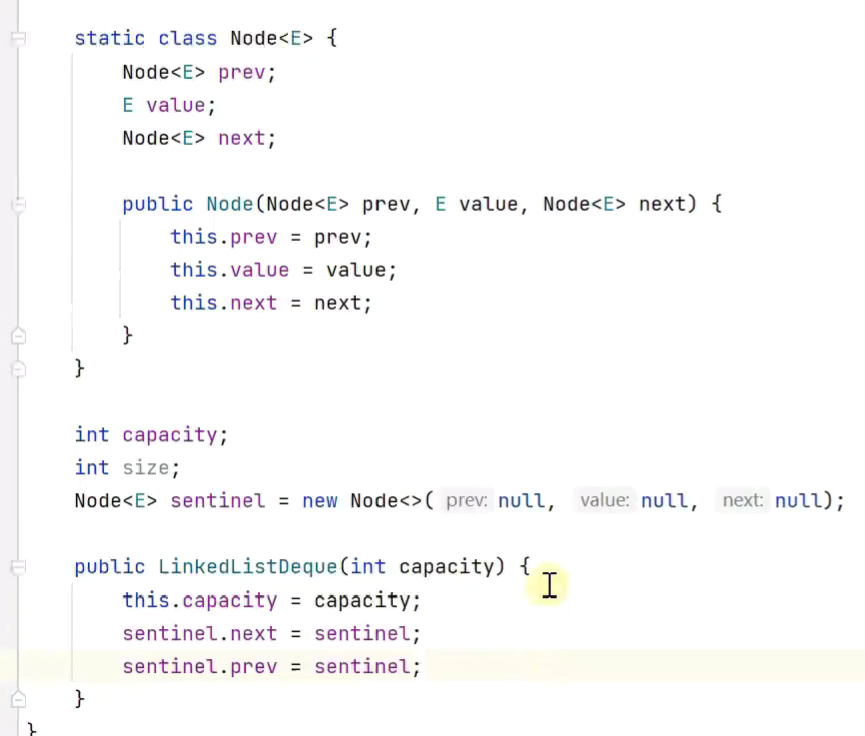
1.基于双向环形链表实现双向队列
使用环形可以让一个哨兵节点既充当头又充当尾

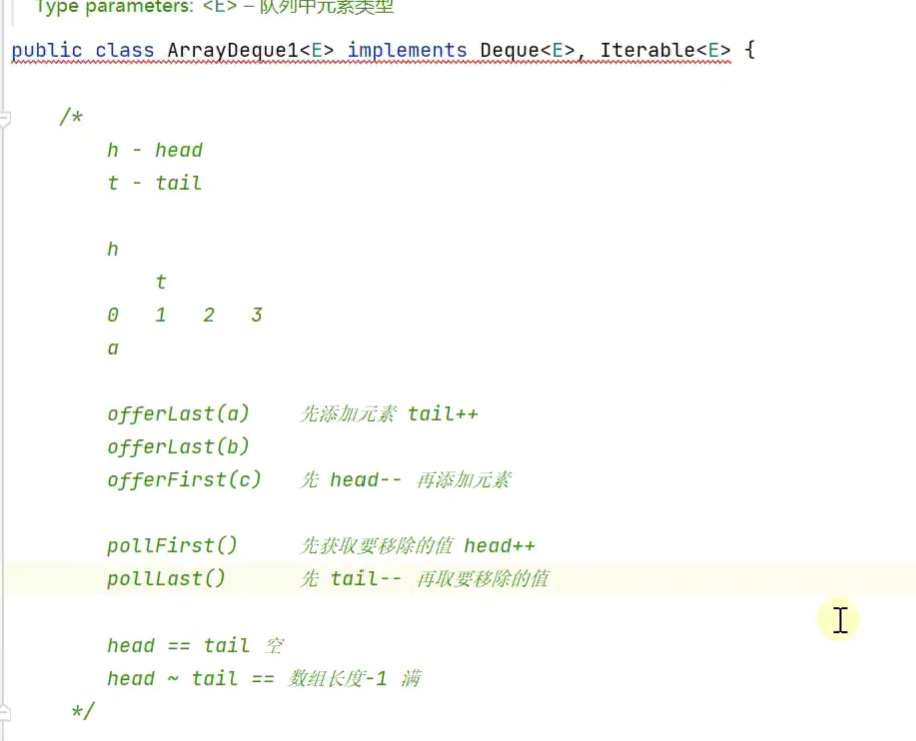
2.基于循环数组实现

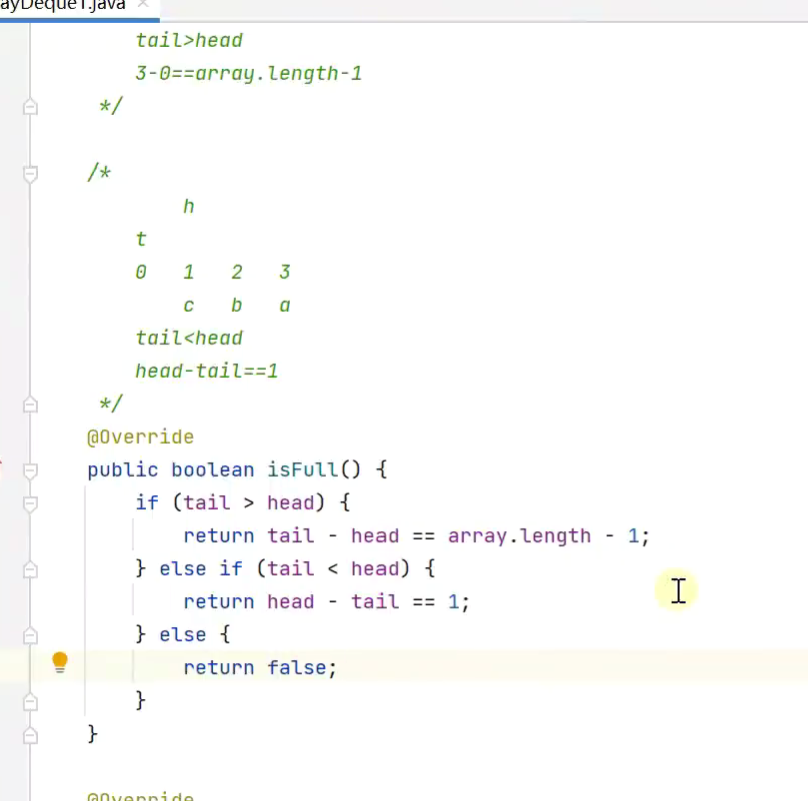
判断队满

头添加尾添加

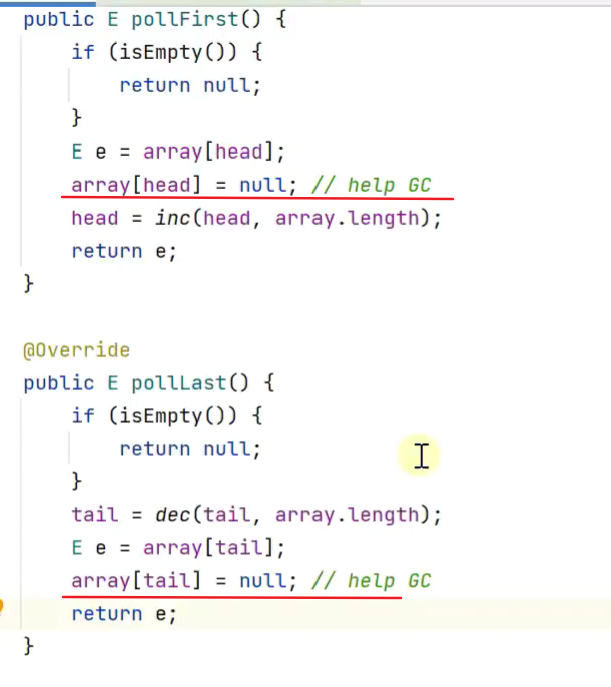
考虑内存释放
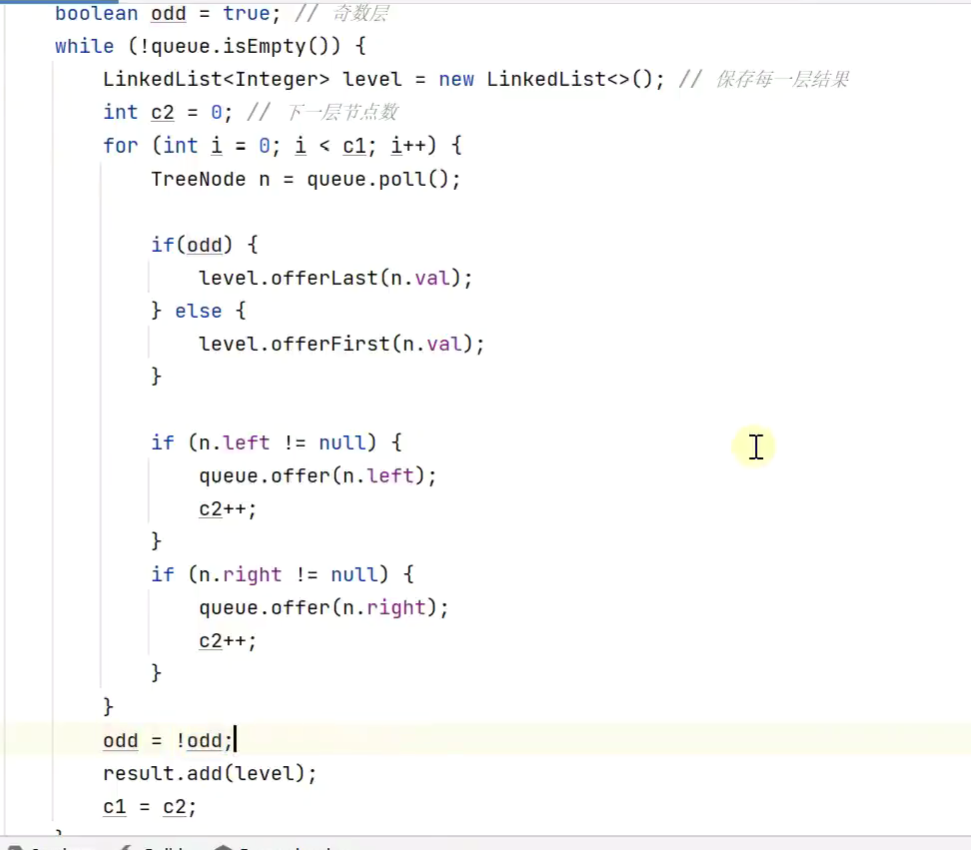
二叉树S形遍历
（走蛇形）
优先级队列

按照优先级出列

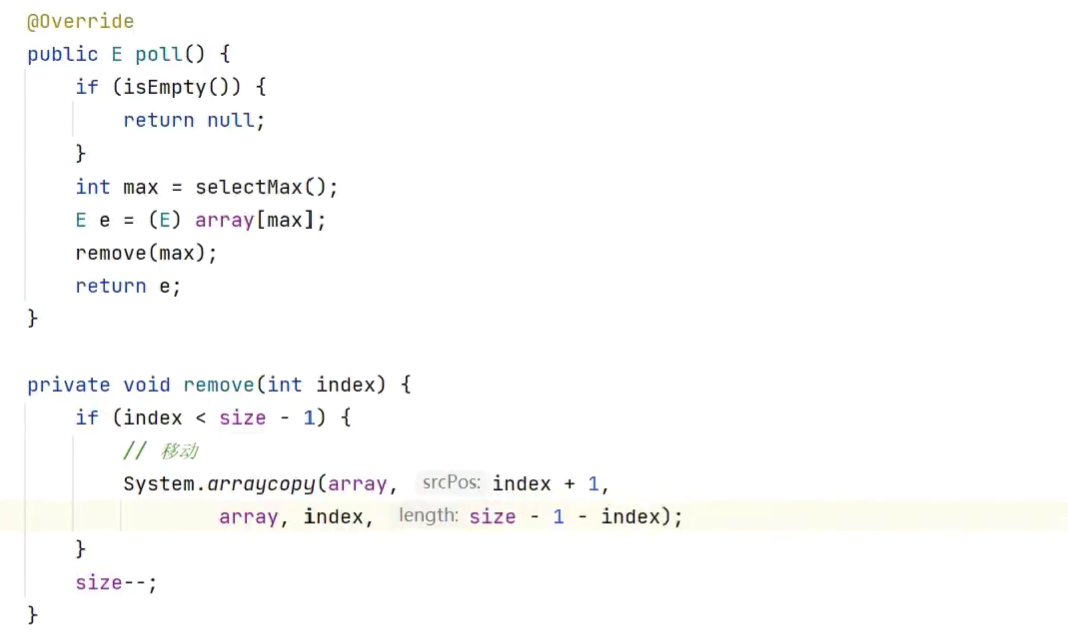
1.基于无序数组实现

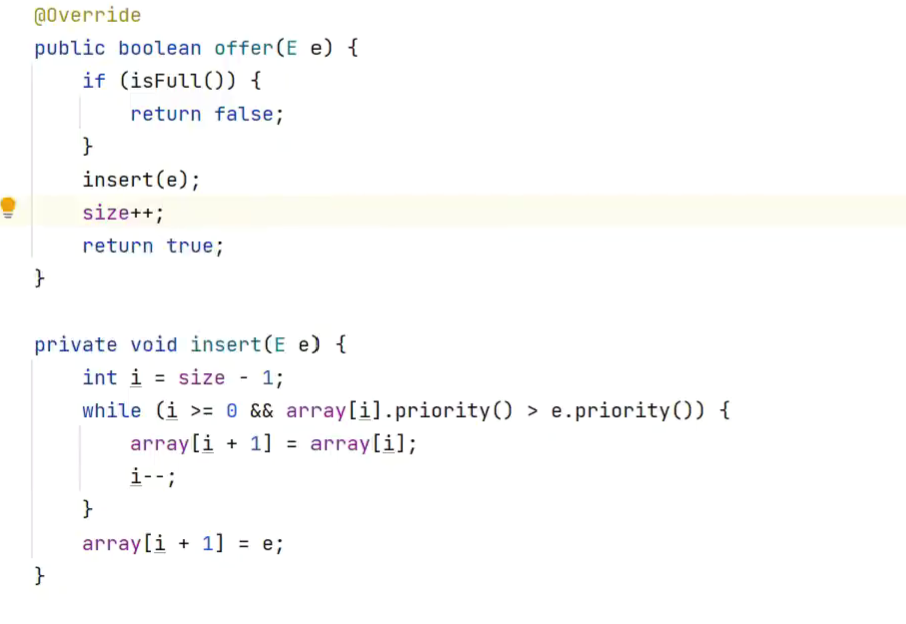
2.基于有序数组实现

入队使用插入排序

相比无序，入队复杂度高，出队复杂度低

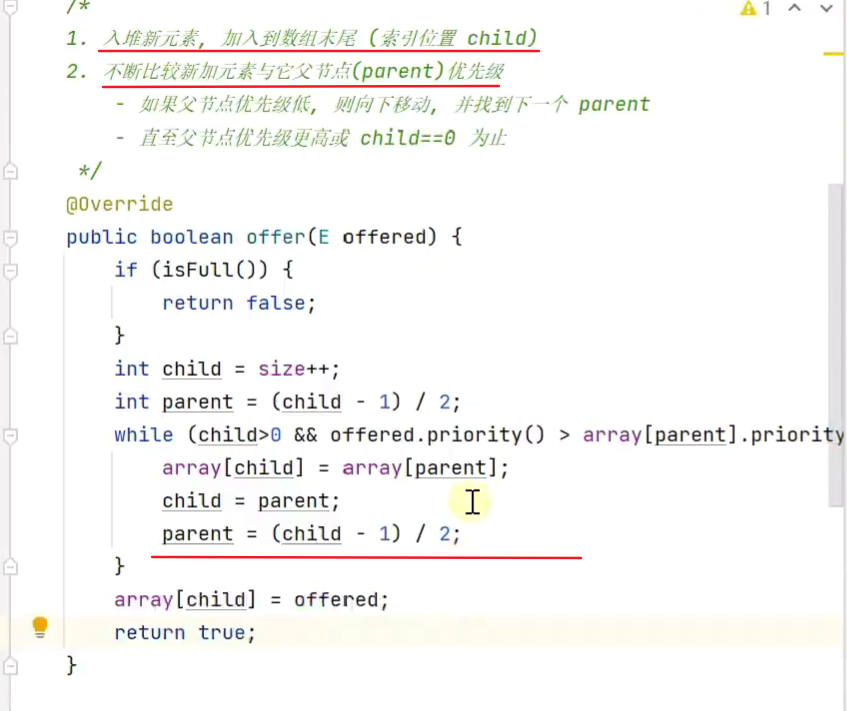
3.堆实现
完全二叉树
除最后一层可不填满其余均要填满

入队新元素

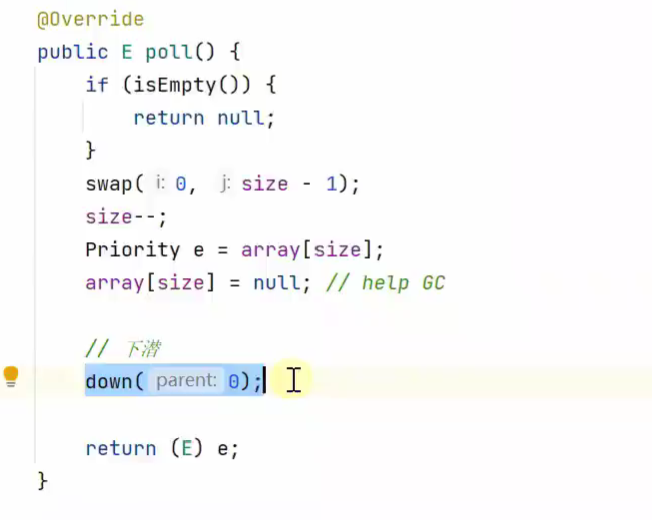
出队（交换、出队、下潜）

堆顶是最大的，即优先级最高的

出队

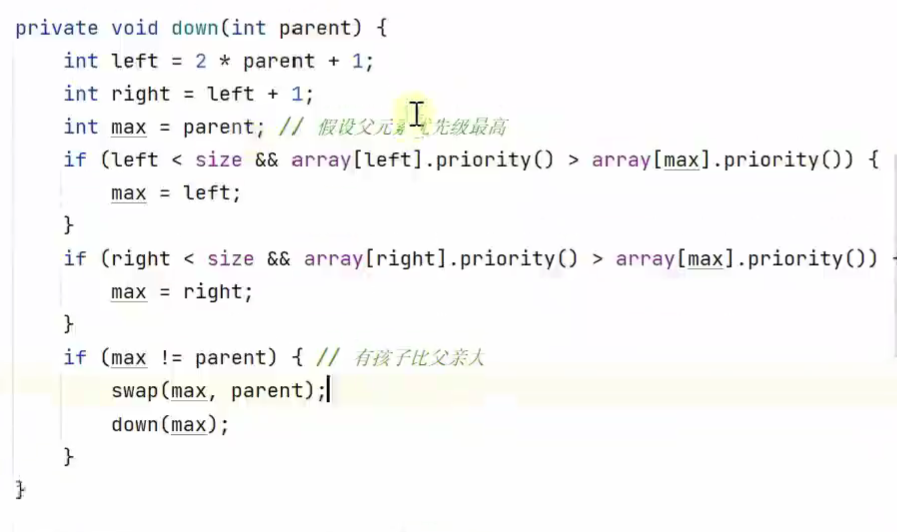
下潜
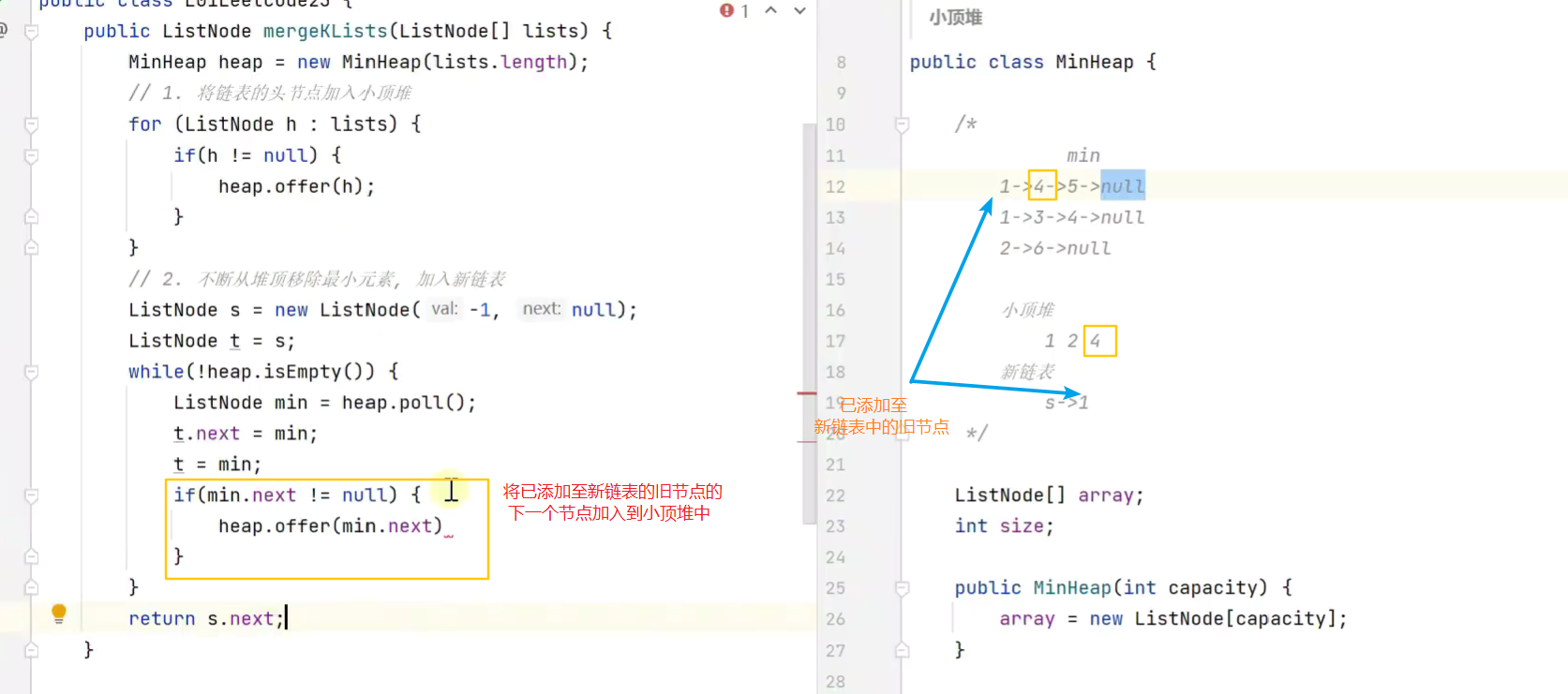
利用堆实现合并k个有序链表

小顶堆优先队列

miniHeap

合并链表

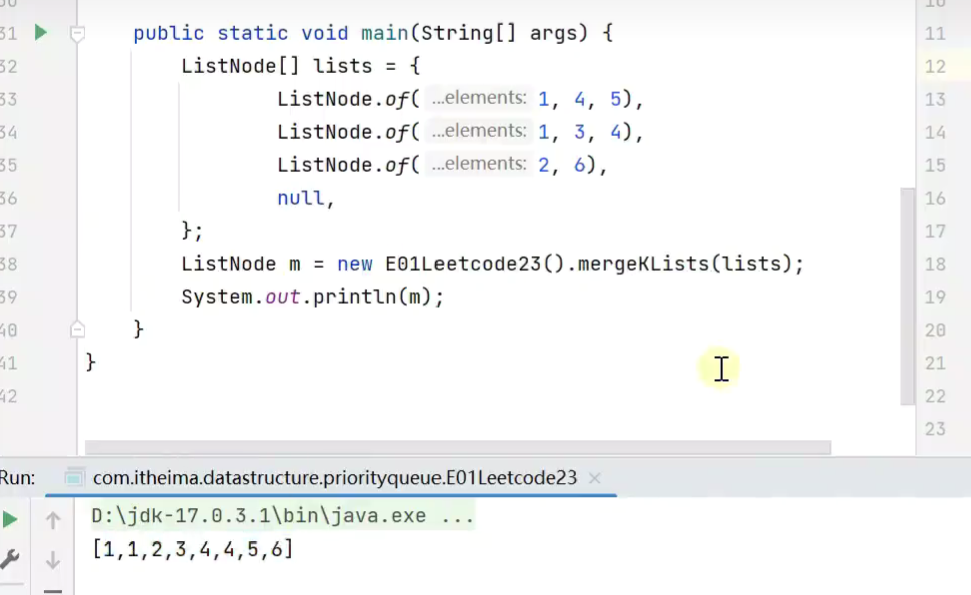
测试

效率低于分而治之

可以，但空间占用比上一种方式高

消费生产队列

上述队列存在的问题
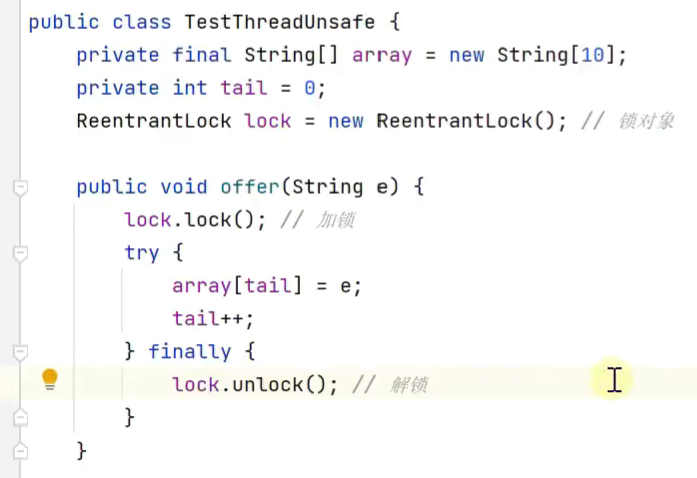
存在线程安全问题

运用锁保证线程安全

lockInterruptibly

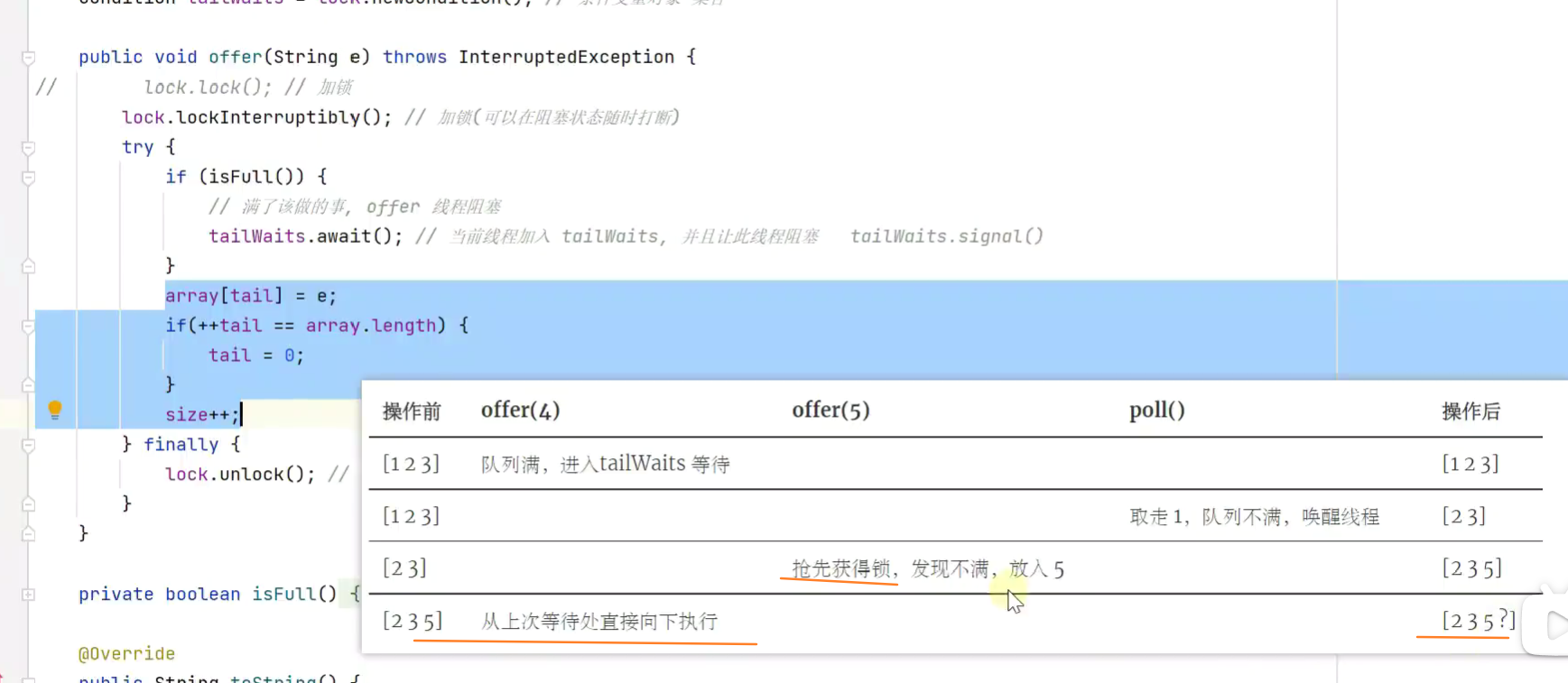
2.有缺陷的锁和唤醒

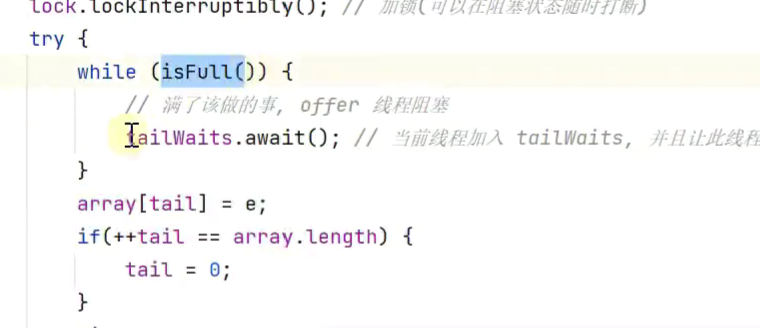
改进：将if改为while

while和if本身就用法不同，一个是循环语句，一个是判断语句。

if 就是一个判断的，如果满足后面的条件就继续运行if内部的语句，若不满足则跳出，执行else语句或执行下面的语句的。

while 就是循环语句的，当满足while里面的条件时，就会执行里面的循环体的，直到条件不满足为止。

双锁，入队和出队各自一把锁

运用原子整数类

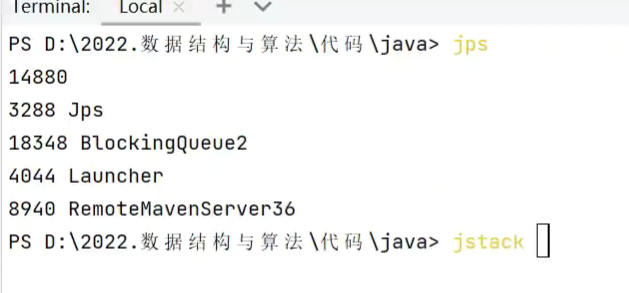
检查死锁的命令
jastack

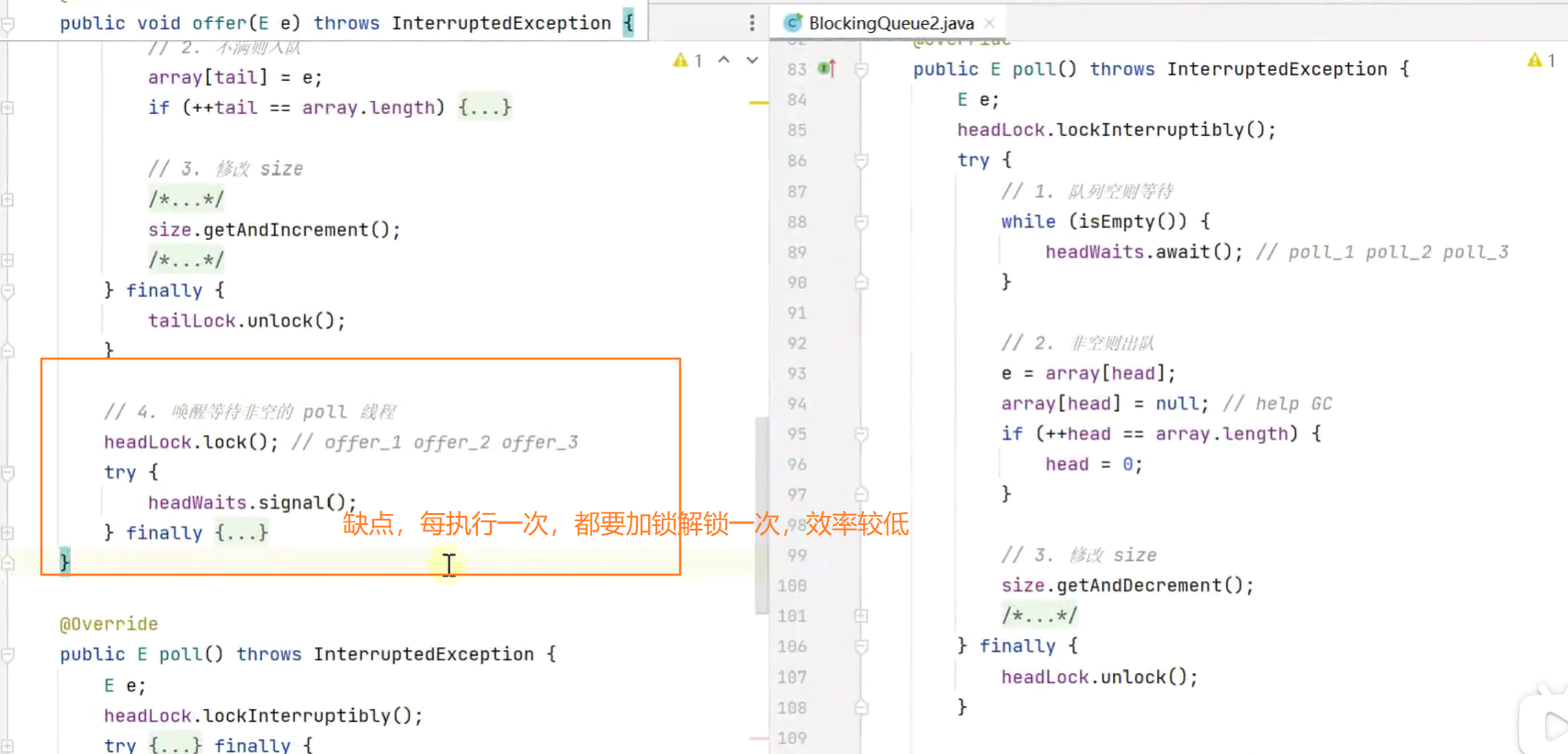
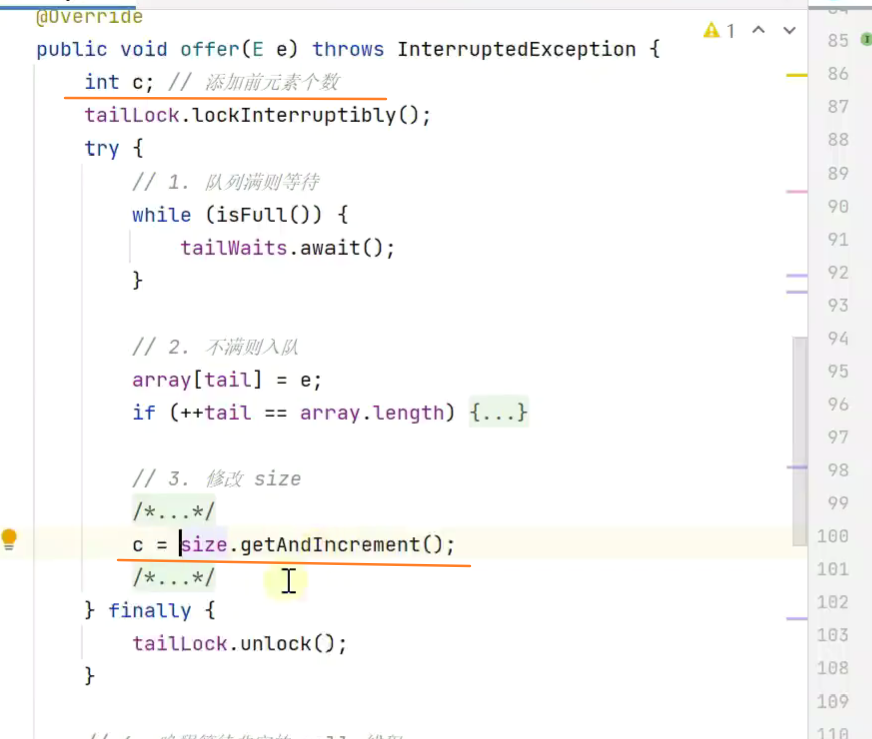
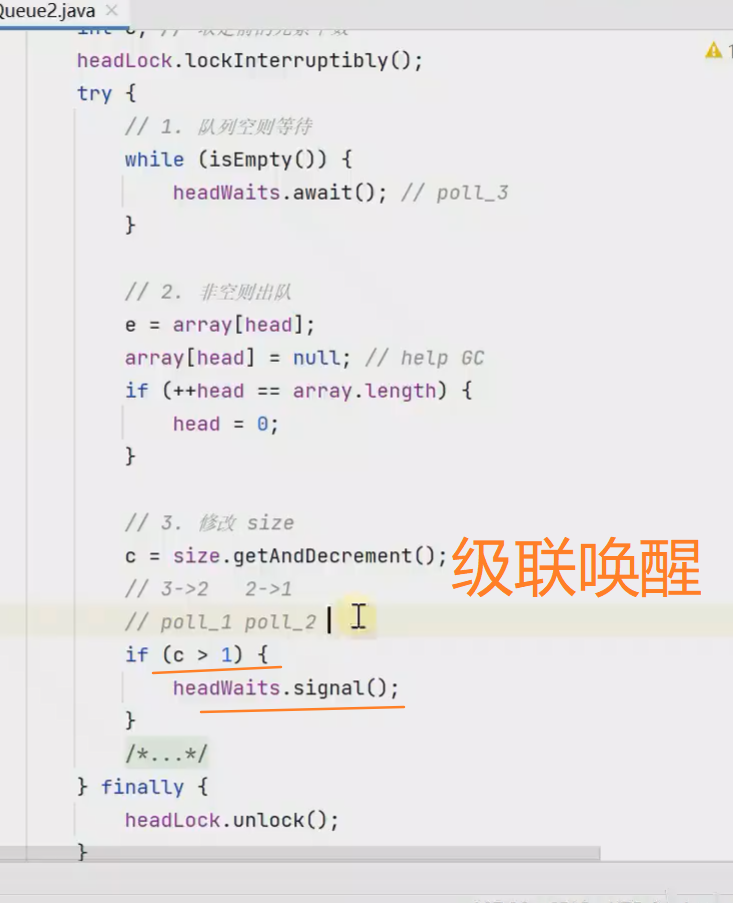
如何改进？

级联通知
减少加锁解锁的次数，只通知一个目标线程由该线程通知下一个线程

出队

入队类似
堆

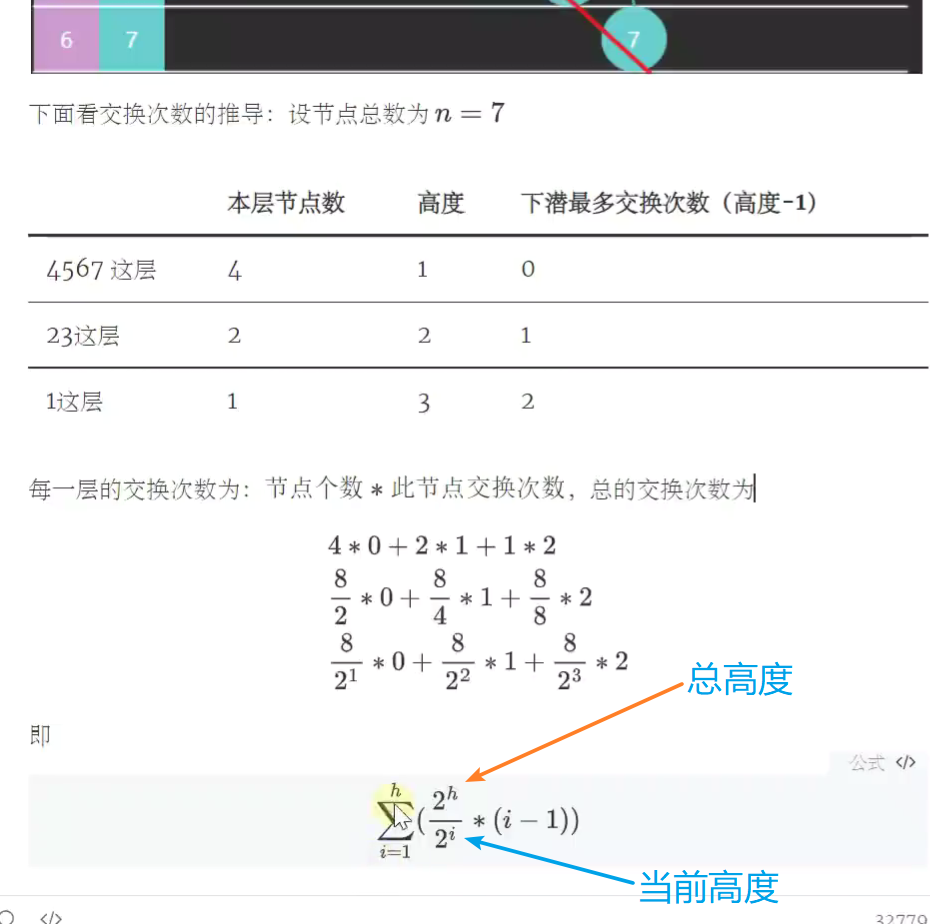
建堆

弗洛伊德建堆算法

具体实现

1.找到最后一个非叶子节点
size / 2 - 1(索引1为起点）

2.下潜

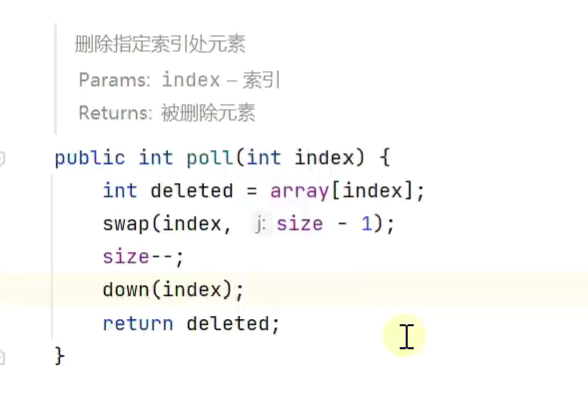
删除指定索引

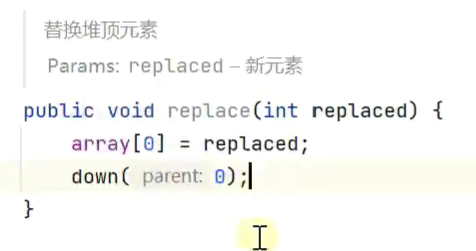
替换堆顶

上浮
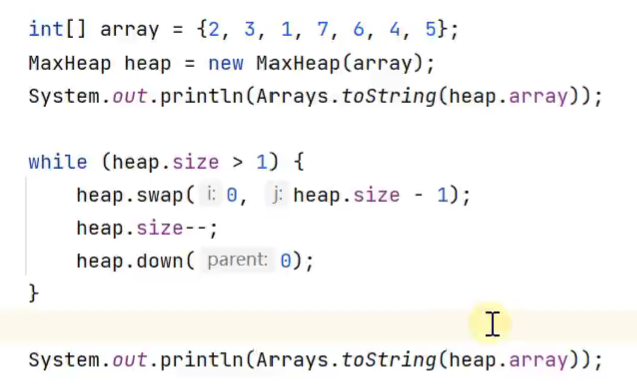
堆排序
不是O（N）,没有快速选择快
堆的应用

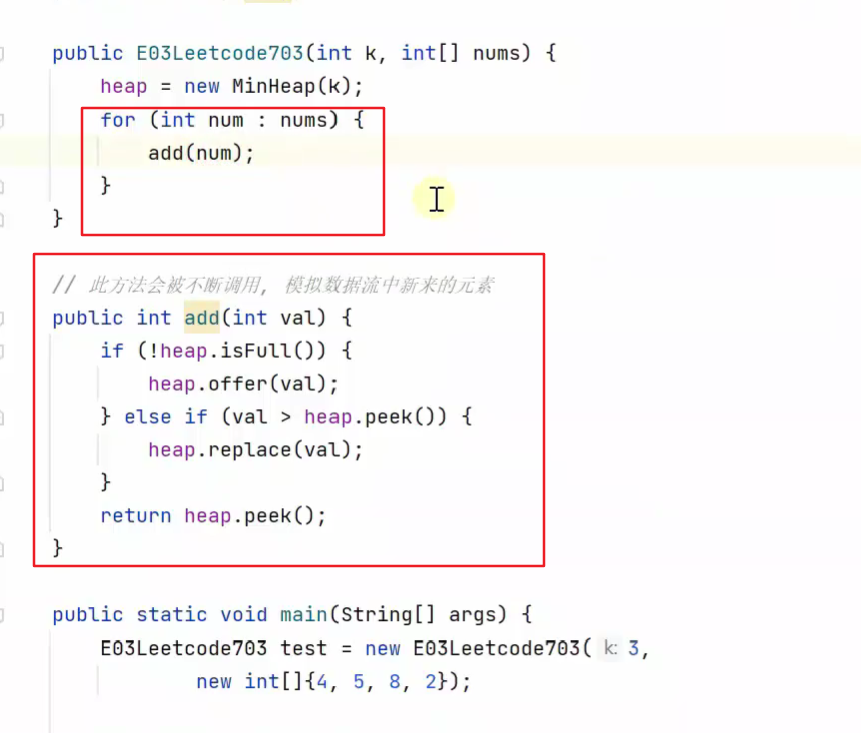
求数据流中第k大的元素
数据流：数据可变，可不断更新
适合用堆实现
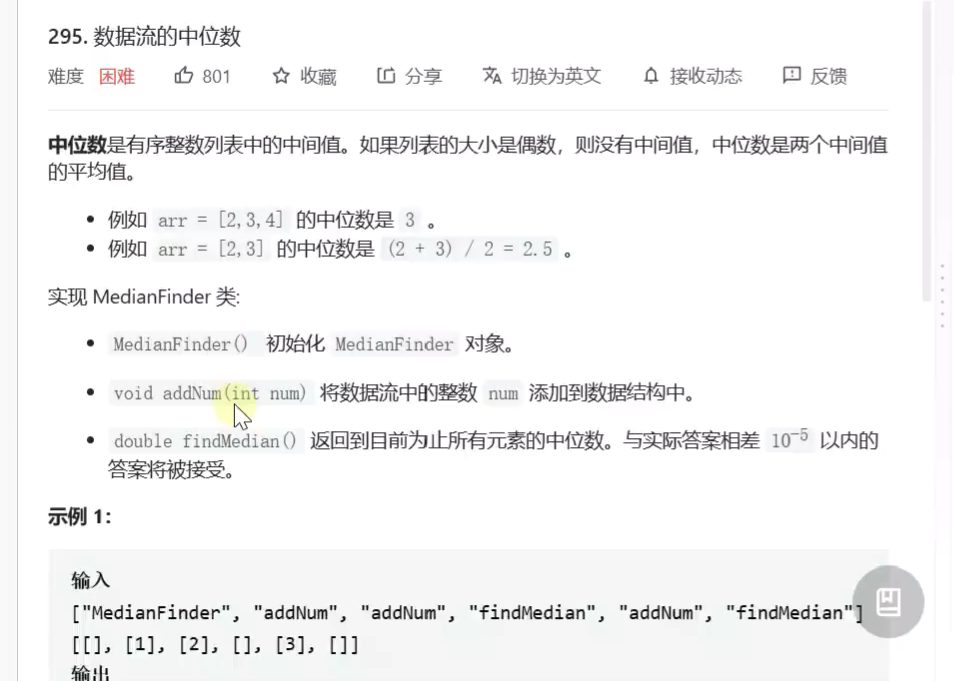
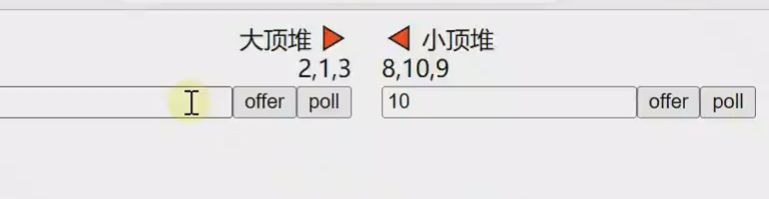
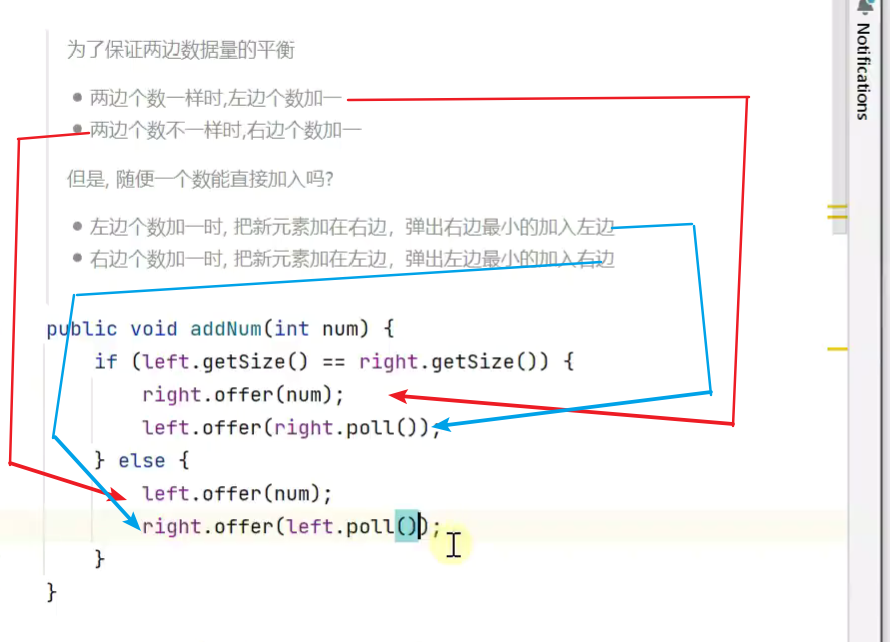
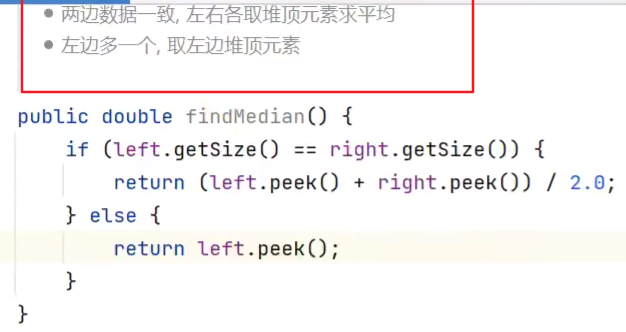
数据流中的中位数

因为右边最小的在左边是最大的

3

利用Java自带的优先队列实现
PriorityQueue默认小顶堆0
可通过传入比较器作为参数构造大顶堆·
二叉树

使用递归实现前、中、后序遍历

前序遍历

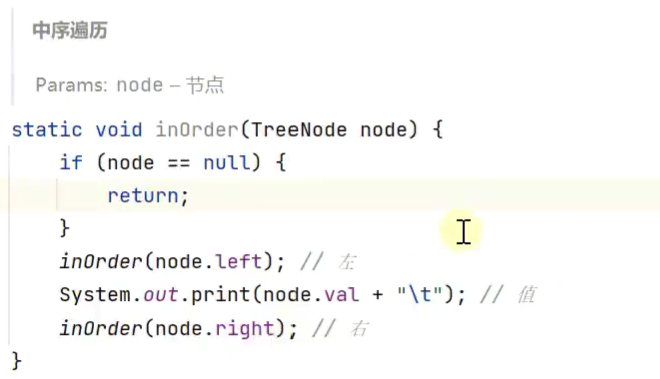
中序遍历

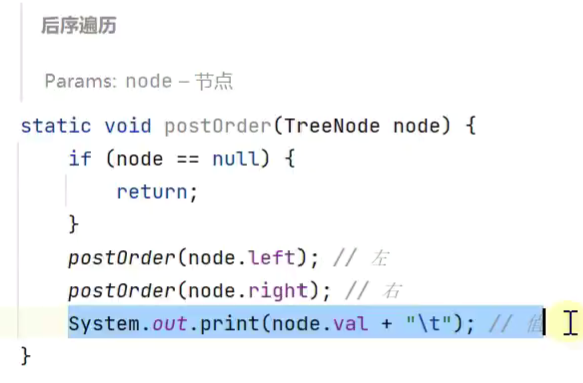
后序遍历

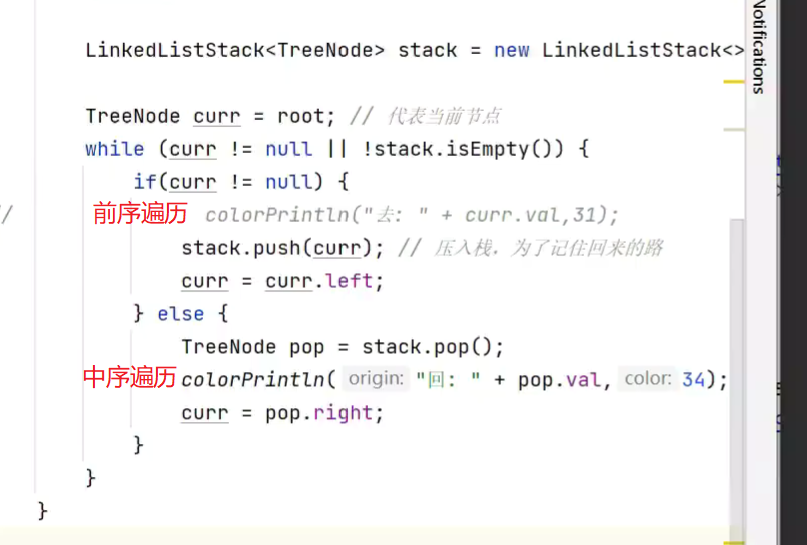
非递归实现

走的路径是一样的
利用栈记录来时走过的路径

分别实现前序和中序遍历

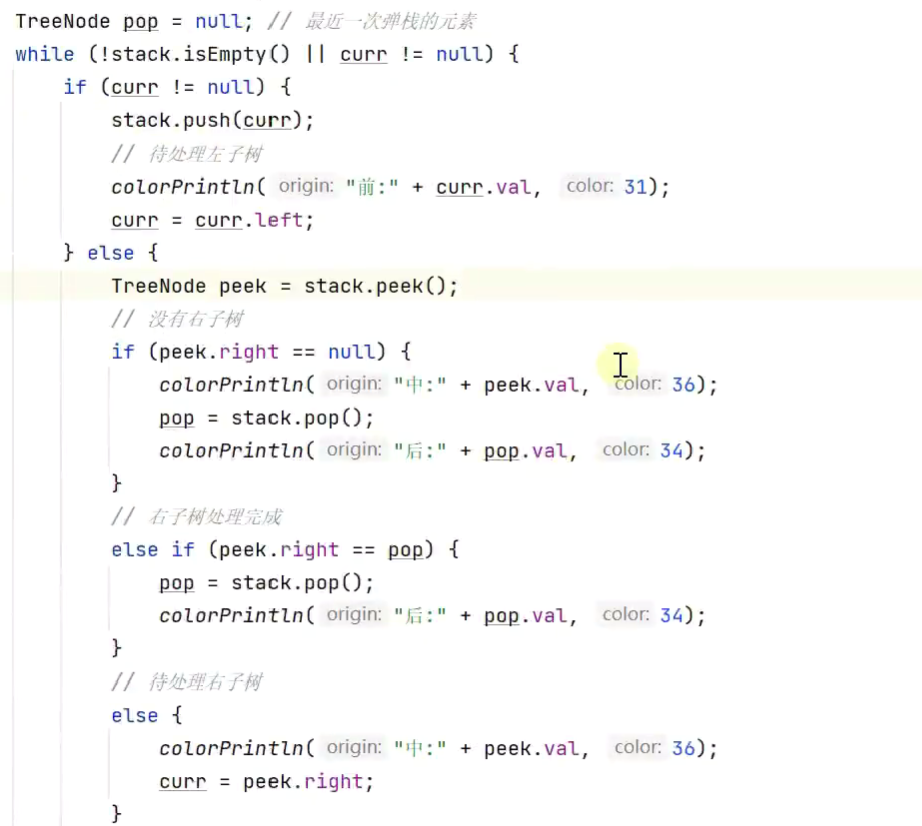
后序遍历

前中后序整合版
检验二叉树是否对称
二叉树最大深度

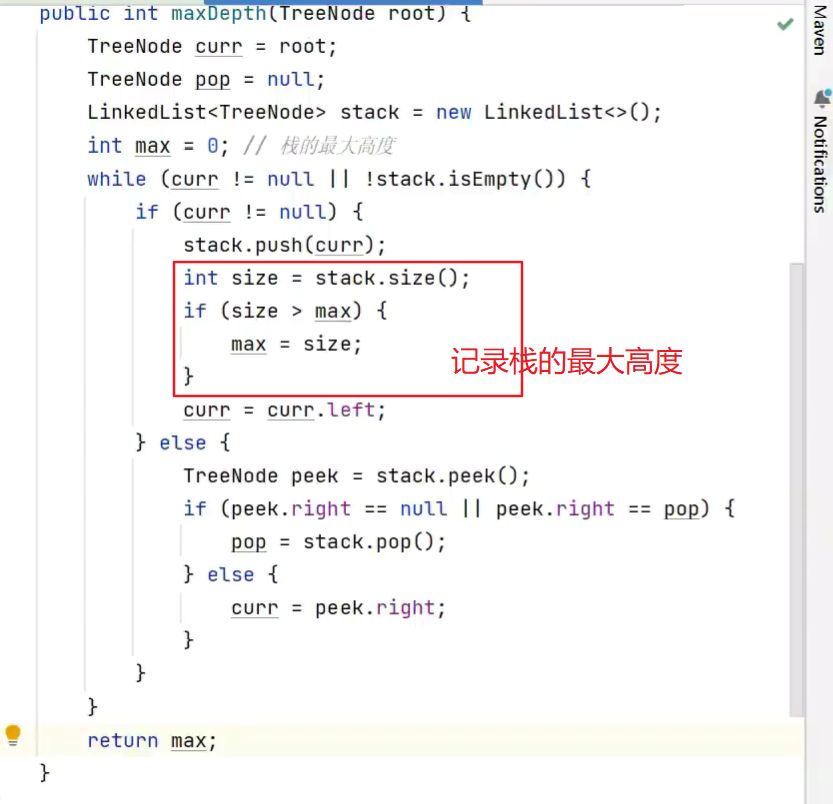
2。不是用递归，使用后序遍历
栈的最大高度即为二叉树最大深度

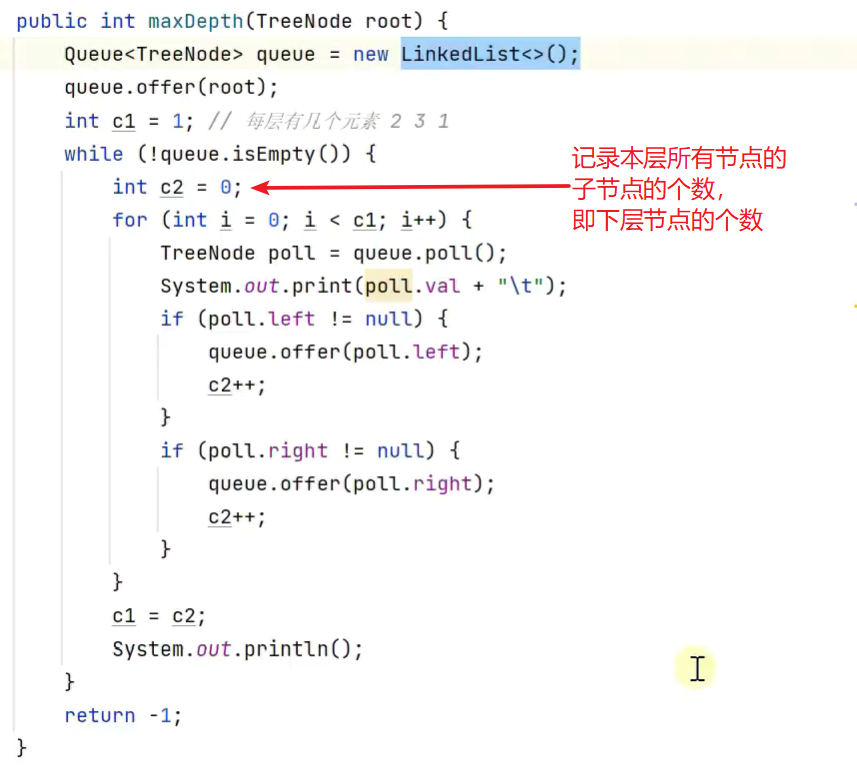
3.使用层序遍历
效率更高

层数即为最大深度

简化
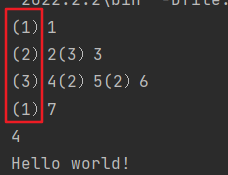
szie为队列元素个数，也为一层的元素个数，因为上一层已经poll出去

若将 i < size 改为i < queue.size() ,择遍历输出结果不正确

因为再次进入if判断时，queue.size()会被更新成现在队列中的元素个数，即为输出的层的下一层的元素个数，而size不会被更新，只有退出if判断（输出当前层节点）后，重新进入while循环，执行到size = queue.size()时被更新为队列中现有的元素个数，即需要打印在控制台的层的元素个数
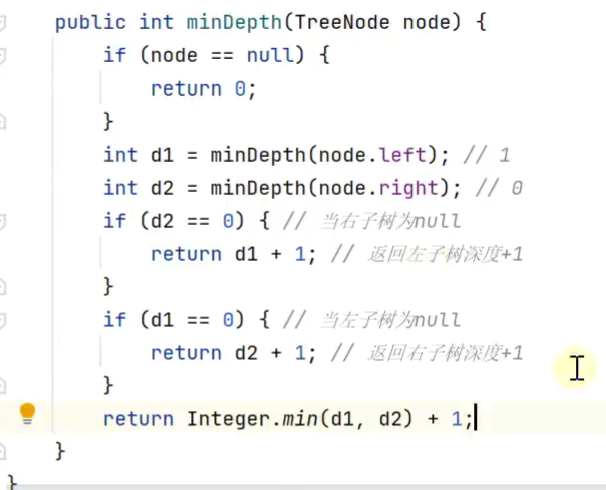
二叉树最小深度

1.递归

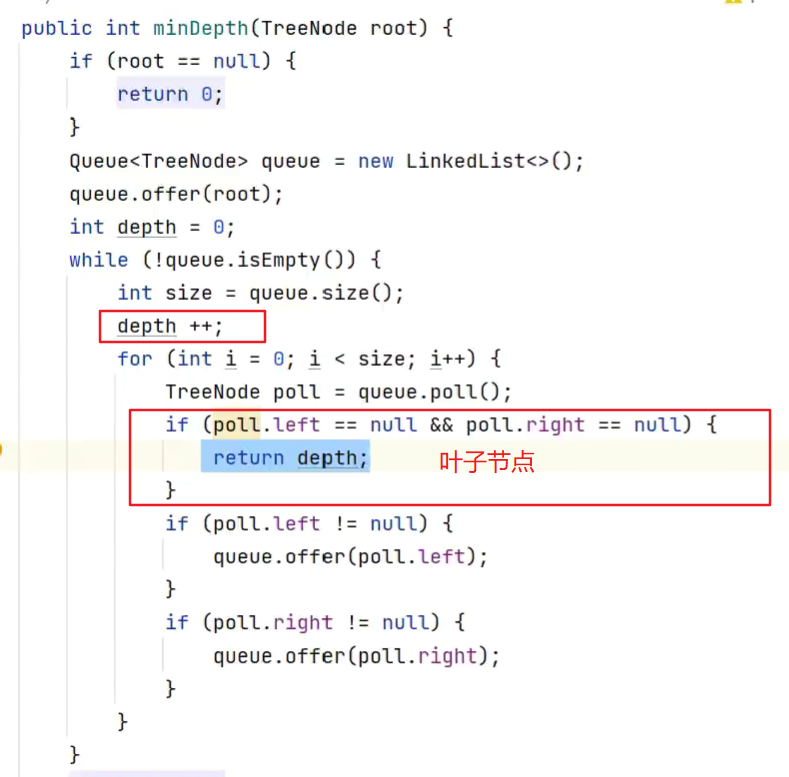
2.层序遍历
遇到的第一个叶子节点所在层就是最小深度
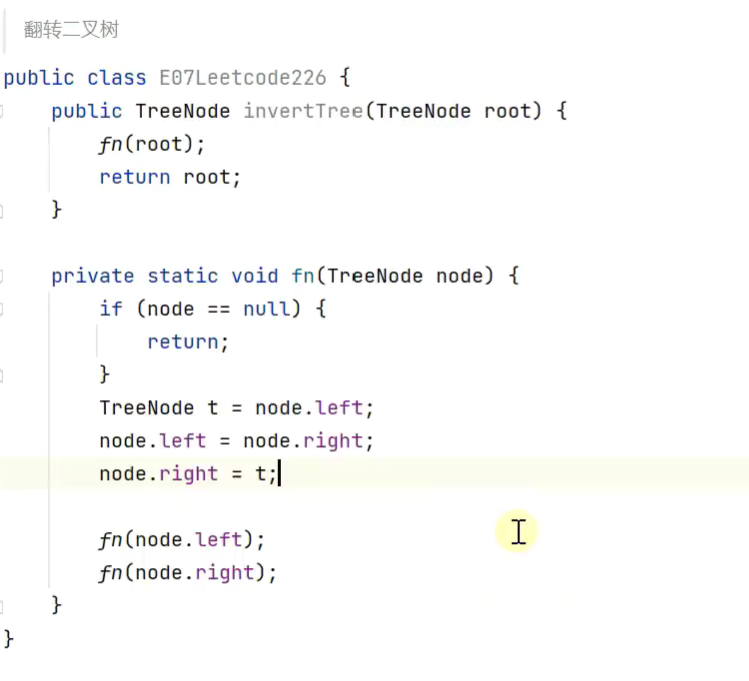
翻转二叉树

递归
交换
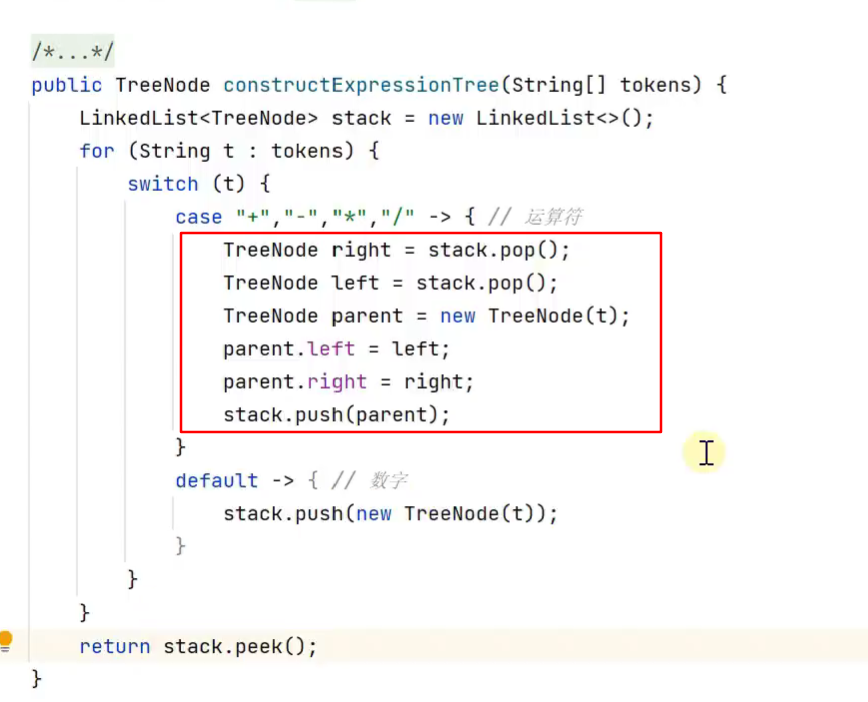
后缀表达式写为二叉树

思路
根据前序中序遍历结果构造二叉树
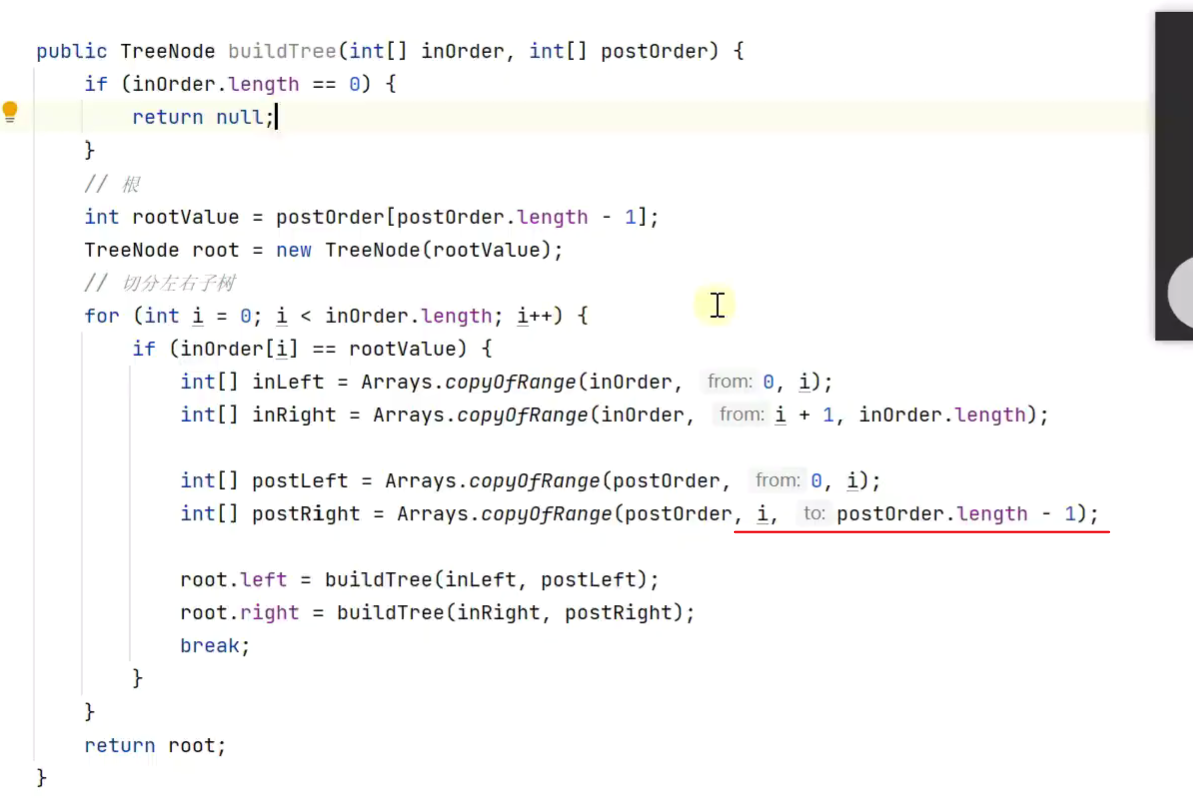
根据中后遍历结果还原二叉树

、

二叉搜索树

查找
递归

非递归

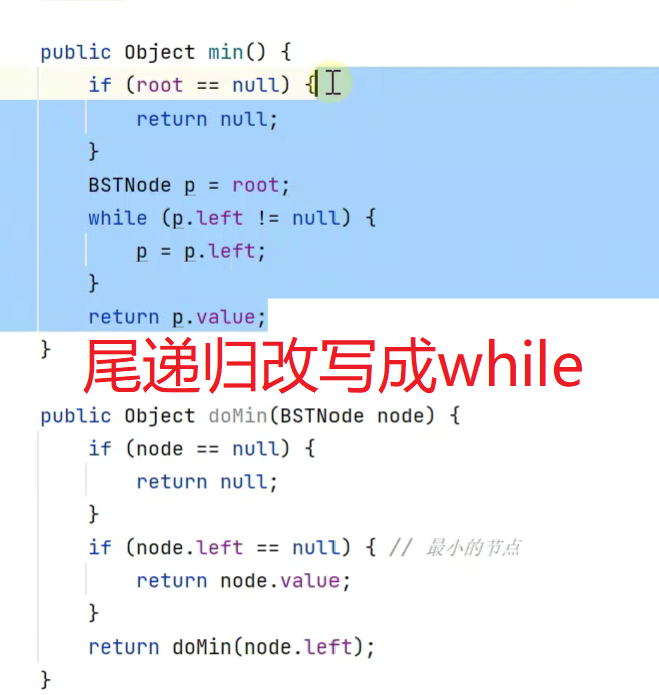
尾递归一般很容易转换成循环，即 return只调用自身
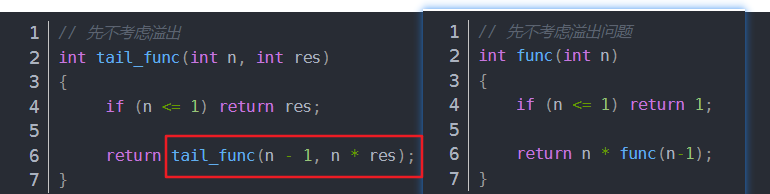
例：

在上面写的一般递归函数 func() 中，我们可以看到，
func(n) 是依赖于 func(n-1) 的，func(n) 只有在得到 func(n-1) 的结果之后，才能计算它自己的返回值，
因此理论上，在 func(n-1) 返回之前，func(n)，不能结束返回。因此func(n)就必须保留它在栈上的数据，直到func(n-1)先返回，而尾递归的实现则可以在编译器的帮助下，消除这个限制：

从上可以看到尾递归把返回结果放到了调用的参数里。这个细小的变化导致，
tail_func(n, res)不必像以前一样，非要等到拿到了tail_func(n-1, nres)的返回值，才能计算它自己的返回结果 – 它完全就等于tail_func(n-1, nres)的返回值。
因此理论上：tail_func(n)在调用tail_func(n-1)前，完全就可以先销毁自己放在栈上的东西。

这就是为什么尾递归如果在得到编译器的帮助下，是完全可以避免爆栈的原因：
每一个函数在调用下一个函数之前，都能做到先把当前自己占用的栈给先释放了，尾递归的调用链上可以做到只有一个函数在使用栈，因此可以无限地调用！

Java不支持尾递归自动优化，所以最好自己改写成循环

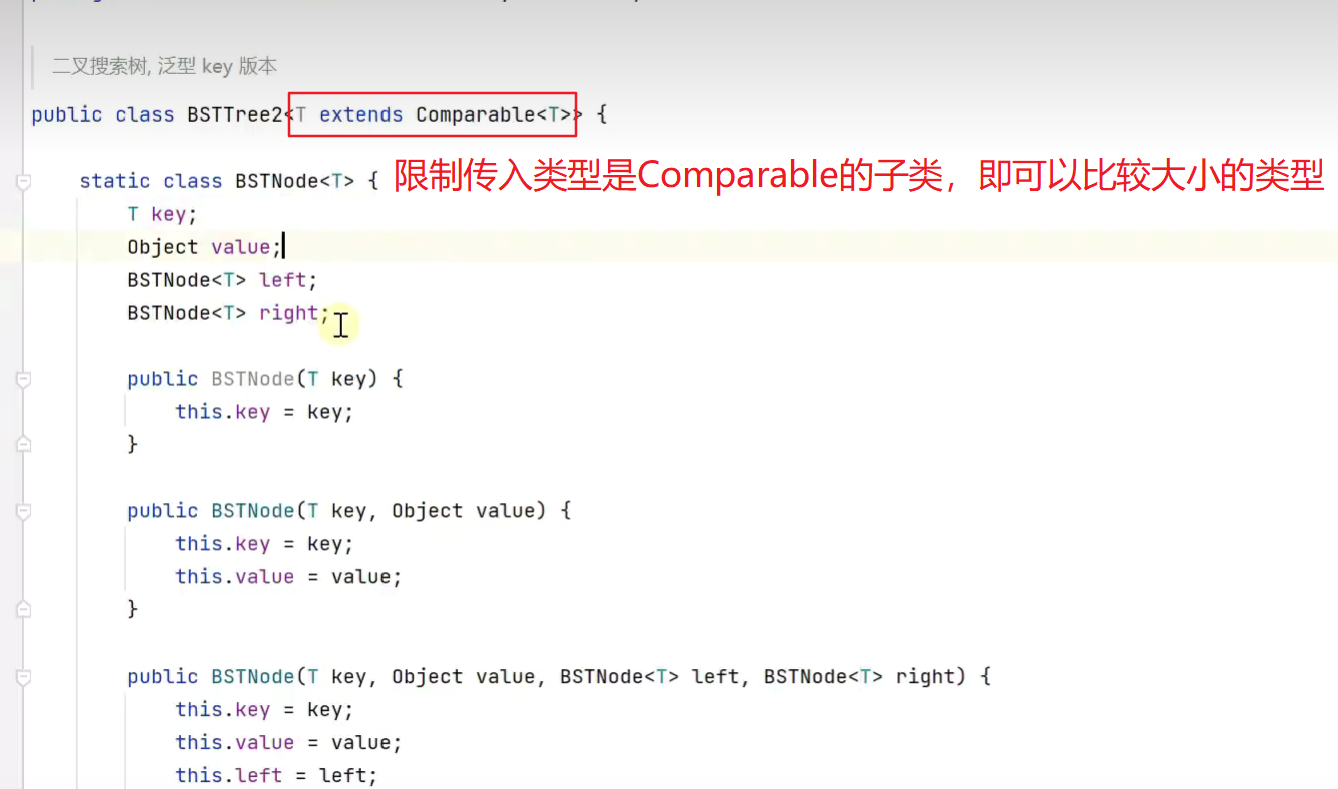
二叉搜索树，泛型版本.

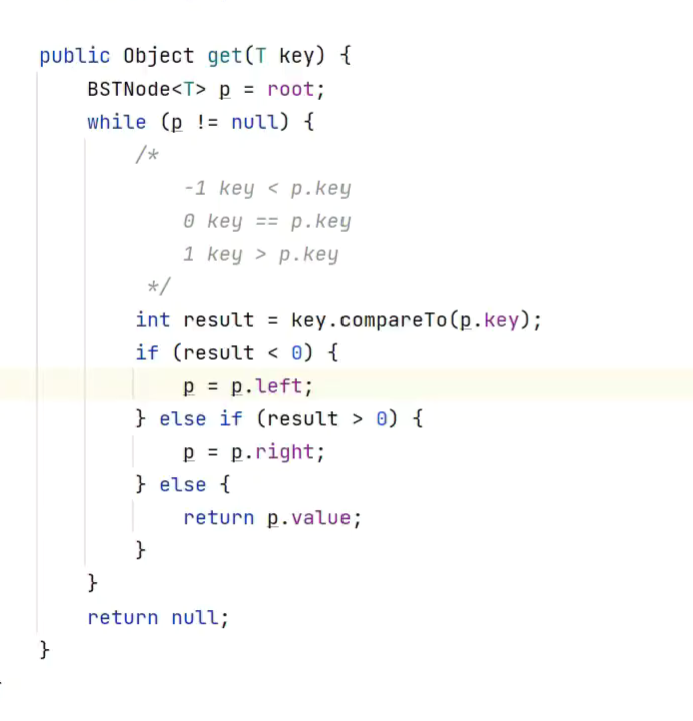
get

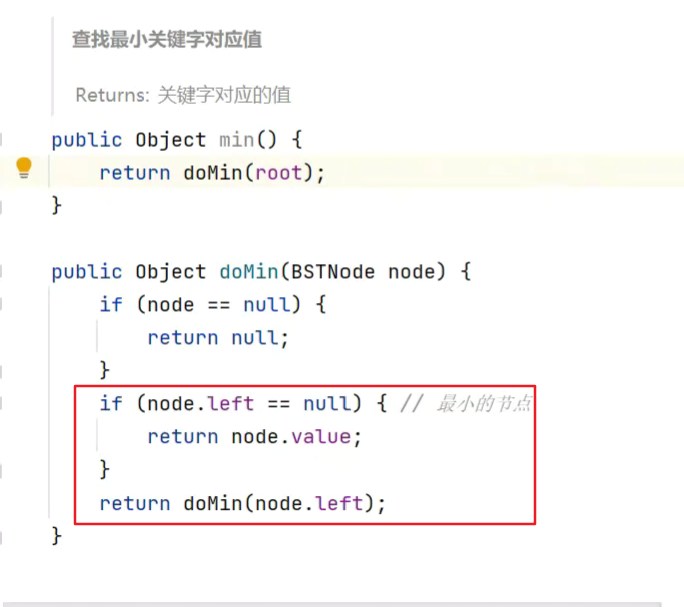
查找最小
1.递归

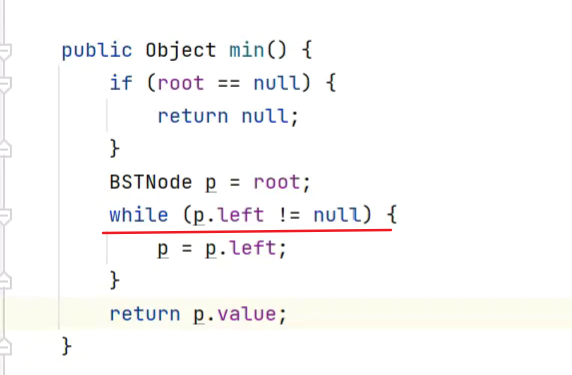
2.非递归
用while

查找最大

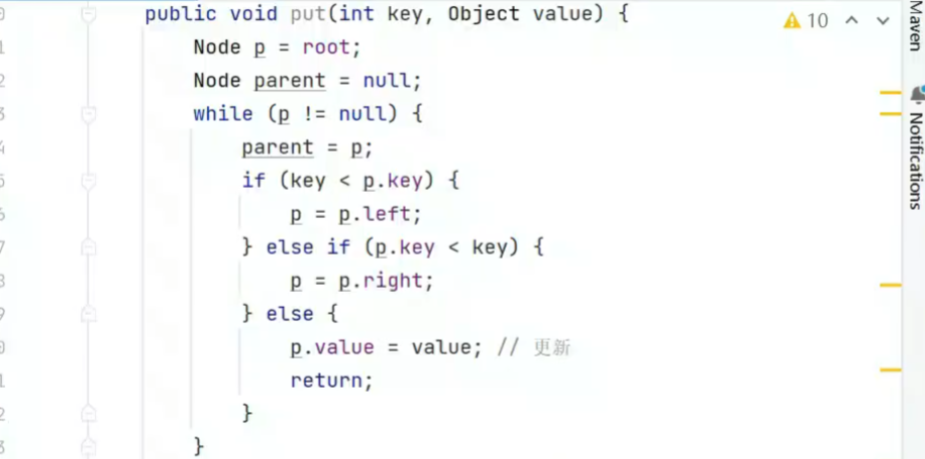
put类似map的put

删除节点

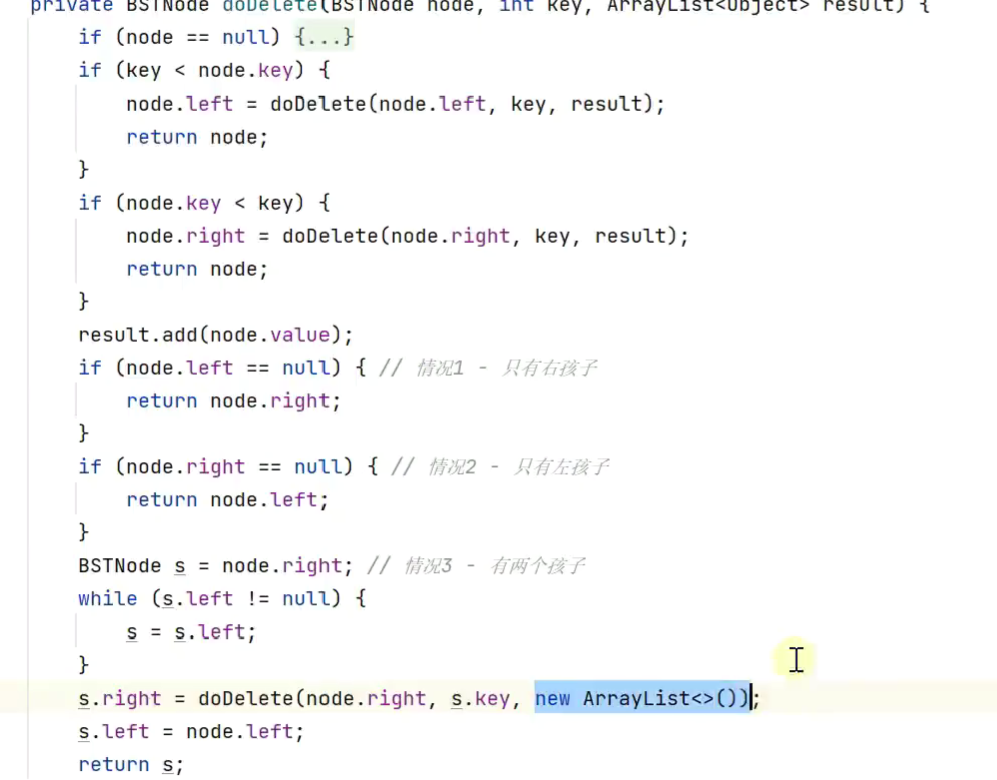
递归删除
寻找小于key的所有节点

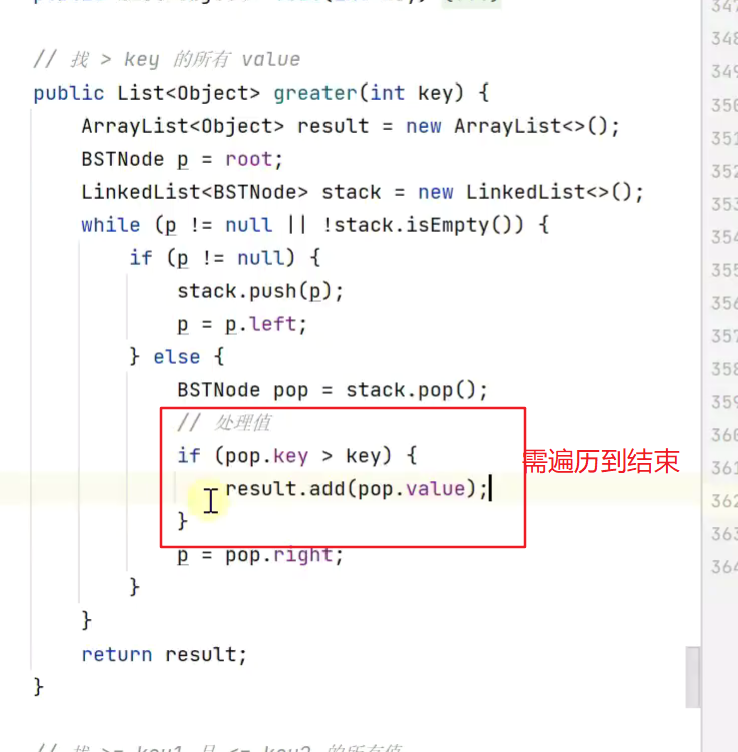
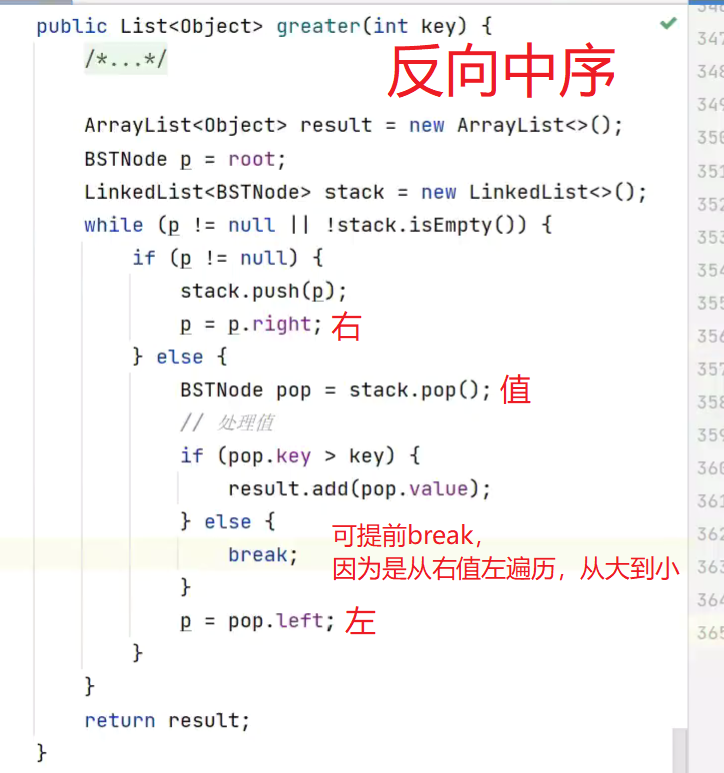
寻找大于key的所有值
从头到尾遍历一遍

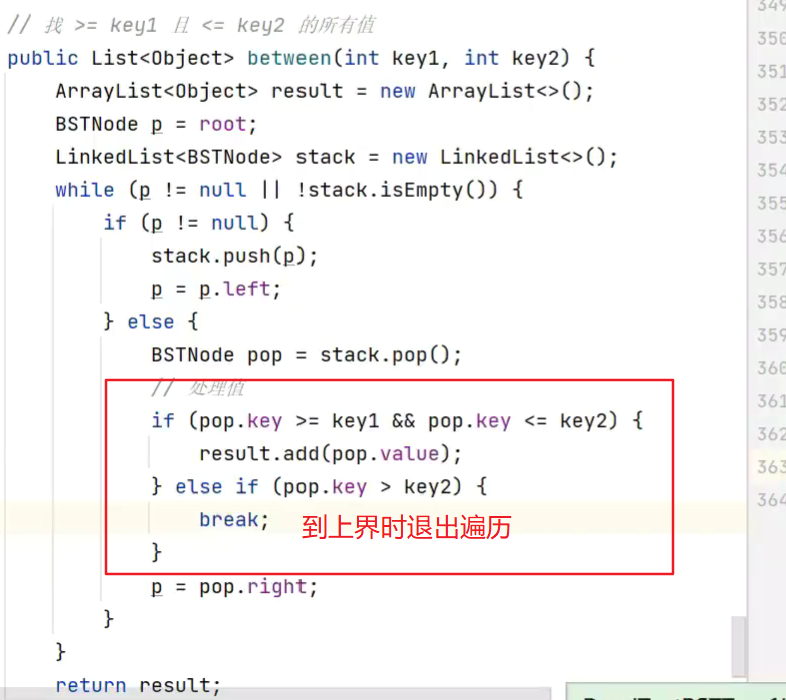
寻找 key1 和key2之间的所有元素

缺点，寻找大于key时，不能提早结束循环，，可用反向中序遍历优化
二叉搜索树
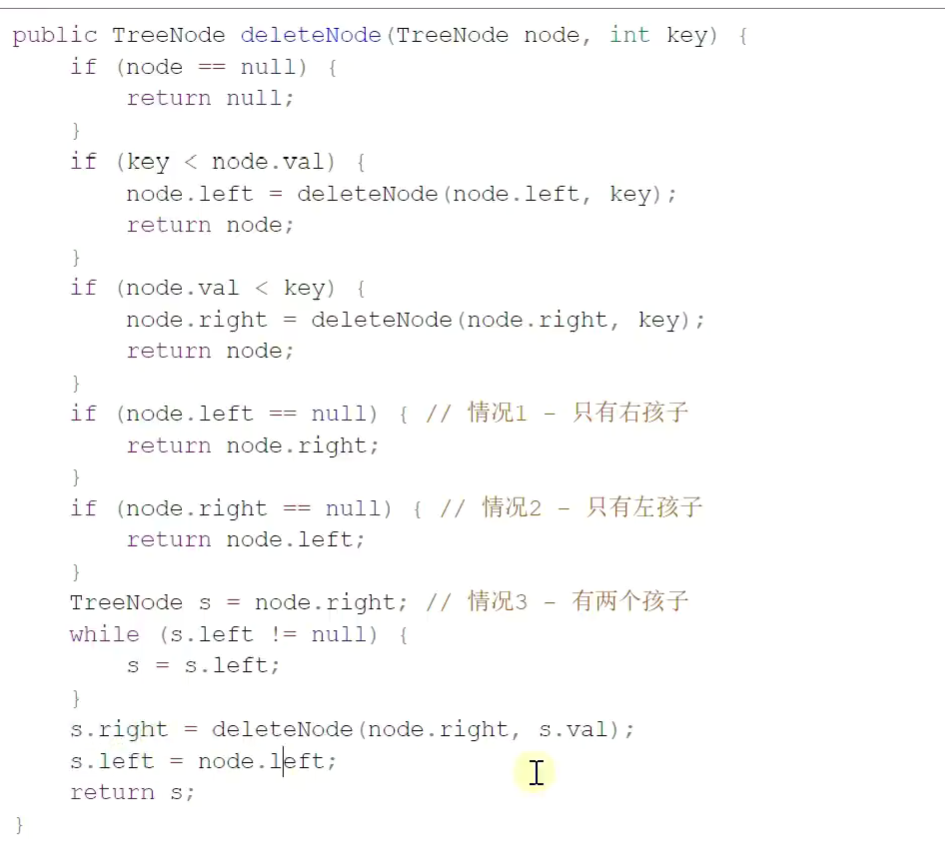
1.删除节点

2.新增节点

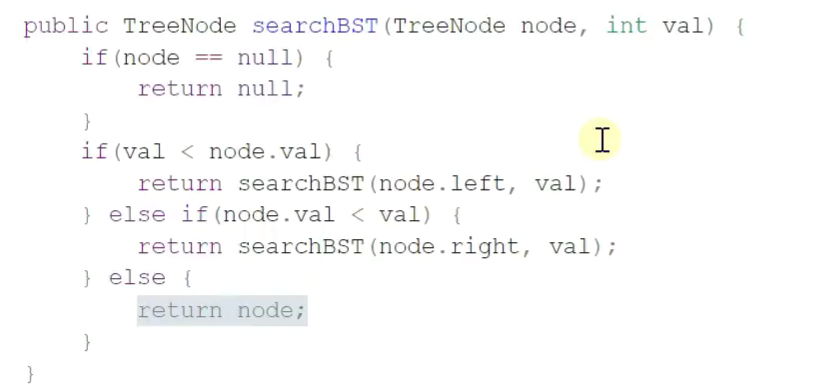
3.查询

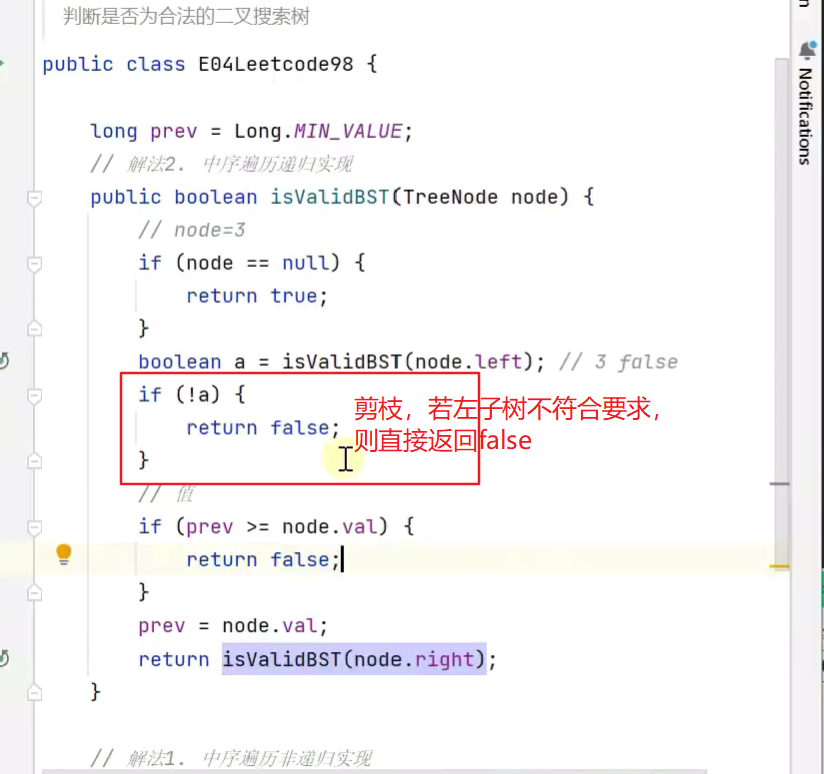
4.验证是否为合法二叉搜索树

非递归

递归（初版）

进阶版，剪枝，去除多余的递归操作

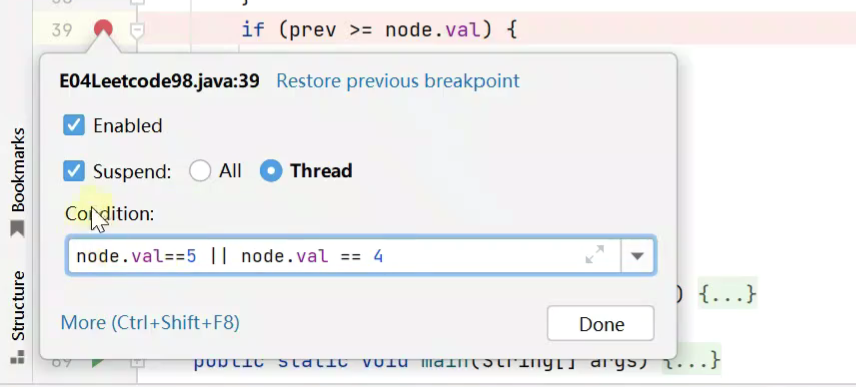
3.将prev 作为函数传入

debug自定义断点停止的条件

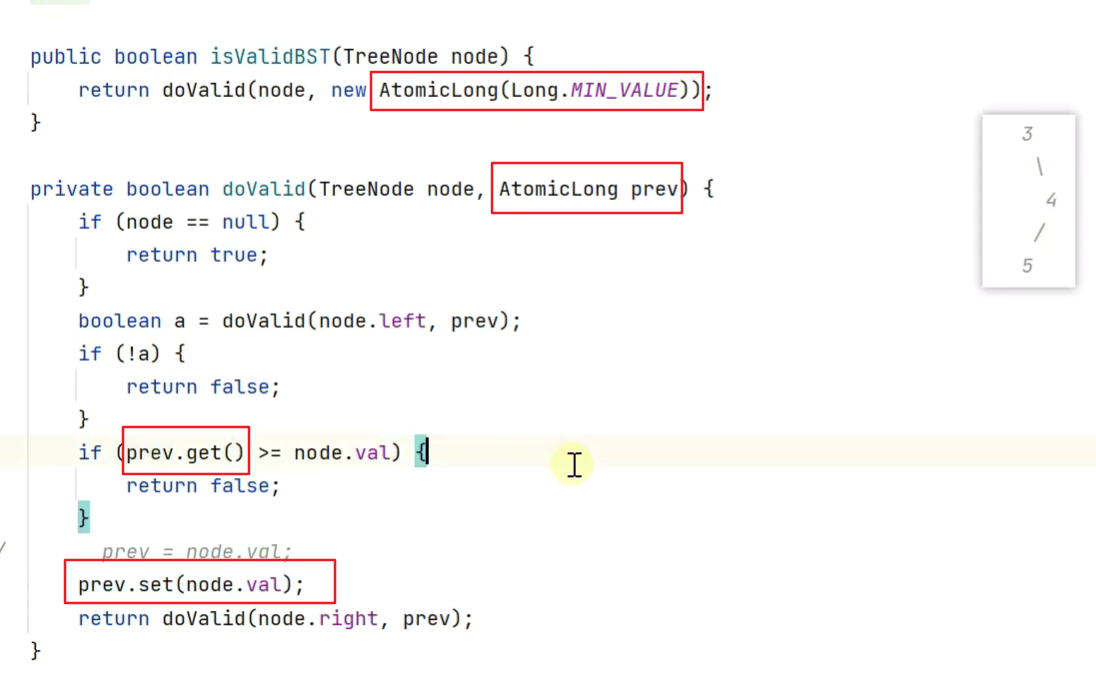
改进，改为传入一个对象

4.上下限判断是否是二叉搜索树
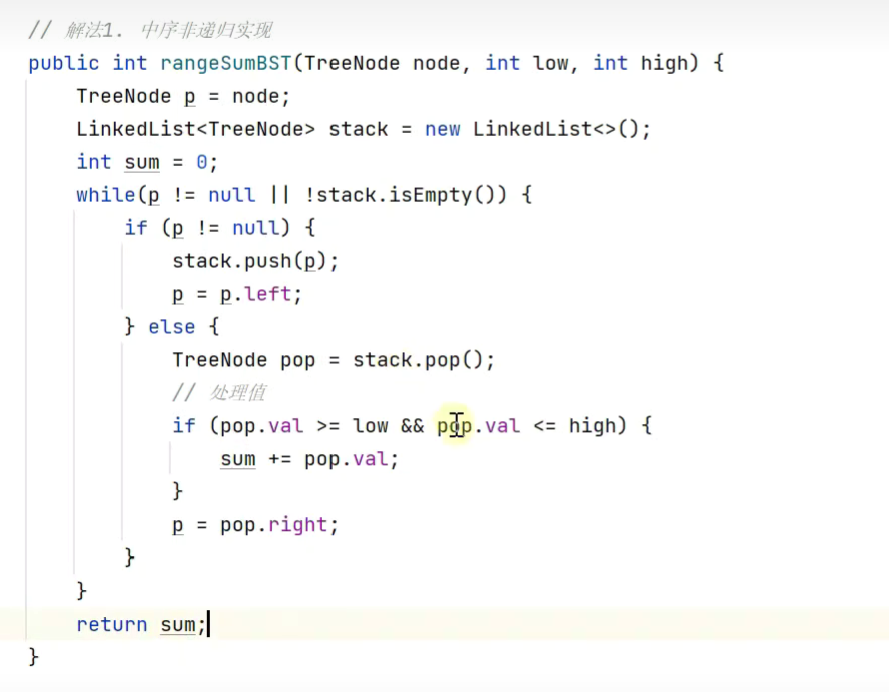
二叉搜索树范围内求和

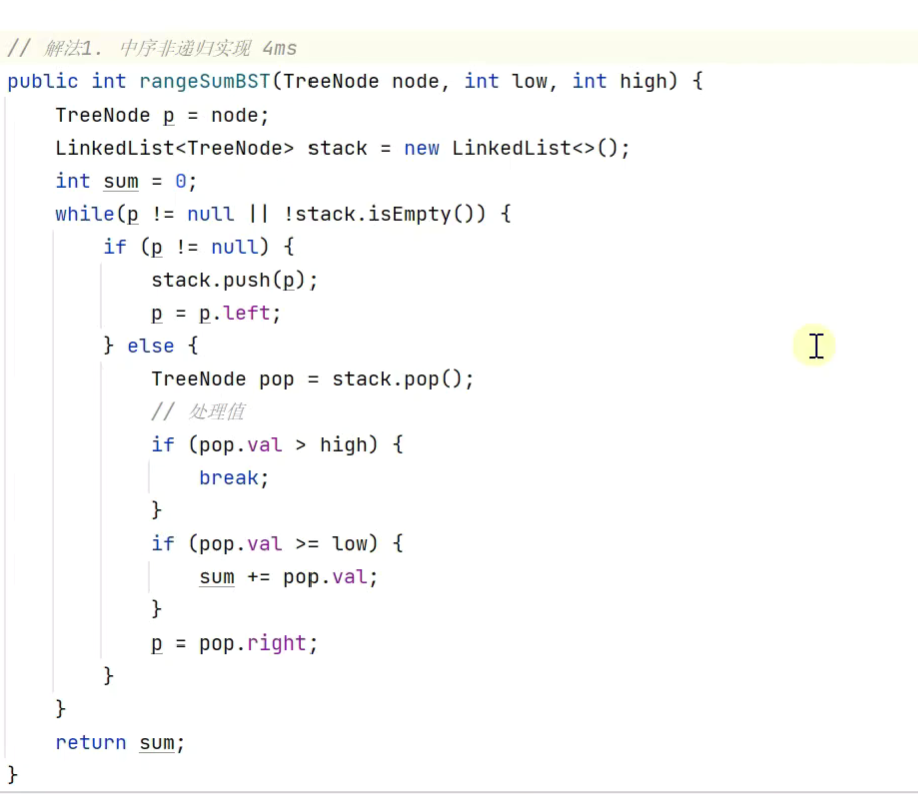
改版，提前结束遍历，减少不必要的遍历

缺点,速度较慢，性能不高。

3.Pro 上下限递归
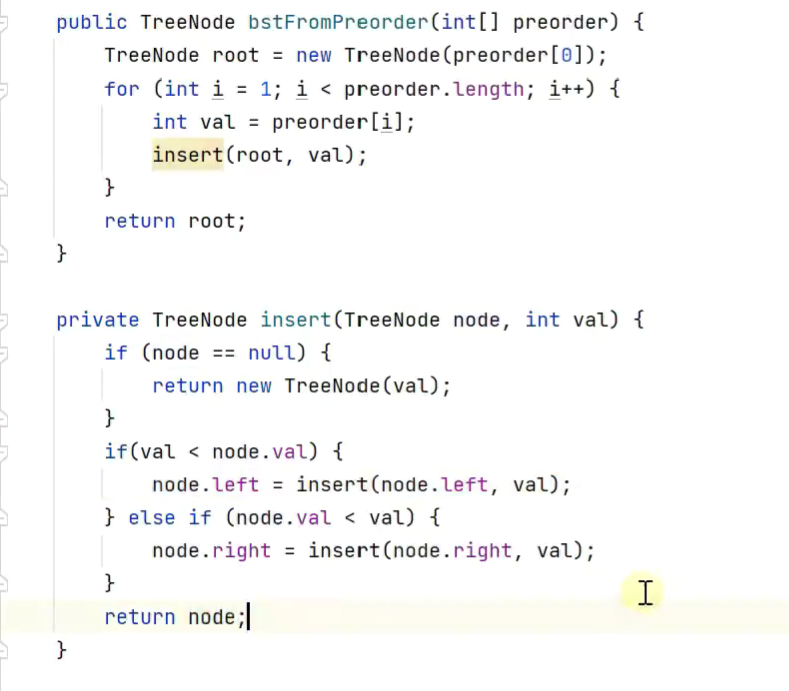
根据前序遍历构造二叉搜索树

1.时间复杂度 nlogn

2.上限法

时间复杂度O（n)

3.分治法
逐步切割根和左右子树
nlogn
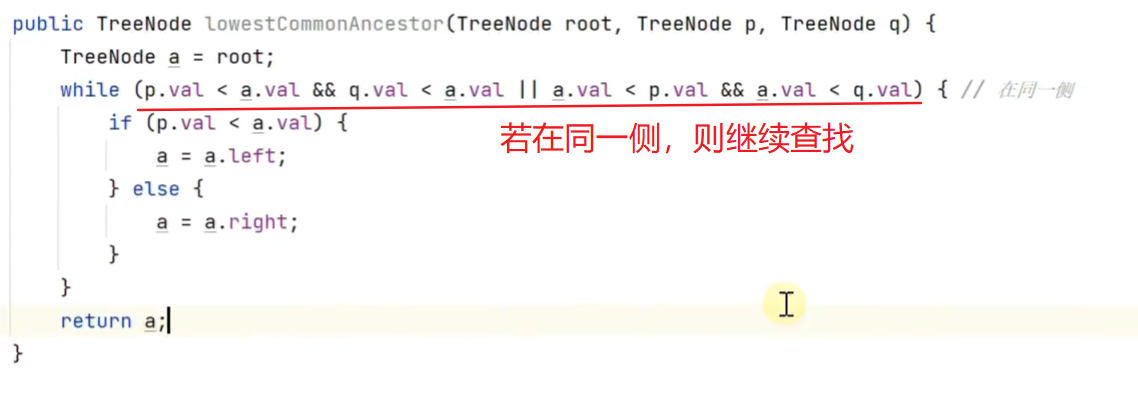
求二叉搜索树最近公共祖先

待查找节点 p q 在某一节点的两侧，那么此节点就是最近的公共祖先
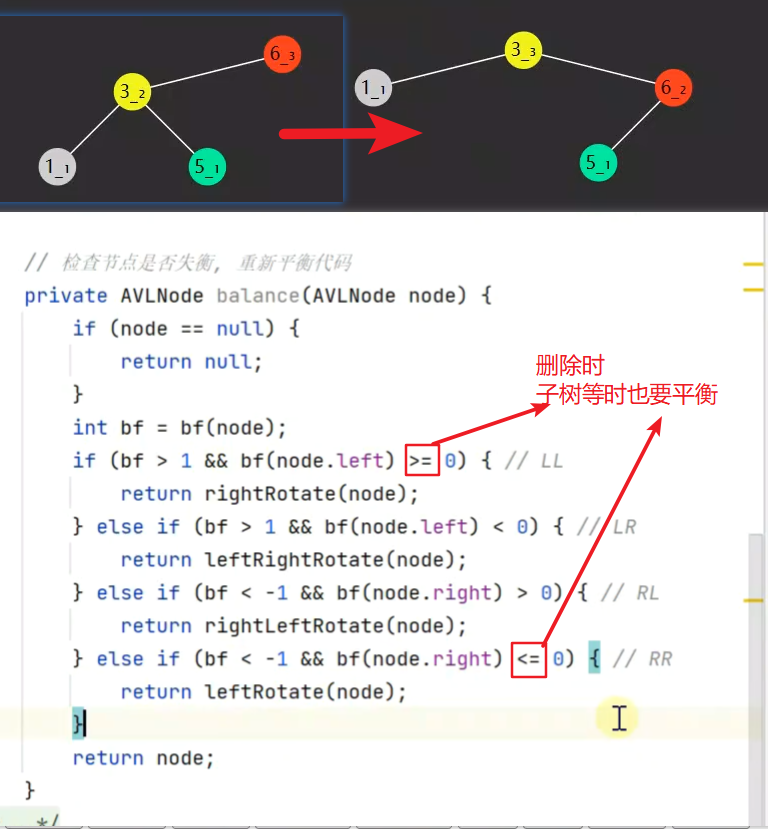
avl树自平衡二叉搜索树

如果一个节点的左右孩子，噶偶调查超1，则此节点失衡，才需要旋转

四种失衡情况
LL LR RL RR

LL和RR可分别通过一次右旋一次、一次左旋恢复平衡
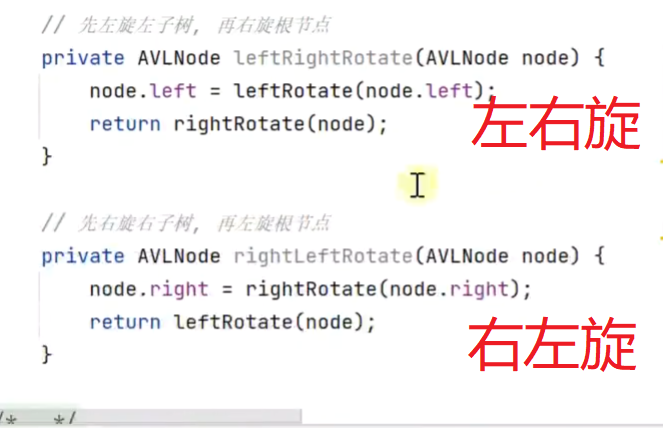
LR 先左旋再向右旋
RL 先右旋再向左旋

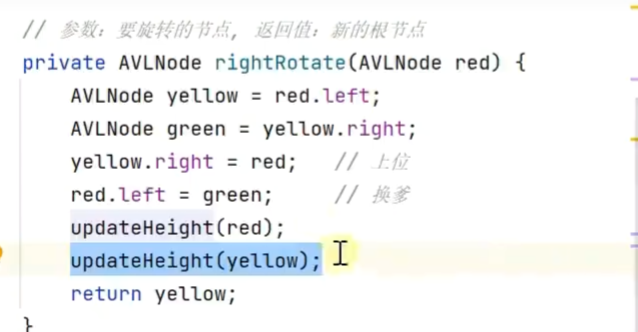
右旋

左旋类似

更新高度

顺序不能交换，先更新较低位置的高度

新增及更新

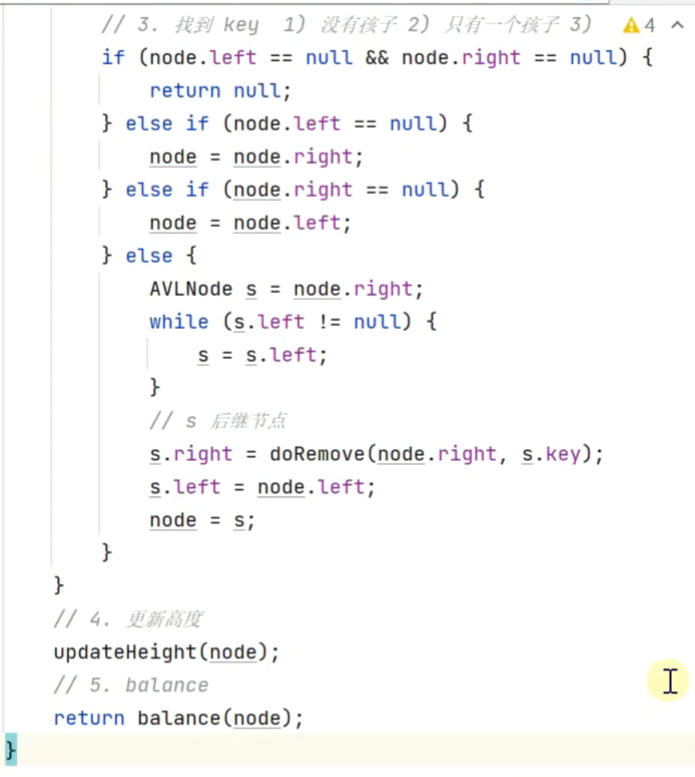
删除
红黑树
自平衡的二叉搜索树

一般黑色叶子节点成对出现或只有红色叶子节点才有可能达到平衡

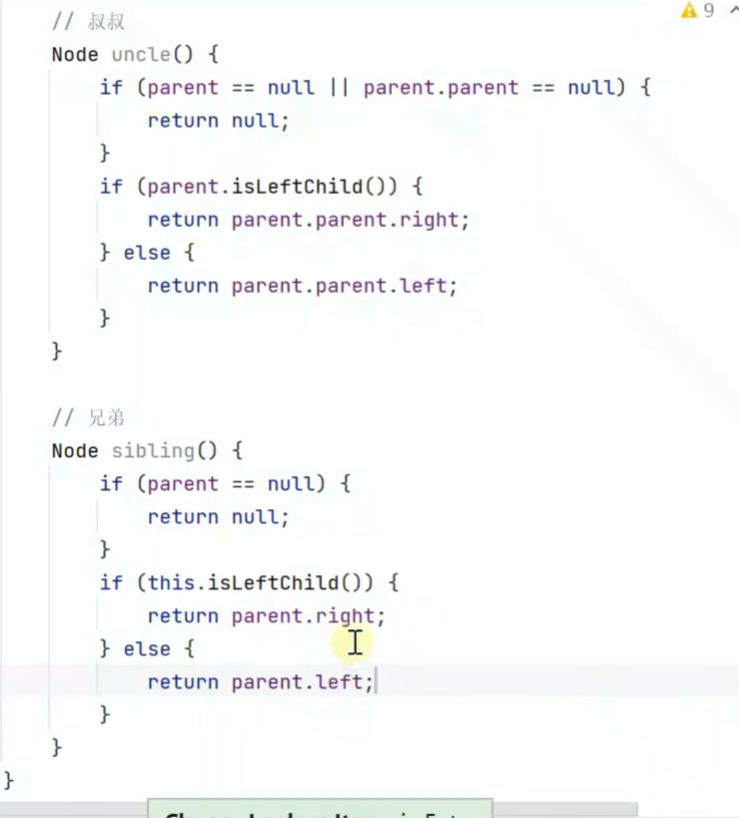
返回叔叔和兄弟节点

判断颜色

右旋、左旋（左旋同理）

插入和删除

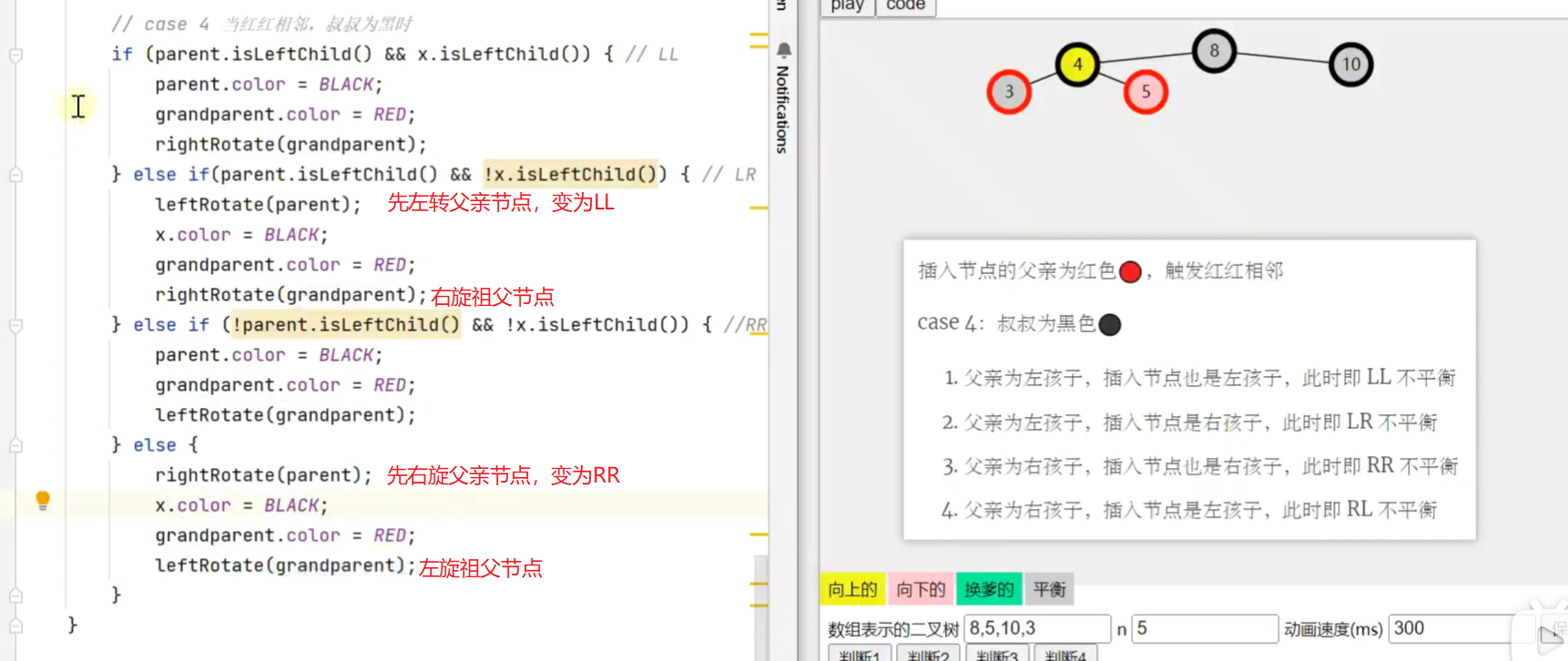
红红相邻处理



去除多于代码

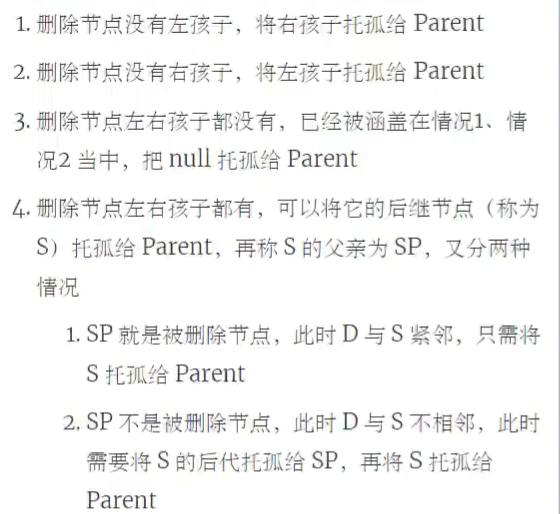
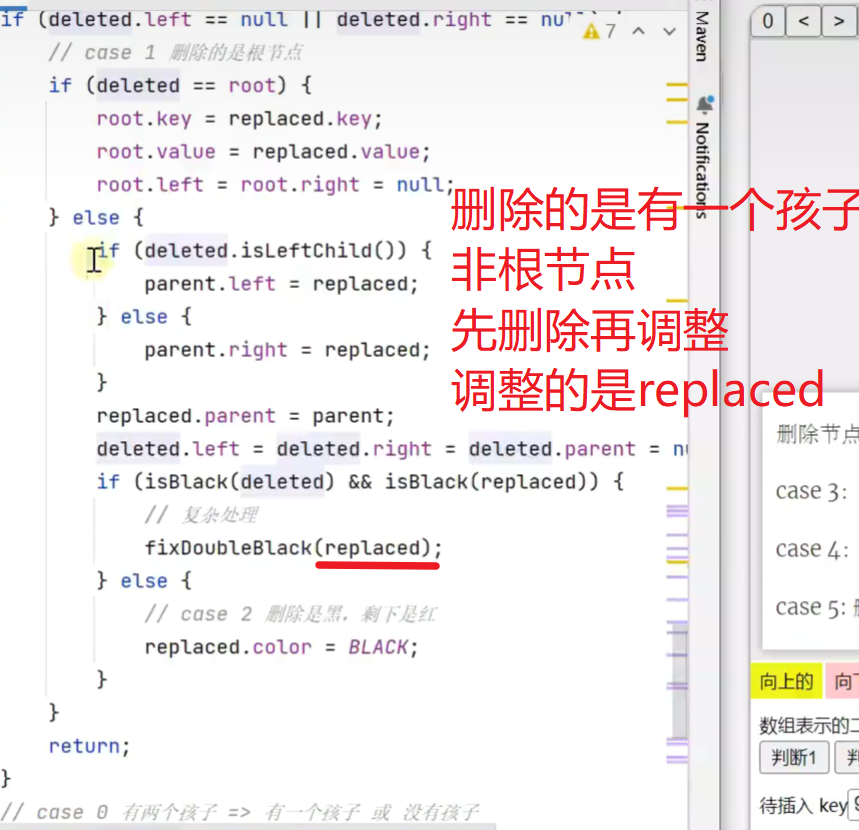
删除节点

查找删除节点

查找剩余节点

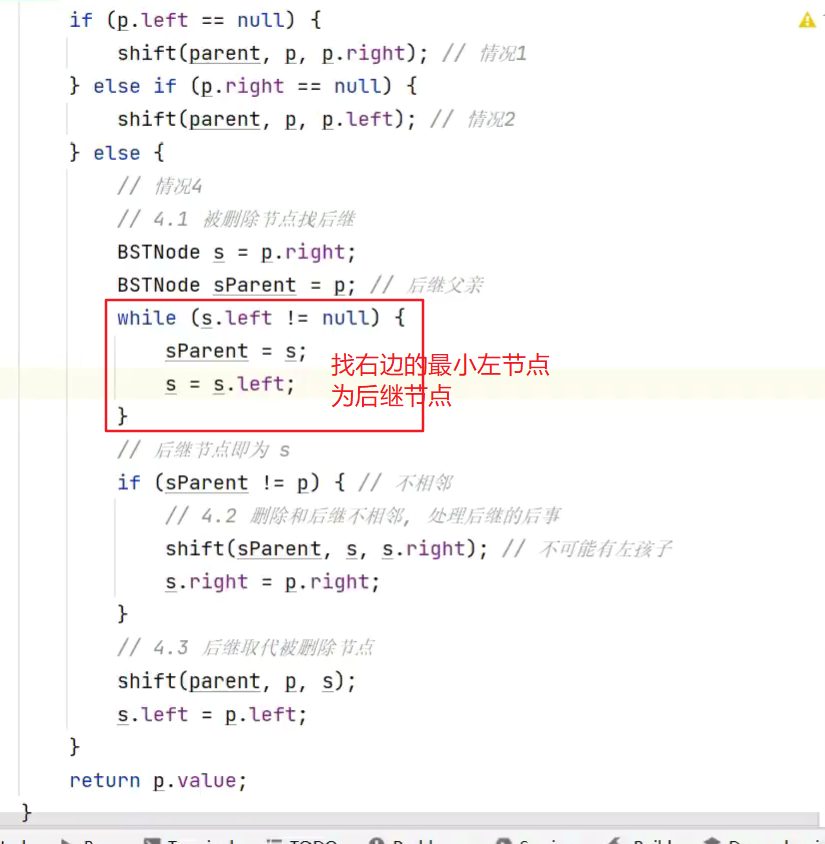
李代桃僵




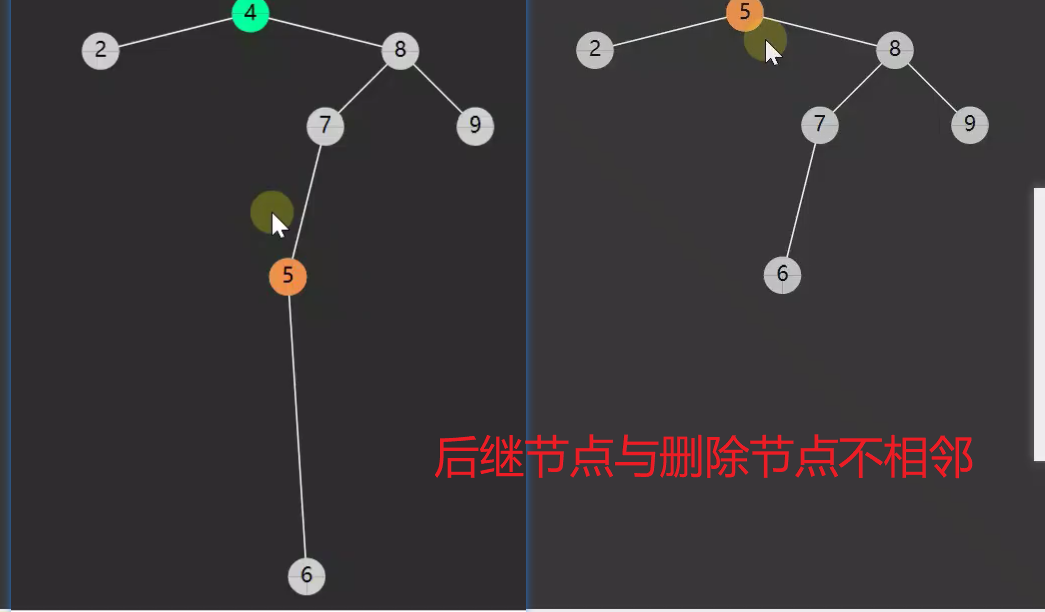
有两个孩子，李代桃僵，用后继节点的值取代原节点，二者交换，这样只需删除更换后的原节点（现在后继节点的位置，而后继节点肯定是没有孩子或者只有一右孩子

失衡调整

删除黑色节点会失衡，删除红色节点不失衡

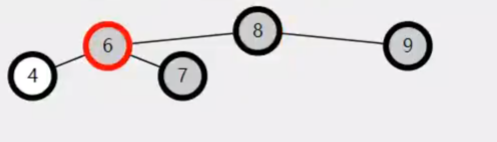
双黑（删除节点和剩余节点（null也是黑色）都是黑色节点，删除后少了一个黑

case3 过渡态，调节为case4/5

旋转，一个侄子节点变兄弟节点

旋转之后，恢复平衡，再进入case4/5

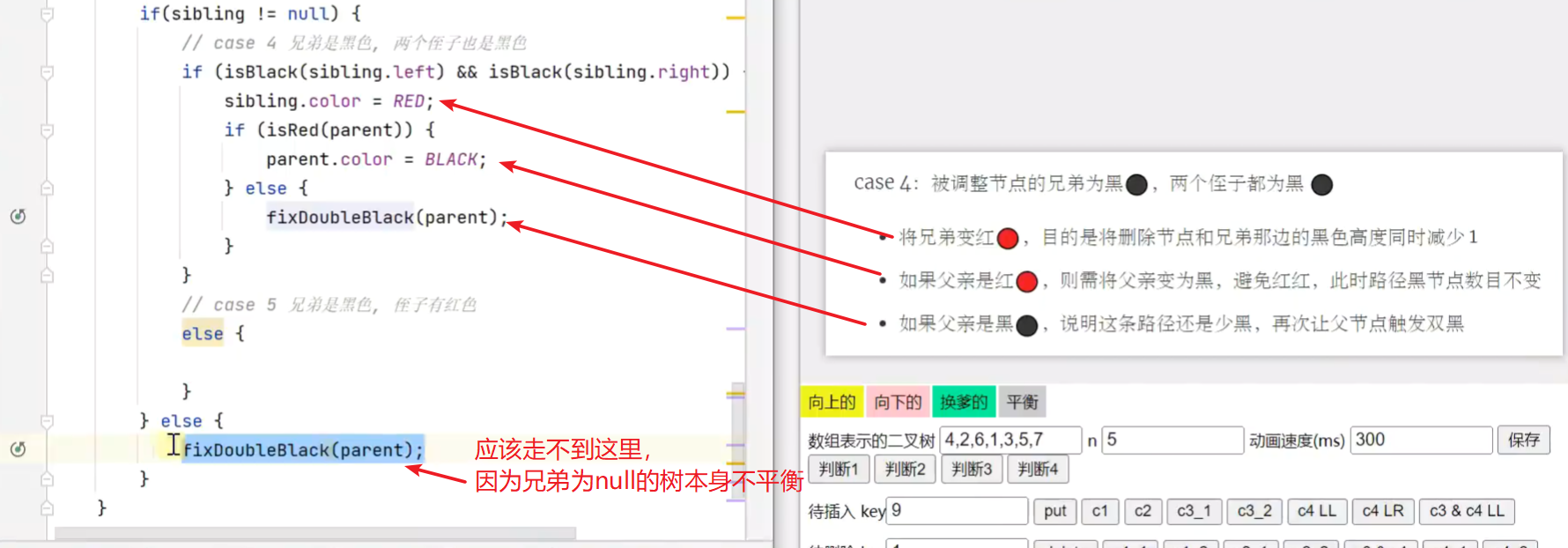
case4

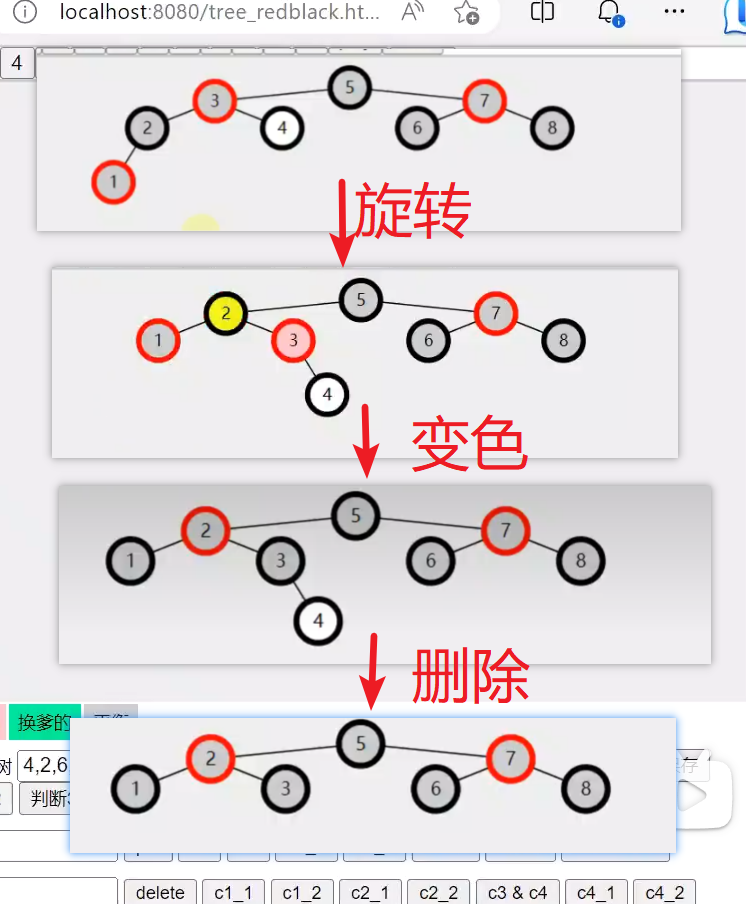
case5

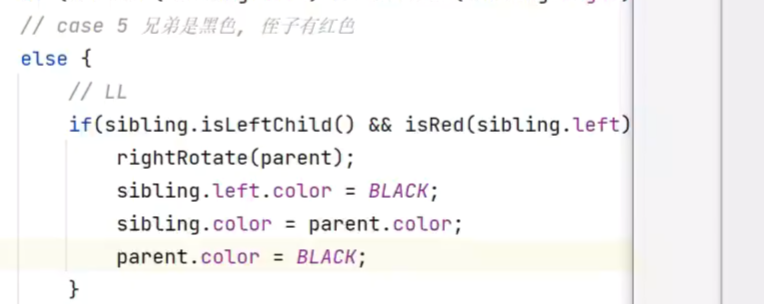
LL

1.删除节点的侄子节点的颜色变为黑色
2.兄弟节点的颜色变为父节点的颜色

3.删除节点的父节点变为黑色，因为原删除节点是黑色，删除后会少一个黑色，故需要父节点变色补回

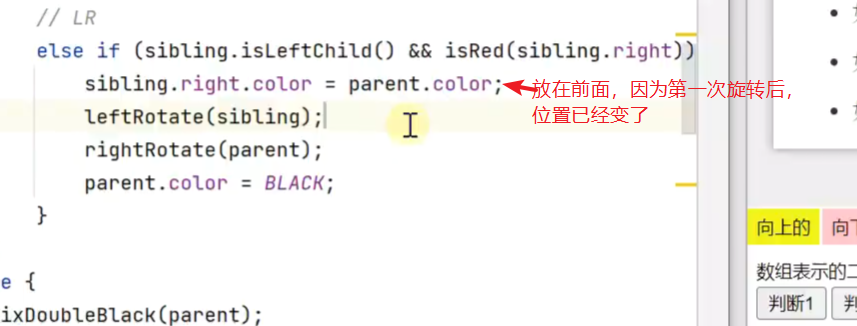
LR

RR和RL同理，因为四个方法都要将父节点颜色变为黑色，所以提出来放在外面

若有兄弟节点右两个红色子节点，也可以用上面的

posted @ 2023-08-13 18:58 Miku831 阅读(28) 评论(0) 收藏举报

刷新页面返回顶部

Data structure and algorithm-One

堆

公告