差分约束

对于给定的一系列的约束条件（例如x>y,y>z），然后我们要找到满足条件的可行解（或最值解），此时我们可以将约束条件转换为建边，用最短路算法解决

洛谷P3275 [SCOI2011] 糖果

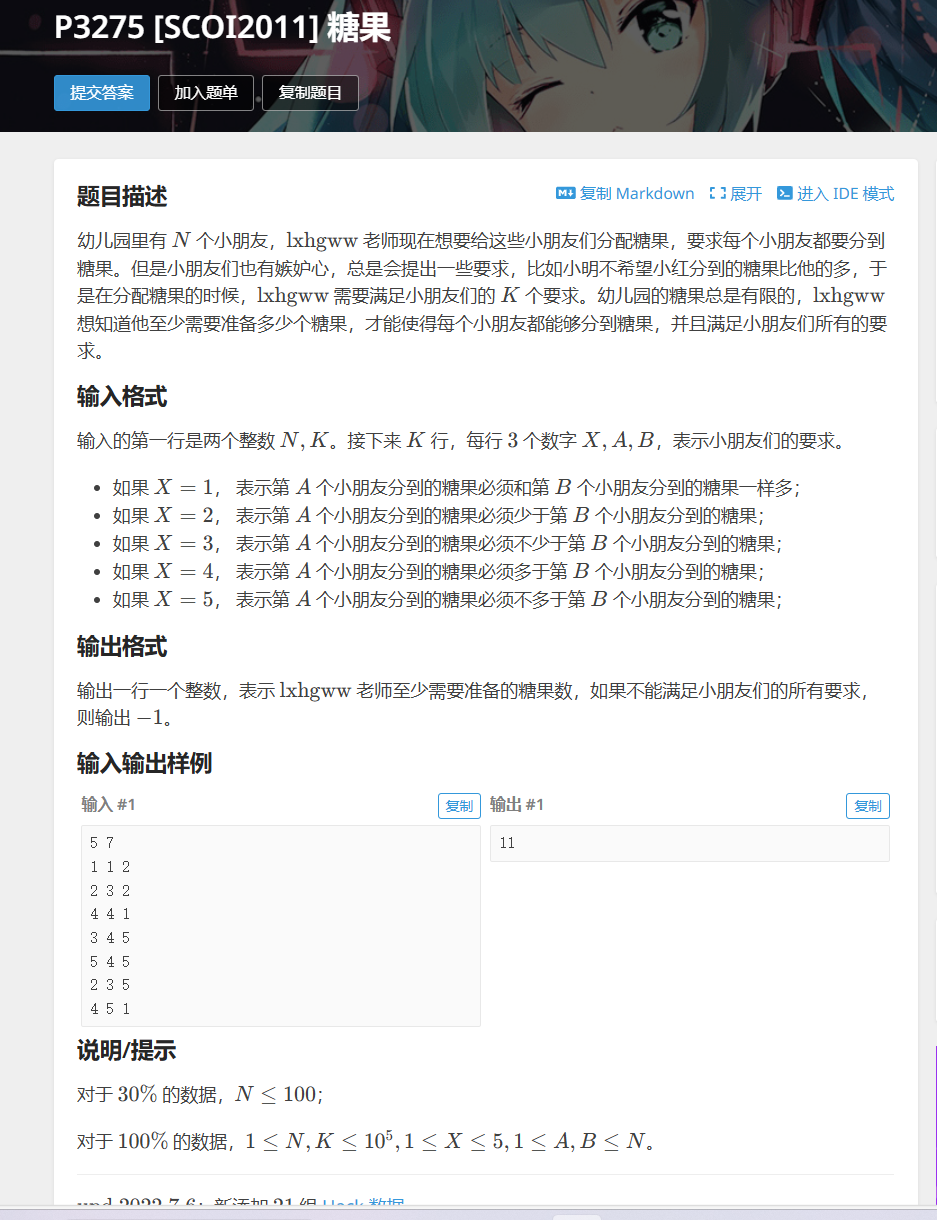
这题简单的差分约束其实不能ac，不过问题不大（
我们这里可以将五种情况看成五个不等式
比如X=1，那么A=B;
x=2,那么A<B;
x=3,A<=B
由于糖果都是整数，因此A<B我们也可以看成A+1<=B。我们如果想求b最低需要多少糖果，那么在已知A的糖果数的情况下，将其加一就是答案。因此我们可以转换为从A向B连一条长度为1的边，到B的距离就是他需要的最少糖果
不过这里需要注意的是，我们要求的应该是最长路而不是最短路。因为我们要保证满足所有条件，不过把spfa改一下就行了
还有一个点就是每个人都有糖果，也就是最小为1，因此新建一个虚拟节点0，向所有人都建一条长度为1的边，并且从0开始搜索。
代码如下，后面铸币n和k搞反了查了半天

点击查看代码

#include<bits/stdc++.h>
using namespace std;
//#define int long long
const int maxn=2e5+10;
int tot=0,head[maxn],nxt[maxn],to[maxn],w[maxn];
int cnt[maxn],dist[maxn];
int n,k;
bool vis[maxn];
void add(int x,int y,int z)
{
	tot++;
	nxt[tot]=head[x];
	w[tot]=z;
	to[tot]=y;
	head[x]=tot;
}
queue<int> q;
bool spfa()
{
	memset(dist,-0x3f,sizeof(dist));
	dist[0]=0;
	q.push(0);
	vis[0]=1;
	while(!q.empty())
	{
		int t=q.front();
		q.pop();
		vis[t]=false;
		for(int i=head[t];i;i=nxt[i])
		{
			int y=to[i];
			if(dist[y]<dist[t]+w[i])
			{
				dist[y]=dist[t]+w[i];
				cnt[y]=cnt[t]+1;
				if(cnt[y]>n+1) return false;
				if(!vis[y]) 
				{
					q.push(y);
					vis[y]=1;
				}
			}
		}
	}
	return true;
}
void youlinaixu()
{
	cin>>n>>k;
	for(int i=1;i<=k;i++)
	{
		int x,a,b;
		cin>>x>>a>>b;
		if(x==1) add(a,b,0),add(b,a,0);
		if(x==2) add(a,b,1);
		if(x==3) add(b,a,0);
		if(x==4) add(b,a,1);
		if(x==5) add(a,b,0);
	}
	for(int i=1;i<=n;i++)
	{
		add(0,i,1);
	}
	if(!spfa())
	{
		cout<<-1;
		return;
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
	//	cout<<dist[i]<<endl;
		ans+=dist[i];
	}
	cout<<ans;
}
signed main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int t=1;
	//cin>>t;
	while(t--)
	{
		youlinaixu();
	}

	return 0;
}