反悔贪心

反悔贪心

反悔贪心，顾名思义是可以反悔的贪心算法，具体来说，我们在直接贪心的过程中不一定能得到正确答案，而反悔贪心的本质就是通过一些操作使得我们在做出一些决定后可以撤销之前的决定

NC50439

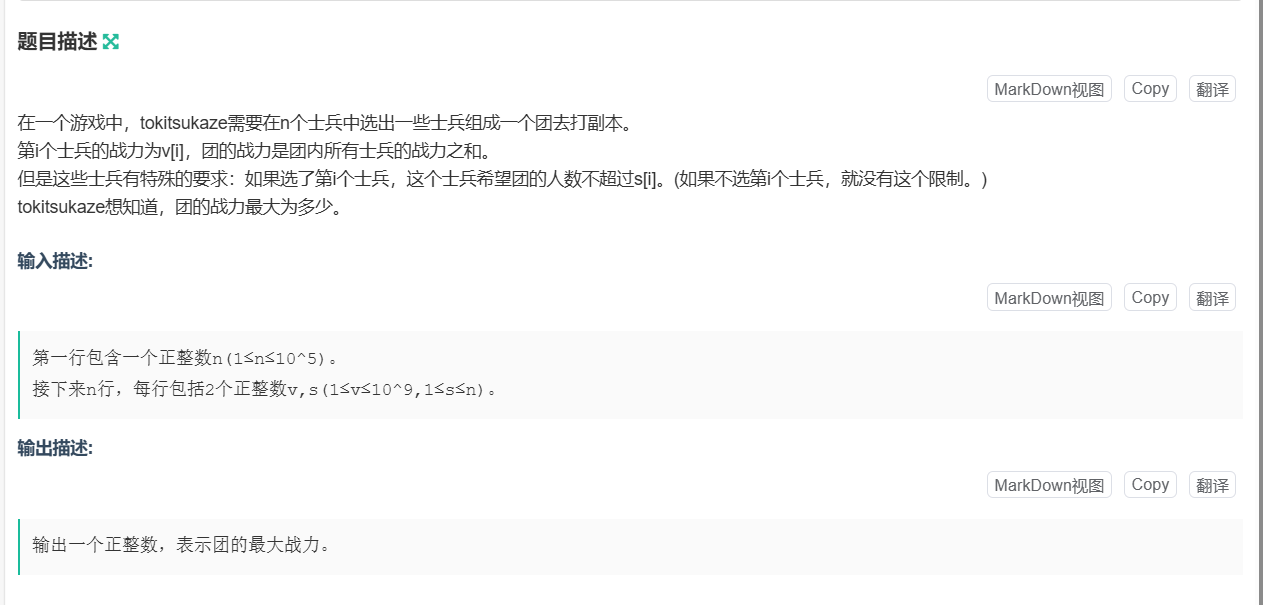
这道题目的特殊点主要在于每个士兵都希望团人数不超过一定数量

不过贪心仍然比较明显，我们第一直觉肯定是从v较大的开始选

但直接按照原顺序开始选的话显然是不正确的，因为在遇到较小的s[i]的时候，我们可能会舍弃掉最终答案中的值

也就是出现这种情况：假设最终答案士兵数量为5，那么我们在动态统计答案时，若遇到si<5的值，便可能会删去答案数组中的值，并且之后不会再统计进去，出现这样情况的最主要原因是队列人数取决于当前队伍中si的最小值

因此我们考虑将si从大到小排序枚举，并用优先队列维护当前队列的最大值

这样我们的队列人数从第一次满之后，一定是逐渐减少的

队列人数第一次满后，人员发生缩减当且仅当出现这种情况：在削减一定人数的情况下，加入当前士兵战力能使得总战力提高，也就是一个顶好几个

并且在后面的值也不会影响，因为之后的所有si都小于等于当前队伍人数

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
const int maxn=1e5+10;
struct node
{
//	int id;
	int v;
	int s;
}a[maxn];


priority_queue<int, vector<int>, greater<int>> q;

bool cmp(node x,node y)
{
	return x.s>y.s;
}
signed main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
//		a[i].id=i;
		scanf("%lld%lld",&a[i].v,&a[i].s);
	}
	sort(a+1,a+n+1,cmp);
	int sum=0,ans=0;
	for(int i=1;i<=n;i++)
	{
		//cout<<a[i].v<<' '<<a[i].s<<endl;
		q.push(a[i].v);
		sum+=a[i].v;
		while(q.size()>a[i].s)
		{
			sum-=q.top();
			q.pop();
		}
		ans=max(ans,sum);
	}
	cout<<ans;
	return 0;
}

[JSOI2007]建筑抢修

考虑几种贪心策略

1.按修理时间长短排序

2.按最晚开始时间排序（结束时间减去需要时间）

3.按截止时间排序

首先考虑第一种，即先做时间短的，但时间短的有可能截止时间很晚，此时肯定是将时间短的放到后面做比较优先

考虑第二种，按最晚开始时间排序，我们用优先队列维护当前已经修理的建筑，当遇到新建筑时我们查看当前时间是否小于最晚开始时间，若小于则直接加入，否则与队列中修理时间最长的建筑比较并决定是否替换。乍一看好像没什么问题，但我们可以看这样一组数据

3
10 16
17 36
9 35

按这种方法排序的顺序是 10 17 9 ，最晚开始时间分别是6 19 26

我们分别加入10,17，此时时间为27，与26比较发现无法再加入

但我们如果按10 9 17的顺序加入，会发现能够正好全部加入进去

造成这种情况的原因是按这种排序方式，后面的元素在判断是否加入时有可能会因为截止时间不如已经加入的元素优而导致无法加入

感性理解一下，对于相同的任务来说，需要的总用时是相同的，因此我们会期望先把截止时间较早的先做完，把截止时间靠后的放在后面

所以我们考虑按截止时间排序。如果当前总时间加上该建筑需要时间小于截止时间就直接加入，否则看目前已有的建筑中是否有修理时间大于该建筑时间的建筑。若有则当前建筑一定比该建筑优，直接替换即可

代码与上一题较为类似，因此不做展示

Buy Low Sell High

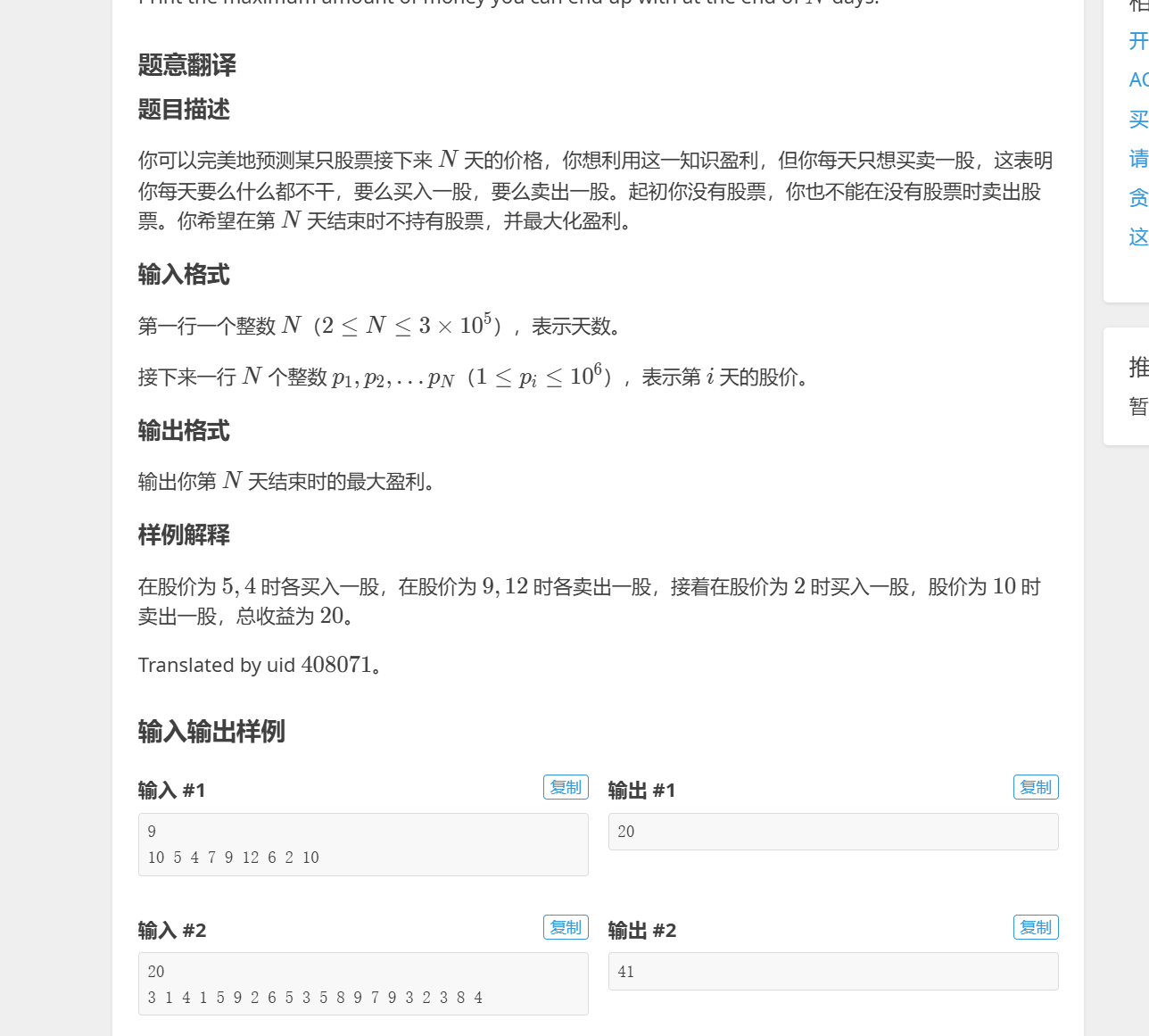
我们每天只能进行一种操作：买入或卖出一股，或是什么都不做，并且这里我们希望在结束时不持有股票

比较容易想到的是贪心买比较小的然后对于每个比较小的数选择它之后股价比最大的一天卖出

但我们这里不清楚该如何定义“较小”，并且还有一个限制是结束时不能持有股票

如果我们时刻统计当前手上股票数量并与剩余数量进行比对，则过于麻烦且正确性未知，并且我们也不知道以什么基准进行维护

因此我们考虑将买入和卖出进行“捆绑销售”，具体而言，我们不单独统计买入的股票，而是在卖出时选择一个最小的股票进行买入，这样就不会产生股票剩余问题

接下来问题就是，应该在何时买入？一个想法是从前往后遍历股票，并用优先队列小根堆存储所有可能被买入的股票，当前股票大于队头时则卖出。

但这样又会产生一个问题，形如 1 2 3这样的数据，显然是在第一天买入并且在第三天卖出时收益最大，但按我们的想法会在第一天买入第二天卖出

所以我们这里要想办法“反悔”，也就是像之前两道题一样替换掉队列中的数据，将第二天卖出改成第三天卖出

具体如何替换？我们考虑到，在遍历到2的时候，1已经是被卖出的状态，2是买入的状态。那么，我们如果再卖出2，并且买入3，就相当于卖出1买入3

因此我们只需要在替换的时候再将2加入到队列里，也就是作为一个备选的可卖出的物品。这样就给每次的替换提供了反悔的可能

代码比较简洁，思路不太好想

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
priority_queue<int,vector<int>,greater<int>> q;
signed main()
{
	
	int n;
	cin>>n;
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%lld",&x);
		q.push(x);
		if(q.top()<x)
		{
			ans+=(x-q.top());
			q.push(x);
			q.pop();
		}
	}
	cout<<ans;
	return 0;
}