字符串
我要成为字符串领域大神!
trie树/字典树
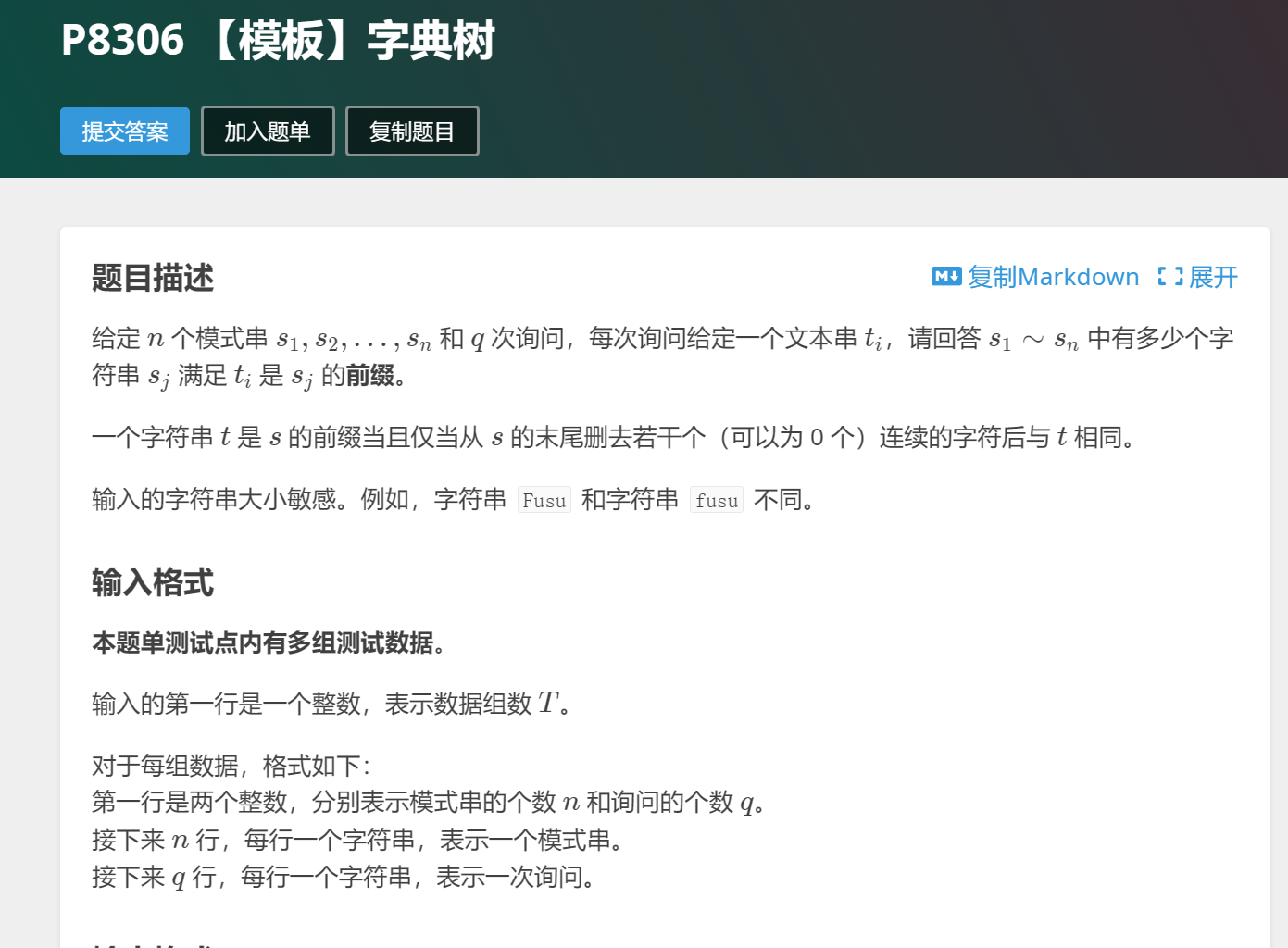
字典树是什么思想?我们先设定一个根节点,一般为0,每次加入新字符串时都与其相连。比如我们要插入string,看起来就是这样
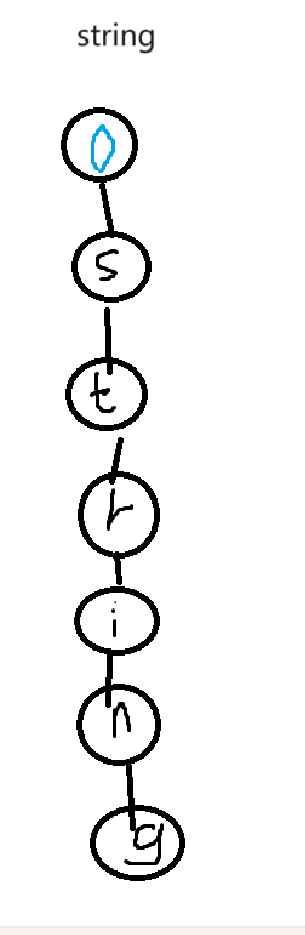
然后如果我们又插入一个strange,就会变成这样
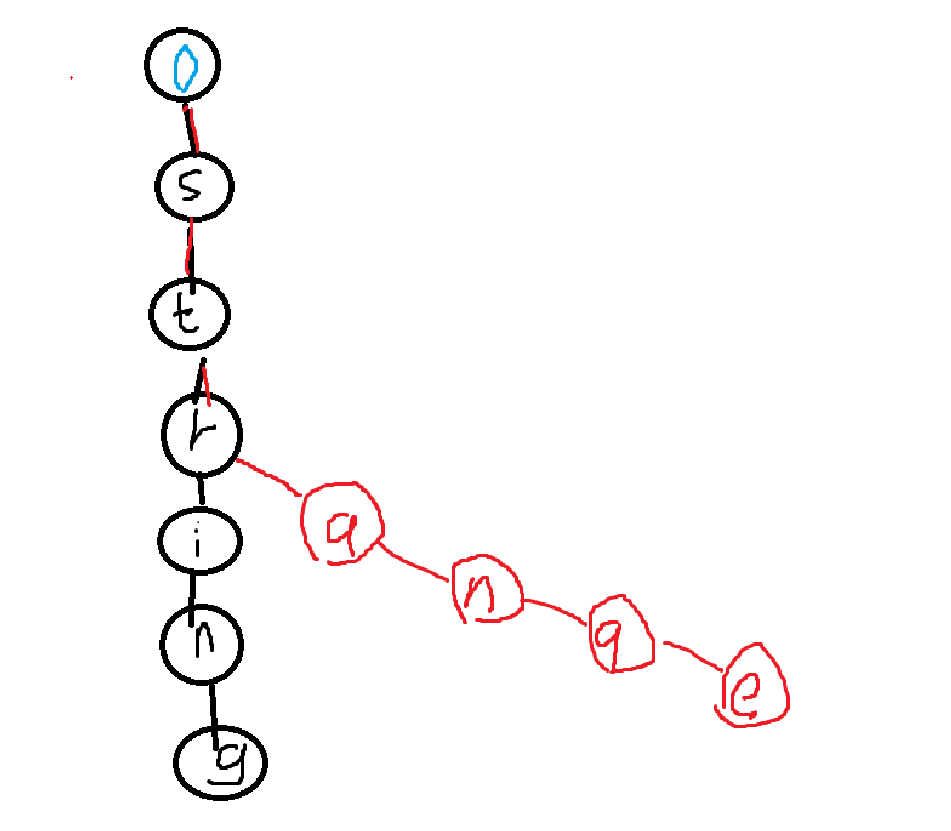
也就是说插入的时候可以直接继承志曾经出现过的前缀部分,思想就是这么个思想
具体实现就是建一个二维数组son[maxn]k,son[i][j]表示以i为父节点,他的字符为j的子节点的编号。什么叫字符为j?简单来说就是将字符种类转换为数字。比如如果只有小写英文字母,我们就会把a到z转换为0到25,如果有小写和大写字母,就转换为0到51,以此类推。
对于每个插入,遍历字符串,存在则继续遍历,不存在就新建叶子结点。对于本题则每次遍历都给路径都加1,那样对于每个查询,遍历到结尾时结尾上的值就是答案个数。
多测每次对数组清空
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e6+10;
int t,idx;
int a[maxn],cnt[maxn],son[maxn][65];
char str[maxn];
int trans(char x)//transform
{
if(x>='a'&&x<='z') return x-'a';
if(x>='A'&&x<='Z') return x-'A'+26;
if(x>='0'&&x<='9') return x-'0'+52;
}
void ins(char str[])//insert
{
int p=0;
for(int i=0;str[i];i++)
{
int now=trans(str[i]);
if(!son[p][now]) son[p][now]=++idx;
p=son[p][now];
cnt[p]++;
//cout<<cnt[p]<<endl;
}
}
int query(char str[])
{
int p=0;
for(int i=0;str[i];i++)
{
int now=trans(str[i]);
if(!son[p][now]) return 0;
p=son[p][now];
}
return cnt[p];
}
int main()
{
cin>>t;
while(t--)
{
int n,q;
scanf("%d%d",&n,&q);
for(int i=0;i<=idx;i++)
for(int j=0;j<=64;j++)
son[i][j]=0;
for(int i=0;i<=idx;i++)
cnt[i]=0;
idx=0;
for(int i=1;i<=n;i++)
{
scanf("%s",str);
ins(str);
}
for(int i=1;i<=q;i++)
{
scanf("%s",str);
printf("%d\n",query(str));
}
}
return 0;
}
01trie
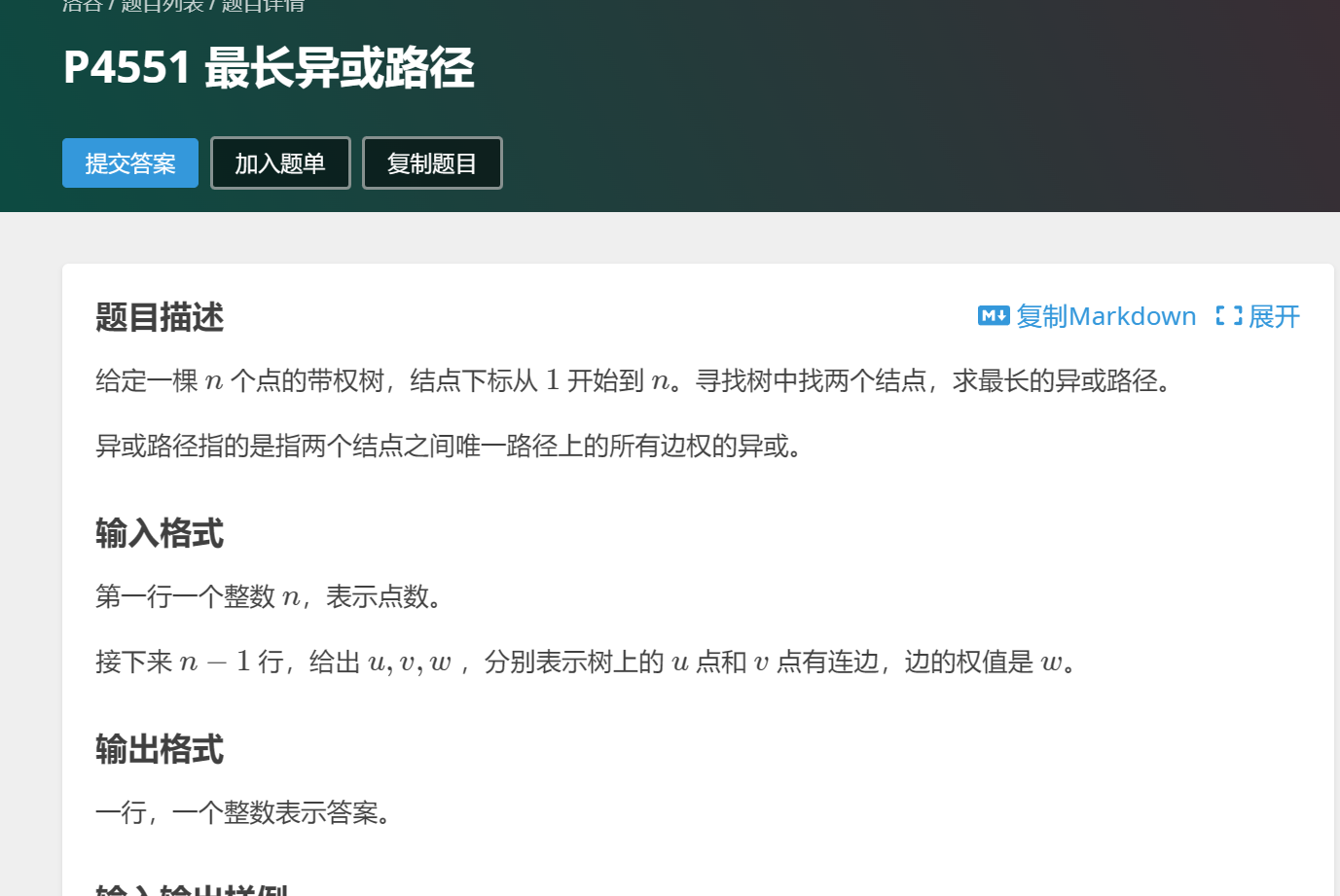
题意如图所示。
我们要求树上任意两点路径的最大异或和。首先,两个相同的数异或等于0,然后,一个数异或0等于它本身。
也就是说,ab==(ac)(bc)。
也就是说,我们要求从u点到v点的异或路径和,可以任意指定一个根节点,并把每个点到根节点的路径异或和都求出来,假如根节点为o,那么u到o的路径异或和与v到o的路径异或和进行异或运算的值就等于u到v的路径异或和(因为到根节点的重复部分异或为0被抵消)。
然后问题就转化成了,我们已知n个值,从这之中挑两个进行异或运算,求最大异或的值。
求最大异或一般用trie树。因为异或是按位异或,并且每位只有0和1,当每位不同时结果为1.我们要求异或最大值,自然是令高位尽量为1,也就是对于每个搜索的值的每一位都找相反的数。代码如下
构建时i从31到0主要是因为01串和普通字典树不一样,不是第一位与第一位匹配,第二位与第二位....而是末位匹配,因此要保证末位一一对应。
由于每个数转化为二进制最多有30位左右,一共有n个数,因此要开n<<4的字典树数组
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int head[maxn<<1],nxt[maxn<<1],tot=0,w[maxn<<1],to[maxn<<1],sum[maxn<<1];
void add(int x,int y,int z)
{
tot++;
w[tot]=z;
nxt[tot]=head[x];
to[tot]=y;
head[x]=tot;
}
int n;
void dfs(int x,int fa)
{
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y!=fa) {sum[y]=sum[x]^w[i];dfs(y,x);}
}
}
int m[maxn<<4][2],idx=0;
void work(int x)//将x转化为01串构建字典树
{
int root=0;
for(int i=31;i>=0;i--)
{
bool y=x>>i&1;
if(!m[root][y]) m[root][y]=++idx;
root=m[root][y];
}
}
int ans=0;
void query(int x)
{
int sum=0,root=0;
for(int i=31;i>=0;i--)
{
bool y=x>>i&1;
if(m[root][y^1])
{
sum+=1<<i;
root=m[root][y^1];
}
else root=m[root][y];
}
ans=max(ans,sum);
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
dfs(1,0);
for(int i=1;i<=n;i++)
{
work(sum[i]);
}
for(int i=1;i<=n;i++)
{
query(sum[i]);
}
cout<<ans;
return 0;
}
扩展kmp(z函数)

由于我很懒,就直接贴图了


我们维护一个区间,区间内的数是已经确定和前缀里等长的区间完全相同的,如果z[i-l+1],即对应当前i的点的z值小于区间从i到r的长度,就直接继承状态。若大于,就先继承整个区间,然后再从区间往后暴力匹配是否相同。
匹配完成更新z[i]后,如果发现i+z[i]-1已经超过了r,说明可以匹配的区间需要更新,则更新l和r
对b串进行自匹配结束后,我们要将它与a串进行匹配。大体内容类似,就是把b串作为前面的串,将a串不断枚举后缀操作即可(注意匹配时不能超过两个串的边界)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e7+10;
int z[maxn],p[maxn];
string a,b;
int sa,sb;
//维护z[i],意为对于i来说(i,i+z[i]-1) 为 i的匹配段,我们动态维护当前最右边的一段。
void workz(string s)
{
z[1]=sb;
for(int i=2,l=0,r=0;i<=sb;i++)
{
if(i<=r) z[i]=min(z[i-l+1],r-i+1);//当盒子右边缘在后面时,若前缀中对应的z[i-l+1]加上i后没有超出盒子则直接继承,超出则先继承盒子部分,其余暴力匹配
while(s[1+z[i]]==s[i+z[i]]) z[i]++;//暴力匹配是否相同
if(i+z[i]-1>r) l=i,r=i+z[i]-1;//若相同的前缀超出了盒子右边界,则更新盒子边界。
}
}
void workp()
{
for(int i=1,l=0,r=0;i<=sa;i++)
{
if(i<=r) p[i]=min(z[i-l+1],r-i+1);
while(a[i+p[i]]==b[1+p[i]]&&1+p[i]<=sb&&i+p[i]<=sa) p[i]++;
if(i+p[i]-1>r) l=i,r=i+p[i]-1;
}
}
int ans1=0,ans2=0;
signed main()
{
cin>>a>>b;
sa=a.size(),sb=b.size();
a=" "+a;
b=" "+b;
workz(b);
workp();
for(int i=1; i<=sb; i++)
ans1^=i*(z[i]+1);
for(int i=1; i<=sa; i++)
ans2^=i*(p[i]+1);
cout<<ans1<<endl<<ans2;
return 0;
}
最小表示法
这是个求什么用的呢,就是给你一个序列,然后把首尾相接形成环,求以哪个点为起点可以使得序列最小。
如果暴力匹配复杂度是n方无疑,我们该如何用On的复杂度解决?
我们首先想到的肯定是将数组加长,即破环为链
按照暴力匹配的思想,我们会将原序列复制成两个(实际并没有,只是方便理解),然后令i在第一个上跑,j在第二个上跑,i表示以i为起点,长度为n的序列,j同理。大概是这么个感觉
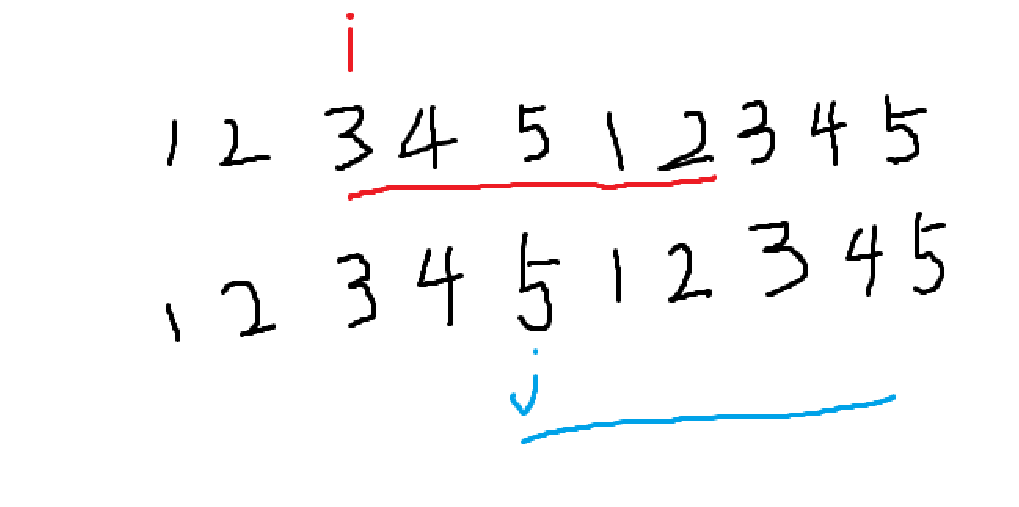
最小表示法也是这样,不过在i和j的基础上新增一个k。我们首先确定i和j,然后做如下操作:
k从0开始,比较a[i+k]和a[j+k]的值,若相同,则令k++。
若不同,则:
1.若此时a[i+k]>a[j+k],则说明以(i+k)点为起点的序列一定比(j+k)为起点的劣,此时我们令i直接跳转到i+k+1.为什么这样做呢?
我们来看看我们跳过了哪些。
显然,我们把所有的以(i,i+k)为起点的串都跳过了。为什么呢?因为我们要寻找的是最小序列,我们已经确定了a[i+k]>a[j+k],那么对于每个我们跳过的串,必然能在当前的以(j,j+k)为起点的序列中找到更优解。
比如如果此时的匹配情况是这样:
5432
5431
2显然大于1,我们就直接将i跳转到2后面的位置。因为:
对于前缀为5432的序列,有5431比它优秀
对于前缀为432的序列,有431比它优秀
对于前缀为32的序列,有31比它优秀.....
所以我们可以将i跳转到i+k+1
反过来也是一样,j+k上的数比较小时j可以跳到j+k+1。
当然还得考虑相等的情况,此时任意选一种即可。
并且如果我们发现i和j相等,说明他们后面完全相等,不需要匹配,此时令任意一个+1即可
代码如下
#include<bits/stdc++.h>
using namespace std;
const int maxn=7e5+10;
int a[maxn];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
a[i+n]=a[i];
}
int i,j,k;
for(i=1,j=2;i<=n&&j<=n;)
{
int k=0;
while(a[i+k]==a[j+k]&&k<n) k++;
if(a[i+k]>a[j+k]) i=i+k+1;
else if(a[i+k]<=a[j+k]) j=j+k+1;
if(i==j) j++;
}
int t=min(i,j);
for(i=t;i<=t+n-1;i++)
{
printf("%d ",a[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号