最长回文子串 洛谷 P3805 【模板】manacher算法

题目链接

这题与校赛的第二题AABB是一样的。同样也是最难的几道题。

本题是求给定的字符串的最长的回文子串长度。

我们先来看看求最长回文子串长度的方法。

 

方法一.暴力

 

直接暴力枚举一个起点和终点，再判断这个子串是否为回文。

枚举点的过程是n²，判断过程是n。总的为O（n³）的最坏情况。

这时间复杂度有点过分了。所以肯定不能那么做。

 

方法二.从内向外的思维

由于是回文子串。故为aba，或者abba这种形式。肯定存在一个对称点。

注意到如果子串中字符个数为偶数个，那么他的对称点为中间字符的空隙。

故我们需要枚举每个点和每个点之间的空隙。这个过程大致需要2n。

枚举对称点后，我们需要对每个对称点同时向左和向右寻找相同的字符个数，即为回文子串的长度。

故总的最坏时间复杂度为O(n²)

 

方法三.动态规划

令f[i][j]表示i到j之间的字符子串是否为回文串。若是则为1，若否则为0.

那么状态转移方程就是f[i][j]= f[i+1]f[j-1] (s[i]==s[j]), f[i][j] = 0 (s[i]!=s[j]).

其中令f[i][i]=1.

最后找出j-i最大且f[i][j]==1的值即可。

最坏时间复杂度为O(n²)

 

方法四.manacher算法（马拉车，想出这名字的是天才）

我们发现上述做法的时间复杂度都很高。

面对数据较大的时候经常会力不从心。

所以在14年还是15年就出现了个叫manacher的歪果仁发明了O（n）的manacher算法！

首先我们的思路还是和方法二差不多，找到对称中心，然后找对应回文串的半径。

首先不同的是，他在每个字符中加了个字符间隔，保证总体一定为奇数，防止了奇偶讨论的情况。

然后我们还可以在字符首尾各加上一个不同的字符，来简化边界情况。

如aabb就可以变成$#a#a#b#b#^。（注意#,$,^为原字符串中不可能出现的字符。我们观察到这里偶数个数的字符串变成奇数个数了！）

接下来我们令p[i]为新字符串中以每个字符为对称中心的半径。

由于字符串长度扩大了一倍，辅以画图和计算可以得出最后得出的答案，即原字符串以i为对称中心的回文子串长度为p[i]-1。

接下来的问题就是求p[i]了。

我们先要再借助两个数据，id和mx。

id为最右边一个回文子串的对称中心，mx 代表以 id 为中心的回文子串的右边界。（即mx为我们已经探索过的最大值）

这里搬一个别人的图示，方便理解

 

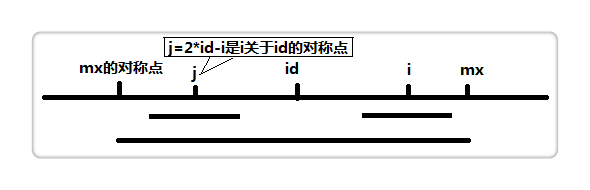
设j为i关于id的对称中心，由(i+j)/2=id，可得j=2*id-i。

 我们可以发现，由于mx为id的右边界，故id往右mx个单位和id往左mx个单位的值是相同的。

故i到mx的值和j到mx对称点的值也是相同的，都为mx-i。

那么如果j是一个半径小于mx-i的回文子串的对称中心，那么i也是。即p[i]=p[j].

如果j是一个半径大于mx-i的回文子串的对称中心，那么i只能保证是半径为mx-i的回文子串。即p[i]=mx-i.

所以p[i]=min(p[j],mx-i).

之后再对s[i+p[i]]和s[i-p[i]]进行循环判断即可。如果两者相等，则p[i]++、继续，否则就跳出。

需要注意的是如果不幸的mx不大于i，就令p[i]=1;（最开始初始化的时候也是这步操作）

如果mx小于i+p[i],那么就要更新边界和对称中心了，令mx=i+p[i],id=i;

最后找最大的那个p[i]即可。

时间复杂度分析：

我们这里把i从1~2n+1进行了遍历。

在其中p[i]已经根据mx和前面的数据在O（1）的请况下得到了一个初值。然后再对p[i]进行扩展，最多扩展到2n+1个。

然后mx也会跟着修改。

之后的p[i]的初值与修改后的mx挂钩

也就是说一共有2n+1+2n+1步操作。也就是最坏时间复杂度为O（n）

AC代码如下：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<cmath>
#define MAXN 11000005
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
char s[MAXN];
char ans[3*MAXN];//注意要在外面定义，在函数内定义空间会不够 
int  p[3*MAXN];
int Init(){//初始化更改字符串样式 
    ans[0]='$';//开始符号 
    ans[1]='#';
    int lentemp=strlen(s);
    int j=2;
    for(int i=0;i<lentemp;i++)    
        ans[j++]=s[i],ans[j++]='#';
    ans[j++]='&';//终止符号
    ans[j]='\0'; 
    return j;
}
int manacher(){
    int len=Init();
    int id,mx=0;
    int max_len=-1;
    for(int i=1;i<len;i++){
        if(i<mx)
            p[i]=min(p[2*id-i],mx-i);//初始化p[i] 
        else
            p[i]=1;
        while(ans[i-p[i]]==ans[i+p[i]])//继续找i的最大边界 
            p[i]++;
        if(mx<i+p[i]){//更新边界 
            id=i;
            mx=i+p[i];
        }
        max_len=max(max_len,p[i]-1);
    }
    return max_len;
}
int main(){
    scanf("%s",s);
    printf("%d",manacher());
    return 0;
}