YSU 2021年天梯赛&蓝桥杯校选赛--提高组 一些细节（时间的处理，大数是否记录，较大的幂级数的表示:(1ll<<n)）

这次校赛虽然水题较多。但还是铩羽而归（应该没用错词）。

那么毫无疑问归根结底还是我太菜了。

因此先来总结一下原先能A但没A出来的题或者A出来了但是走了弯路的题吧！

由于题目没有再度公开（老师说了会有重现。先等着吧）。不过题解里有些题写了题意（有些略掉了……）

因此就先混着来

T2： 签到（关于时间的一些处理）

本题是给一个上课签到的发出时间。小于等于10分钟内签到为考勤成功（出勤），10~20（包括20）分钟内签到为迟到（迟到），20+签到或者不签为缺席（缺勤）。

然后给出上课数，学生人数，每个学生签到时间。输出学生出勤数，迟到数，缺勤数。

之前本来一直是模拟。计算上课签到的发出时间的小时数，分钟数，秒数。然后和学生签到的进行对比。（如果在同一个小时……如果在下一个小时……）

但一直a不了。于是最后一小时又改了思路。改成了计算发出时间后10分钟，后20分钟的时候。在和学生签到的进行对比。

事实证明这样容错率高了不少。也终于A了。

但看了题解后才发现有个终极简单的思路被我忽略了（我是sb）

我们可以计算发出时间距离0.的秒数。即h*60*60+min*60+sec.

其值加600即是迟到的时限，加1200就是缺勤。计算出学生签到的秒数再比较下大小即可了。

#include<bits/stdc++.h>
using namespace std;
int n,m,s;
int main(){
    scanf("%d%d\n",&n,&m);
    int x,y,z;
    scanf("%d:%d:%d",&x,&y,&z);
    s=z+y*60+x*60*60;
    while(m--){
        int k;scanf("%d",&k);
        int ans1=0,ans2=0;
        for(int i=1;i<=k;i++){
            scanf("%d:%d:%d",&x,&y,&z);
            int t=z+y*60+x*60*60;
            if(t<=s+600)ans1++;
            else if(t<=s+1200)ans2++;
        }
        printf("%d %d %d\n",ans1,ans2,n-ans1-ans2);
    }
    return 0;
}

 

T3： 真正的“组合“数（关于大数是否记录）

这题的题面我忘了。但是我记得数据很大，而且要需要vis数组来判断他是否已经记录了。

但是远大于int的数据让我望而却步。

这里我们可以用unordered_map<ll,bool>s。

即给一个ll的值配对一个0/1的bool值来记录是否出现。

值得一提的是unorder_map的插入和查询平均复杂度都为O（1），最坏复杂度是O（n）的样子。

map的插入和查询复杂度为O（logn）。

其实本来想用set记录的。但是感觉数据太大时间复杂度过不了，然后后面就忘记这题了。

不过其实也是O（logn）。应该也是能过得吧……

解决了这一问题后DFS就行了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
unordered_map<ll,bool>Hash;
int n;
int A[30];
int dfs(int cur,int sum){
    Hash[sum]=1;
    for(int i=cur+1;i<=n;i++)
    dfs(i,sum+A[i]);
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&A[i]);
    dfs(0,0);
    printf("%d",Hash.size());
    return 0;
}

 

T5： 信息矩阵

本题的题意是有一个串s=1,然后令其后面加上一个~s（~s为将s中的0变成1,1变成0）。即

1 0 01 0110 01101001 0110100110010110。

求第i位的数是0还是1

我们可以发现。例如16这个数，是由8决定的，8是由2决定的，2是由1决定的。

15这个数是由7决定的，7是由3决定的，3是由1决定的。

中间隔了几个数就为异或1的次数。

可以发现规律。该数是由整个2的幂级数中的前面一半的想同位置异或得到。

也就是说得到最大的小于该数的2的幂级数。如15是8,16是8,17是16。

然后该数减去这个幂级数，对于得到的新数再进行同样的操作。直到减为1.

最后按操作次数决定结果是0还是1即可。

因此我们可以递归求解。

尽管这个思路我在考场已经一眼看穿（帅）

但还是一直wa（哭）

因为他i的数据范围丧心病狂到了10¹⁸。当然这也并没有逃过我的法眼。

一开始就注意到了并且直接开了long long。

但是没想到最后被pow这个求幂函数坑了。

由于pow的返回值是double。可能由于奇怪的类型转换

然后减去值的时候会出现奇怪的错误。如下为我测验的结果。

 

。

 

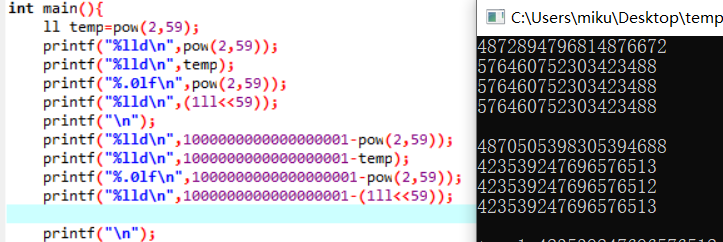
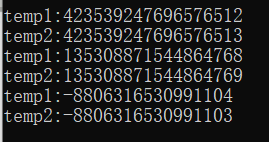
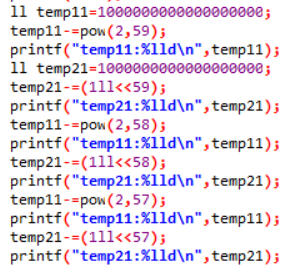
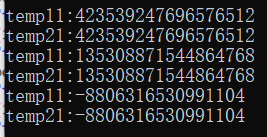
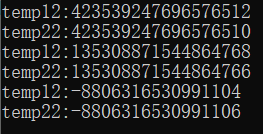
 也就是说1000000000000000001减去一个pow数是会有问题的。

1000000000000000000则没有。

但是999~99,999~98也会有……就很玄学。

所以我们还是尽量避免这种情况。

把pow（2,n）,改为(1ll<<n)吧。

注意由于<<运算符优先度较低，故很多时候要记得加上括号。

当然如果是pow(3,n)的话这种表示方法就失效了……

或许可以直接快速幂（反正也用不了几个码，还应该更快些）？

答案代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int query(ll x,int k){
    if(k==0)return 1;
    if(x>(1ll<<(k-1)))return query(x-(1ll<<(k-1)),k-1)^1;
    else return query(x,k-1);
}
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        ll x;
        scanf("%lld",&x);
        x++;
        int k=ceil(log2(x));
        cout<<query(x,k)<<endl;
    }
    return 0;
}

 

T6： 迪士尼在逃公主

本题的题意是：找到一个字典序最小的字符串，满足该字符串与给定的两个字符串对应位置的不同字符个数相同。

首先我们可以很快的发现，当给定的两个字符串对应位置相同时，自己找的那个取a即可。因为不管取什么都不会对不同字符个数的差值产生影响。

接下来我们定义一个数字x，代表与两字符串的不同字符个数的差值。如果与第一个的不同字符多就为正数，反之为负数。

则我们只用维护其为0即可。

因此我们从头开始找。如果该位置两字符串相同，则取a。

若不同，则遍历a~z。

对于每个字符串如果和两个字符串都不相同，则x不变，与1的相同，则x++，与2的相同，则x--。

再根据这个判断剩下的长度的字符串能否满足x=0，若能则取这个字符，若不能则回溯x，尝试下一个字符。

为了判断是否能满足x=0，我们还需要对两个字符串中相等的位置的数量进行记录。

令l为字符串总长，i为当前判断的下标，sum为当前下标之后的相等位置的数量。

故后面能对x的改变量为l-（i+1）-sum。若绝对值x小于这个值。则能满足要求。

因为我们是从前往后遍历的，对于无要求的都选了a，对于有要求的都按从a~z的字典序遍历且优先选择小的。

故最终得到的答案为字典序最小的且满足要求的字符串。

答案代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int T;
string s1,s2;
void solve(){
    cin>>T;
    int k=0;
    while(T--){
        cin>>s1>>s2;
        string s="";
        int sum=0;
        for(int i=0;i<s1.length();++i){
            if(s1[i]==s2[i]) sum++;
        }
        int l=s1.length();
        int x=0;
        for(int i=0;i<l;++i){
            if(s1[i]==s2[i]){
                s+='a';
                sum--;
            }
            else{
                int y=l-(i+1)-sum;
                int f=0;
                for(char c='a';c<='z';++c){
                    int t=x;
                    if(c==s1[i]) t++;
                    if(c==s2[i]) t--;
                    if(abs(t)<=y){
                        s+=c;
                        x=t;
                        break;
                    }
                }
            }
        }
        cout<<"Case "<<++k<<": "<<s<<endl;
    }
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    solve();
}