2020 BIT冬训-二分三分快速幂矩阵 J - One-Dimensional HYSBZ - 4688

Problem Description

考虑一个含有 N 个细胞的一维细胞自动机。细胞从 0 到 N-1 标号。每个细胞有一个被表示成一个小于 M 的非负

整数的状态。细胞的状态会在每个整数时刻发生骤变。我们定义 S(i,t)  表示第 i 个细胞在时刻 t 的状态。在

时刻 t+1 的状态被表示为 S(i,t+1)=(A×S(i-1,t)+B×S(i,t)+C×S(i+1,t) )  mod M ，其中 A,B,C 是给定的非

负整数。对于 i<0 或 N≤i ，我们定义 S(i,t)=0 。给定一个自动机的定义和其细胞在时刻 0 的初始状态，你的

任务是计算时刻 T 时每个细胞的状态。

 

Input

输入包含多组测试数据。每组数据的第一行包含六个整数 N,M,A,B,C,T ，满足 0<N≤50,0<M≤1000,0≤A,B,C<M,0

≤T≤〖10〗^9  。第二行包含 N 个小于 M 的非负整数，依次表示每个细胞在时刻 0 的状态。输入以六个零作为

结束。

 

Output

对于每组数据，输出N个小于M的非负整数，每两个相邻的数字之间用一个空格隔开，表示每个细胞在时刻T的状态。

 

Sample Input

5 4 1 3 2 0

0 1 2 0 1

5 7 1 3 2 1

0 1 2 0 1

5 13 1 3 2 11

0 1 2 0 1

5 5 2 0 1 100

0 1 2 0 1

6 6 0 2 3 1000

0 1 2 0 1 4

20 1000 0 2 3 1000000000

0 1 2 0 1 0 1 2 0 1 0 1 2 0 1 0 1 2 0 1

30 2 1 0 1 1000000000

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0

30 2 1 1 1 1000000000

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

30 5 2 3 1 1000000000

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Sample Output

0 1 2 0 1

2 0 0 4 3

212 10 9 11

3 0 4 2 1

0 4 2 0 4 4

0 376 752 0 376 0 376 752 0 376 0 376 752 0 376 0 376 752 0 376

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0

1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0

1 1 3 2 2 2 3 3 1 4 3 1 2 3 0 4 3 3 0 4 2 2 2 2 1 1 2 1 3 0

这题的思路是矩阵加速。如下图所示（时间有限直接画图板怼了qwq）：

 

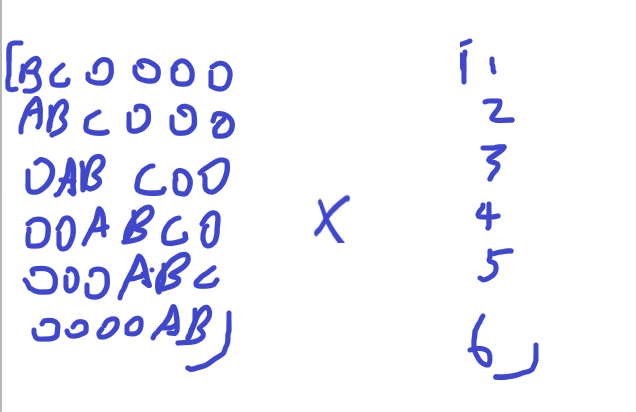
左边是转换矩阵，右边是原矩阵（1,2,3,4,5,6分别代表第几个数）。

求t时刻状态就是左边转换矩阵的幂。

故先对转换矩阵快速幂求取答案后再乘右边的原矩阵即可。

盲猜AC代码如下（BZOJ倒了……测试不了，样例都过了。。思路对了时间应该ok吧（心虚））

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m,a,b,c,t,s[55],transf[55][55],temp[55][55],ans[55][55],temp1,sss[55]; 
int main(){
    while(scanf("%d%d%d%d%d%d",&n,&m,&a,&b,&c,&t),n){
        memset(ans,0,sizeof(ans));
        memset(transf,0,sizeof(transf));
        for(int i=0;i<n;i++)
            scanf("%d",&s[i]);
        for(int i=0;i<n;i++){
            transf[i][i]=b;
            transf[i][i+1]=c;
            transf[i+1][i]=a;
        }
        for(int i=0;i<n;i++)
            ans[i][i]=1;
        while(t){
            if(t&1){
                for(int i=0;i<n;i++)
                    for(int j=0;j<n;j++){
                        temp[i][j]=0;
                        for(int k=0;k<n;k++){
                            temp[i][j]+=(ans[i][k]*transf[k][j])%m;
                        temp[i][j]%=m;
                        }     
                    }
                for(int i=0;i<n;i++)
                    for(int j=0;j<n;j++)
                        ans[i][j]=temp[i][j];
            }
            t>>=1;
            for(int i=0;i<n;i++)
                for(int j=0;j<n;j++){
                    temp[i][j]=0;
                    for(int k=0;k<n;k++)
                        temp[i][j]+=(transf[i][k]*transf[k][j])%m;
                    temp[i][j]%=m;
                }     
            for(int i=0;i<n;i++)
                for(int j=0;j<n;j++)
                    transf[i][j]=temp[i][j];
        }
        for(int i=0;i<n;i++){
            temp1=0;
            for(int j=0;j<n;j++)
                temp1+=(ans[i][j]*s[j])%m;
            temp1%=m;
            sss[i]=temp1;
        }
        for(int i=0;i<n;i++){
            printf("%d ",sss[i]);
        }
        printf("\n");
    }
    
}