二叉树的重建（前序+中序）（后序+中序）（层序+中序）

解决一个重要的问题：如果给定一棵二叉树的先序遍历序列和中序遍历序列，重建这棵
二叉树。
假设已知先序序列为pre1、pre2、…、pren，中序序列为in1、in2、…、inn，如图下图所
示。

 

 

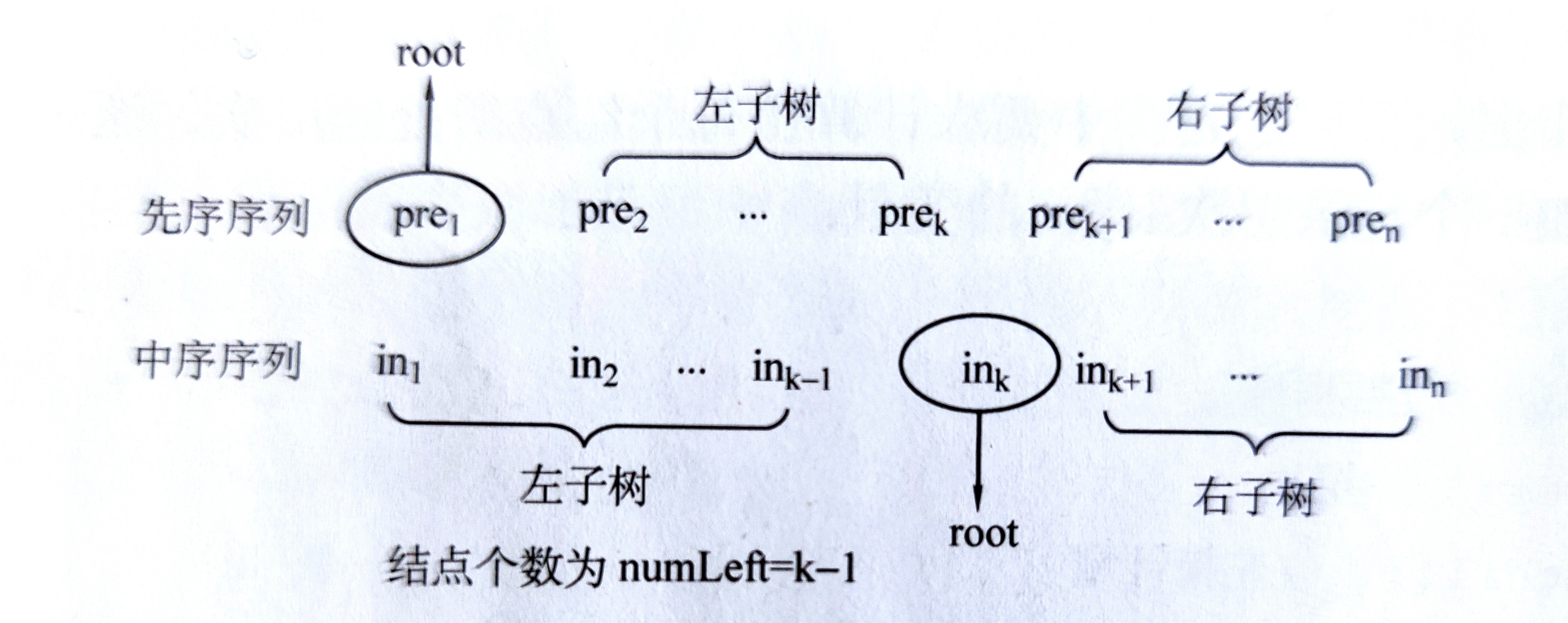
那么由先序序列的性质可知，先序序列的第一个元素pre1是当前二叉树的根结点。再由中序序列的性质可知，当前二叉树的根结点将中序序列划分为左子树和右子树。因此，要做的就是在中序序列中找到某个结点ink，使得ink = pre1，这样就在中序序列中找到了根结点。易知左子树的结点个数numLef = k - 1。于是，左子树的先序序列区间就是[2，k]，左子树的中序序列区间是[1，k - 1],右子树的先序序列区间是[k + 1，n]，右子树的中序序列区间是[k + 1，n]，接看只需要往左子树和右子树进行递归构建二叉树即可。

 

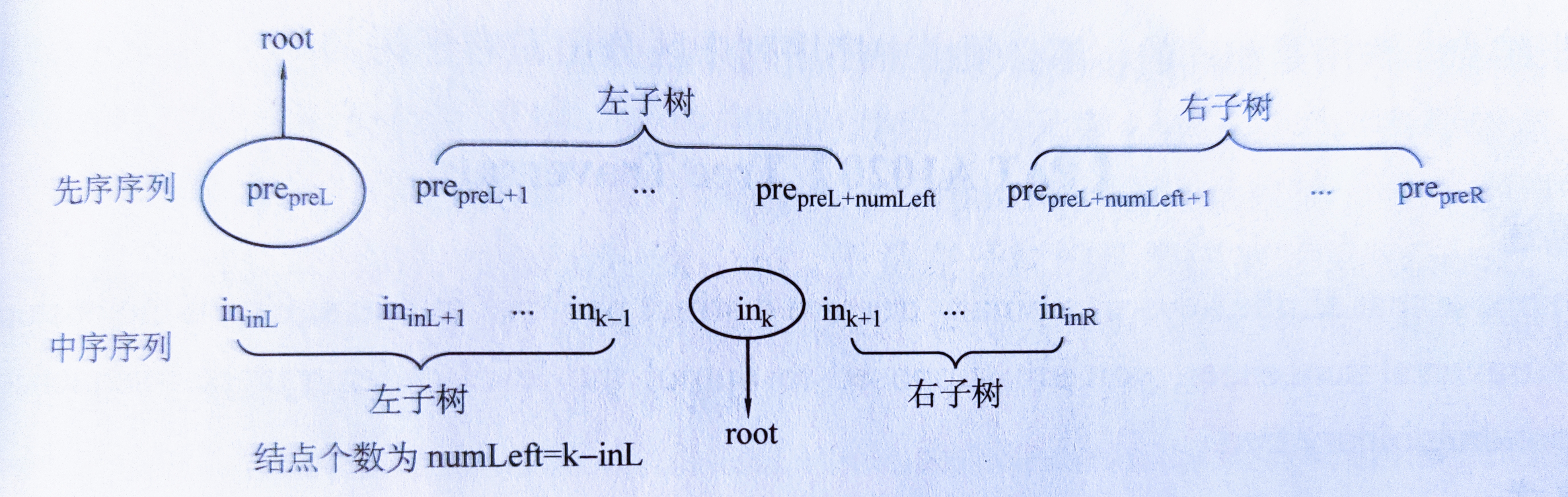
先序序列和中序序列或者后序序列和中序序列构建二叉树（两种构建的方法相似，都是一层循环找到根节点之后，左右子树进行递归后返回指针），之后再利用层序遍历（或者先序，后序）输出：

当前先序序列区间为[preL，preR]，中序序列区间为[inL,inR]，后序序列为[postL,postR]。

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 50;
int n,pre[maxn], in[maxn], post[maxn];//n代表节点个数
struct node {
    int data;
    node* lchild;
    node* rchild;
};
node* preincreate(int preL, int preR, int inL, int inR) {
    if (preL > preR) {
        return NULL; //因为为左闭右闭区间所以preL > preR代表区间长度为0，为空树；
    }
    node* root = new node;//创建一个新的节点来存放二叉树的根节点；
    root->data = pre[preL];//新节点的数据域的值为根节点的值。
    int k=0;
    for (k = inL; k <= inR; k++) {
        if (in[k]==pre[preL]) {//在中序序列中找到in[k]==pre[preL]的节点，此为根节点
            break;
        }
    }
    int numleft = k - inL;//左子树的节点个数。
    //思考:
    //左子树的先序区间[preL+1,preL+numleft],左子树的中序区间为[inL,k-1];
    root->lchild = preincreate(preL + 1, preL + numleft, inL, k - 1);
    //右子树的先序区间[preL+numleft+1,preR],右子树的中序区间[k+1,inR];
    root->rchild = preincreate(preL + numleft + 1, preR, k + 1, inR);
    return root;
}

node* postincreate(int postL, int postR, int inL, int inR) {
    if (postL > postR) {
        return NULL;
    }
    node* root = new node;//创建一个新的节点来存放二叉树的根节点；
    root->data = post[postR];//新节点的数据域的值为根节点的值
    int k=0;
    for ( k = inL; k <=inR; k++) {
        if (in[k] == post[postR]) {
            break;
        }
    }
    int numleft = k - inL;
    root->lchild = postincreate(postL, postL + numleft - 1, inL, k - 1);
    root->rchild = postincreate(postL+numleft  , postR - 1, k + 1, inR);
    return root;//返回根节点的地址
}

void BFS(node* root) {
    queue<node*> q;//队列中存放地址
    q.push(root);
    while (!q.empty()) {
        node* top = q.front();
        q.pop();
        printf("%d  ", top->data);
        if (top->lchild != NULL) q.push(top->lchild);//左子树非空
        if (top->rchild != NULL) q.push(top->rchild);//右子树非空
    }
}
int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &post[i]);
    }
    for (int i = 0; i < n; i++) {
        scanf("%d", &in[i]);
    }
    node* root = postincreate(0,n-1,0,n-1);//通过后序和中序创建树。
    BFS(root);//层序遍历输出
    delete(root);
    return 0;
}

由层序遍历和中序遍历重建二叉树 ,因为层序序列是按照层级进行排列的，每一层的节点都是下一层的根节点，因此通过遍历层序序列和中序序列找到层级优先级高的节点(层次低的，层序序列排在前面的)，再通过中序序列将其分为左右子树进行更深一层的递归遍历查找，直到达到递归基。

node* layerincreate(int ll, int lr, int inl, int inr) {
    if (inl > inr)
        return NULL;
    node* root = new node;//创建一个新的节点来存放二叉树的根节点。
    int i, j;
    if (inl > inr) {
        return NULL;//递归边界，中序序列的长度为零，子树为空树。
    }
    for (i = ll; i <= lr; i++) {//从层数低的节点（优先级高的节点）开始查找。
        bool f = false;//标记未找到
        for (j = inl; j <= inr; j++) {
            if (layer[i] == in[j]) {
                root->data = in[j];//将当前序列的根节点数据域赋值；
                f = true;
                break;//找到了并标记，立刻退出内层循环
            }
        }
        if (f) break;//找到当前中序序列中优先级最高的节点，后退出循环
    }
    if (j >=inl) root->lchild = layerincreate(0, n - 1, inl, j - 1);//通过递归对当前根节点的指向左子树根节点的指针进行赋值。
    if (j <=inr) root->rchild = layerincreate(0, n - 1, j + 1, inr);//通过递归对当前根节点的指向左子树根节点的指针进行赋值。
    return root;//返回当前序列的根节点。
}

void preOrder(node* root) {
    if (root == NULL) return;
    printf("%d ", root->data);
    preOrder(root->lchild);
    preOrder(root->rchild);
}

void inOrder(node* root) {
    if (root == NULL) return;
    inOrder(root->lchild);
    printf("%d ", root->data);
    inOrder(root->rchild);
}

void postOrder(node* root) {
    if (root == NULL) return;
    postOrder(root->lchild);
    postOrder(root->rchild);
    printf("%d ", root->data);
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &layer[i]);//输入层序序列
    for (int i = 0; i < n; i++)
        scanf("%d", &in[i]);//输入中序序列
    node* root = layerincreate(0, n - 1, 0, n - 1);
    preOrder(root);
    printf("\n");
    postOrder(root);
    return 0;
}

与上面类似的还可以，由层序遍历和中序遍历我们先递归求出先序序列，再由先序和中序重建二叉树。

#include<cstdio>
using namespace std;
const int maxn = 50;
int layer[maxn], in[maxn], pre[maxn];
int n,idx=0;
struct node {
    int data;
    node* lchild;
    node* rchild;
};

void makepre(int ll, int lr, int inl, int inr) {
    int i=0, j=0;
    //找出层序遍历中的根节点在中序序列中的位置 
    for (i = ll; i <= lr; i++) {
        bool f = false;
        for (j = inl; j <= inr; j++) { 
            if (layer[i] == in[j]) {
                pre[idx++] = in[j];//构造先序序列 
                f = true;//找到了先序排列的一个节点后退出循环。
                break;
            }
        }
        if (f) break;
    }
    //将刚加入先序序列的节点的左子树递归
    if (j > inl) makepre(ll, lr, inl, j - 1);
    //将刚加入先序序列的节点的右子树递归 
    if (j < inr) makepre(ll, lr, j + 1, inr);
}
//由先序和中序递归构造二叉树 
node* preincreate(int preL, int preR, int inL, int inR) {
    if (preL > preR) {
        return NULL; //因为为左闭右闭区间所以preL > preR代表区间长度为0，为空树；
    }
    node* root = new node;//创建一个新的节点来存放二叉树的根节点；
    root->data = pre[preL];//新节点的数据域的值为根节点的值。
    int k = 0;
    for (k = inL; k <= inR; k++) {
        if (in[k] == pre[preL]) {//在中序序列中找到in[k]==pre[preL]的节点，此为根节点
            break;
        }
    }
    int numleft = k - inL;//左子树的节点个数。
    //思考:
    //左子树的先序区间[preL+1,preL+numleft],左子树的中序区间为[inL,k-1];
    root->lchild = preincreate(preL + 1, preL + numleft, inL, k - 1);
    //右子树的先序区间[preL+numleft+1,preR],右子树的中序区间[k+1,inR];
    root->rchild = preincreate(preL + numleft + 1, preR, k + 1, inR);
    return root;
}
//先序遍历 
void preOrder(node* root) {
    if (root == NULL) return;
    printf("%d ", root->data);
    preOrder(root->lchild);
    preOrder(root->rchild);
}
//中序遍历 
void inOrder(node* root) {
    if (root == NULL) return;
    inOrder(root->lchild);
    printf("%d ", root->data);
    inOrder(root->rchild);
}
//后序遍历 
void postOrder(node* root) {
    if (root == NULL) return;
    postOrder(root->lchild);
    postOrder(root->rchild);
    printf("%d ", root->data);
}
int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &layer[i]);
    for (int i = 0; i < n; i++)
        scanf("%d", &in[i]);
    makepre(0, n - 1, 0, n - 1);
    node* root = preincreate(0, n - 1, 0, n - 1);

    preOrder(root);
    printf("\n");
    postOrder(root);
    return 0;
}

下一节：二叉树的静态实现