4 UVA11134 Fable Rooks & 传说中的车 题解

Fable Rooks

题面

在 \(n \times n\) 的网格中放置 \(n\) 个棋子，使得第 \(i\) 个棋子处在 \((x_1, y_1) , (x_2, y_2)\) 的矩形内，并且任意两个棋子不在同一行并且不在同一列。

求是否有解，如果无解输出 IMPOSSIBLE，否则输出每个棋子的位置，按照给出的顺序输出。

\(1 \le n\le 5000\)

题解

首先，因为 \(x,y\) 互不影响，所以我们可以分开考虑 \(x, y\) 方向的选点策略。

那么问题转化为：给定 \(n\) 个区间 \([a_i, b_i]\)，要求对每个区间选择一个点满足 \(a_i \le x_i \le b_i\)，并且每个对每个区间所选的 \(x_i\) 互不相同。

直观的想，我们希望选择的点所覆盖的区间尽可能少，因为如果覆盖的区间很多，那么可能会导致某些区间无点可选。

一个假思路是：按照区间左端点为第一关键字，右端点为第二关键字排序，从小到大选择能选的点。

hack：[1,3],[1,3],[2,2]

这个思路为什么假了？

我们只顾着选两个 [1,3] 从而导致 [2,2] 无点可选，如果我们先选 [2,2]，那么是不是就能够避免这种情况？

我们按照分析基本贪心的思路去分析，规定放的顺序为从小到大放：

先考虑包含关系的情况，\(a_1 \le a_2 \le b_2 \le b_1\)，那么我们一定是先放小区间，然后再考虑大区间，因为如果先放大区间，可能会抢占小区间本来就不多的位置，导致小区间无点可选。

然后再考虑相交关系

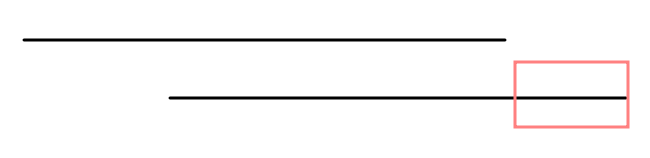
假如我们先在第一个区间中放点，那么第二个区间永远有机会放在红色框位置处。

如果我们先在第二个区间中放点，因为我们是从小到大放点，所以可能会导致第一个区间无点可选。

所以我们每次选择第一个区间放点。

那么贪心策略就是按照右端点从小到大排序，如果右端点相同，随便排即可（因为两个区间后面都不会比对方多出一段），然后对于每个区间，选择能选的最小点放即可。

我们也可以变换一下：从大到小放点，按照左端点从大到小排序，如果左端点相同，随便排即可。

时间复杂度 \(O(n^2)\)

code

#include <bits/stdc++.h>

using namespace std;

namespace michaele {
	
	#define rep(i, s, t) for (int i = s; i <= t; i ++)
	#define irep(i, s, t) for (int i = s; i >= t; i --)
	typedef pair <int, int> pii;

	const int N = 5e3 + 10;

	int n;
	struct node {
		int x, y, id;
		int ans;
	} a[N], b[N];

	bool vis[N];

	void solve () {
		while (cin >> n) {
			if (!n) break;
			rep (i, 1, n) {
				cin >> a[i].x >> b[i].x >> a[i].y >> b[i].y;
				a[i].id = b[i].id = i;
			}
			auto cmp = [](node &a, node &b) { 
				return a.x > b.x;
			};

			sort (a + 1, a + 1 + n, cmp);
			sort (b + 1, b + 1 + n, cmp);

			bool ok = 1;
			auto work  = [&](node *t) {
				fill (vis + 1, vis + 1 + n, 0);
				rep (i, 1, n) {
					bool fn = 0;
					irep (j, t[i].y, t[i].x) {
						if (!vis[j]) {
							vis[j] = 1;
							t[i].ans = j;
							fn = 1;
							break;
						}
					}
					if (!fn) {
						ok = 0;
						break;
					}
				}
			};
			work (a);
			work (b);
			if (!ok) cout << "IMPOSSIBLE\n";
			else {
				auto cmp2 = [](node &a, node &b) { return a.id < b.id; };
				sort (a + 1, a + 1 + n, cmp2);
				sort (b + 1, b + 1 + n, cmp2);
				rep (i, 1, n) {
					cout << a[i].ans << ' ' << b[i].ans << '\n';
				}
			}
		}
	}
}

int main () {

	michaele :: solve ();

	return 0;
}