30 S2模拟赛T3 对称区间 题解

对称区间

题面

给定一个长度为 \(n\) 的二进制串 \(S\)，你需要回答 \(q\) 个查询，每个查询属于以下两种类型之一：

1. 给定两个整数 \(l, r\ (1 \le l \le r \le n)\)，翻转每个 \(i \in [l,r]\) 的二进制位 \(S_i\)。
2. 给定三个正整数 \(l,a,b\ (1 \le l \le n, 1 \le a, b \le n - l + 1)\) ，你需要计算有多少个区间 \([u,v](1 \le u \le v \le l)\) 满足 \(S_{a + x - 1} = S_{b + x - 1}\) 对每个 \(x \in [u, v]\) 都成立，这些区间称为对称区间。

\(1 \le n, q \le 10^6\)

保证第 2 类查询的数量不超过 2500。

题解

我们可以先想想暴力怎么做？

\(n^2\) 暴力不难想到，直接暴力模拟两个操作，第二个操作有性质：对于一段连续的相同段，设其长度为 \(len\)，那么它对答案的贡献即为 \((len + 1) \times len / 2\) 。所以对于 2 操作，我们只需枚举每个位置，查看是否相同即可。

下面我们想如何优化这两个操作

因为 2 操作至多只有 2500 个，所以我们可以先优化 1 操作。

对于区间取反操作，我们可以用差分前缀和将修改优化为 \(O(1)\)。

但是对于每次操作 2，我们都需要再将序列还原。所以总时间复杂度为 \(O(q_1 + nq_2)\)。

现在的时间复杂度瓶颈集中在操作 2，其主要是由于对整个序列的还原以及查询太慢

所以我们考虑题目中给的序列有什么性质？

题目中给的是二进制串！

我们是不是可以用某个数来代替一段字符串，从而用位运算来优化区间异或以及两个字符串的比较操作。

是可以的，我们可以对原来的字符串分成长度为 \(B\) 的块，对于每个块，我们维护一个二进制数 \(b\)，用对 \(b\) 的操作代替对原串的操作。

对于操作 1，散块暴力，整块直接差分，时间复杂度 \(O(2Bq_1)\)。

对于操作 2，我们可以先遍历每个块，将整个序列还原。

然后我们不断取出长度为 \(B\) 的块对应的二进制数，记为 \(s1, s2\)，设 \(tmp = s1 \oplus s2\)，\(tmp\) 一定形如下图：

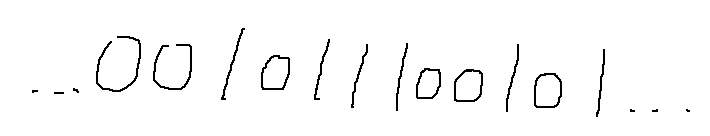
其中 0 表示匹配成功，1 表示匹配失败，所以我们直接按照公式分别计数即可。

为了防止再遍历一遍，我们可以事先将 \(tmp\) 对应的二进制数的贡献预处理出来。

• \(pre\) 前缀 0 数量，\(suf\) 后缀 0 数量
• \(val\) 中间 0 对答案的贡献

然后对于每个块就可以 \(O(1)\) 计算贡献。

所以操作 2 的时间复杂度降为 \(O(\frac n B q_2)\)

总时间复杂度即为 \(O(Bq_1 + \frac n B q_2 + B \times 2^B)\)，取块长为 16 ，大概是 2e8 左右，给了 4 秒时限，所以可过

code

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

namespace michaele {

    typedef long long ll;

    const int N = 1e6 + 10, B = 14, S = (1 << B);

    int n, m;
    int a[N], bel[N], b[N], L[N], R[N], tag[N];
    int pre[N], suf[N], val[N];
    
    // 按二进制输出，调试用
    void prt_bin (int x) {
        for (int i = 0; i <= 15; i ++) {
            if ((x >> i) & 1) printf ("1");
            else printf ("0");
        }
        printf ("\n");
    }

    // 取出 [l,r] 的块
    int get (int l, int r) {
        if (bel[l] == bel[r]) return b[bel[l]];
        int delta = R[bel[l]] - l + 1;
        return ((b[bel[r]] << delta) | (b[bel[l]] >> (B - delta))) & (S - 1);
    }
    void solve () {
        cin >> n >> m;
        for (int i = 1; i <= n; i ++) {
            char ch;
            cin >> ch;
            a[i] = ch - '0';
            bel[i] = (i - 1) / B + 1;
        }
        for (int i = 1; i <= bel[n]; i ++) {
            L[i] = B * (i - 1) + 1;
            R[i] = i * B;
        }
        for (int i = 1; i <= n; i ++) {
            b[bel[i]] |= (a[i] << (i - L[bel[i]]));
        }

        // 预处理 pre,suf,val
        for (int i = 0; i < S; i ++) {
            while (pre[i] < B && !((i >> pre[i]) & 1)) pre[i] ++;
            while (suf[i] < B && !((i >> (B - 1 - suf[i])) & 1)) suf[i] ++;
            int cnt = 0;
            for (int j = pre[i]; j <= B - 1 - suf[i]; j ++) {
                if (!((i >> j) & 1)) cnt ++;
                else {
                    val[i] += (cnt + 1) * cnt / 2;
                    cnt = 0;
                }
            }
        }

        for (int i = 1; i <= m; i ++) {
            int op, l, r, k;
            cin >> op;
            if (op == 1) {
                cin >> l >> r;
                if (bel[l] == bel[r]) {
                    int pos = bel[l];
                    for (int j = l; j <= r; j ++) {
                        b[pos] ^= (1 << (j - L[pos]));
                    }
                } else {
                    int lpos = bel[l], rpos = bel[r];
                    for (int j = l; bel[j] == lpos; j ++) {
                        b[lpos] ^= (1 << (j - L[lpos]));
                    }
                    for (int j = r; bel[j] == rpos; j --) {
                        b[rpos] ^= (1 << (j - L[rpos]));
                    }
                    if (lpos + 1 == rpos) continue;
                    tag[lpos + 1] ^= 1;
                    tag[rpos] ^= 1;
                }
            } else {
                cin >> k >> l >> r;
                for (int j = 1; j <= bel[n]; j ++) {
                    tag[j] ^= tag[j - 1];
                    if (tag[j]) b[j] ^= (S - 1);
                }
                fill (tag + 1, tag + bel[n] + 1, 0);
                ll ans = 0, j = 0, cnt = 0;
                for (; j + B - 1 < k; j += B) {
                    int s1 = get (l + j, l + j + B - 1);
                    int s2 = get (r + j, r + j + B - 1);
                    int tmp = s1 ^ s2;
                    if (pre[tmp] == B) cnt += B;
                    else {
                        cnt += pre[tmp];
                        ans += val[tmp] + (cnt + 1) * cnt / 2;
                        cnt = suf[tmp];
                    }
                }
                for (; j < k; j ++) {
                    int s1 = ((b[bel[l + j]] >> (l + j - L[bel[l + j]])) & 1);
                    int s2 = ((b[bel[r + j]] >> (r + j - L[bel[r + j]])) & 1);
                    if (s1 != s2) ans += (cnt + 1) * cnt / 2, cnt = 0;
                    else cnt ++;
                }
                ans += (cnt + 1) * cnt / 2;
                cout << ans << '\n';
            }
        }
    }
}

int main () {

    ios :: sync_with_stdio (0);
    cin.tie (NULL);

    michaele :: solve ();

    return 0;
}