5 ABC413 题解
ABC 413 题解
D
题面
给定一个长度为 \(N\) 的整数序列 \(A=(A_1,A_2,\ldots,A_N)\) 。
保证对于任何 \(i\ (1\le i\le N)\) , \(A_i\) 不为 \(0\) 。
判断是否存在 \(A\) 的一个排列 \(B=(B_1,B_2,\ldots,B_N)\) 使得 \(B\) 形成一个等比数列。
如果存在一个实数 \(r\) 使得 \(S_{i+1}=rS_i\) 对于所有整数 \(1\le i\lt N\) 都成立,那么序列 \(S=(S_1,S_2,\ldots,S_N)\) 就是一个等比数列。
\(-10^9 \le A_i \le 10^9 ,\ 1 \le N \le 2 \times 10^5\)
题解
我一开始的思路是先将整个数组按照绝对值大小排序,然后算出 \(a_1 / a_2\) 的值,也就是题目中的 \(r\) ,然后从第二个开始,向后依次算出 \(a_2 / a_3,a_3 / a_4, \cdots\) ,比较他们和 \(r\) 的关系,然后判断是否是一个等比数列,但这样做有两个问题
- 浮点数精度损失,不能够保证正确性
- 可能会出现绝对值相等的情况,也就是说应该是 \(-+-\) 的情况,结果排序过后变成了 \(--+\)
所以我们分别处理这两个问题
- 浮点数有精度损失,我们就将浮点数运算转化为整数运算,因为满足条件的额序列呈等比数列,也就是 \(x,rx,r^2x,r^3x\) 所以我们可以对于 \(3 \le i \le n\) 的每一项 \(a_i\) 验证它是否和前面两项构成等比数列,也就是验证 \(a_{i - 2}a_{i} = a_{i - 1}^2\)
- 我们对每种情况进行分类讨论,然后将他们按照每种情况排列在原数组中,然后利用上面的方法验证
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <map>
#include <cmath>
#include <vector>
using namespace std;
namespace michaele {
typedef long long ll;
typedef __int128 i8;
const int N = 2e5 + 10;
const double eps = 1e-10;
int T, n;
int a[N];
bool cmp (int a, int b) {
return abs (a) < abs (b);
}
void solve () {
vector <int> v0, v1;
int cnt0 = 0, cnt1 = 0;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
if (a[i] < 0) cnt0++, v0.push_back (a[i]);
else cnt1++, v1.push_back (a[i]);
}
if (cnt0 && cnt1) {
if (abs (cnt0 - cnt1) >= 2) {
printf ("No\n");
return;
}
}
sort (v0.begin(), v0.end(), cmp);
sort (v1.begin(), v1.end(), cmp);
bool fn = 1, ans = 0;
//对每种情况进行讨论,排列在原数组中,然后进行验证
if (cnt0 == 0 || cnt1 == 0) {
fn = 1;
sort (a + 1, a + 1 + n, cmp);
for (int i = 3; i <= n; i++) {
if ((ll)a[i - 2] * a[i] != (ll) a[i - 1] * a[i - 1]) {
fn = 0;
break;
}
}
ans |= fn;
} else if (cnt0 == cnt1) {
fn = 1;
int p0 = 0, p1 = 0;
for (int i = 1; i <= n; i += 2) {
a[i] = v0[p0++];
a[i + 1] = v1[p1++];
}
for (int i = 3; i <= n; i++) {
if ((ll)a[i - 2] * a[i] != (ll) a[i - 1] * a[i - 1]) {
fn = 0;
break;
}
}
ans |= fn;
fn = 1;
p0 = 0, p1 = 0;
for (int i = 1; i <= n; i += 2) {
a[i + 1] = v0[p0++];
a[i] = v1[p1++];
}
for (int i = 3; i <= n; i++) {
if ((ll)a[i - 2] * a[i] != (ll) a[i - 1] * a[i - 1]) {
fn = 0;
break;
}
}
ans |= fn;
} else if (cnt0 > cnt1) {
fn = 1;
int p0 = 0, p1 = 0;
for (int i = 1; i <= n; i += 2) {
a[i] = v0[p0++];
}
for (int i = 2; i <= n; i += 2) {
a[i] = v1[p1++];
}
for (int i = 3; i <= n; i++) {
if ((ll)a[i - 2] * a[i] != (ll) a[i - 1] * a[i - 1]) {
fn = 0;
break;
}
}
ans |= fn;
} else {
fn = 1;
int p0 = 0, p1 = 0;
for (int i = 1; i <= n; i += 2) {
a[i] = v1[p1++];
}
for (int i = 2; i <= n; i += 2) {
a[i] = v0[p0++];
}
for (int i = 3; i <= n; i++) {
if ((ll)a[i - 2] * a[i] != (ll) a[i - 1] * a[i - 1]) {
fn = 0;
break;
}
}
ans |= fn;
}
if (ans) printf ("Yes\n");
else printf ("No\n");
}
void main () {
cin >> T;
while (T--) {
solve ();
}
}
}
int main () {
michaele :: main ();
return 0;
}
E
题面
给定一个长度为 \(2^n\) 的排列,编号为 \(0 \sim 2^n - 1\) ,我们可以进行如下操作若干次
- 选定一个起点编号为 \(a \times 2^b\) ,终点编号为 \((a + 1) \times 2^b - 1\) 的区间,然后将区间内的数翻转(\(reverse\)),\(a,b\) 都为非负整数
求任意次操作后字典序最小的排列
\(1 \le n \le 18\)
题解

可以发现,题目要求的就是我们对上面这些区间进行 \(reverse\) 或不操作,最后得到的字典序最小
对于同一层的每个区间,我们发现它们是独立的,也就是他们的元素不发生交换
也就是说对于一个大区间,我们可以分别找到小区间的最优解,然后合并两个小区间,得到大区间的最优解
考虑两个小区间字典序最小的排列分别为 \(a_0, a_1,\cdots\) ,\(b_0,b_1,\cdots\)
- 如果 \(a_0 < b_0\) 那么现在的状态合并起来就还是大区间的最优解
- 如果 \(a0 > b_0\) 那么显然将 \(b_0\) 放在前面, \(a_0\) 放在后面更优,但是又不能直接 \(reverse\) ,所以我们可以反悔一下之前的所有操作,将两个小区间变成 \(\cdots,a_1,a_0\) ,\(\cdots, b_1,b_0\) ,然后再 \(reverse\) ,这样就实现了 \(b_0\) 在前面 \(a_0\) 在后面的操作
所以我们从小到大考虑每个区间,将区间分成左右两个区间,比较左右两个区间的第一个元素,看是否需要交换两个区间,这样就得到了最后的最小字典序
时间复杂度 \(O(n\log n)\)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
using namespace std;
namespace michaele {
const int N = (1 << 18) + 7;
int T, n;
int a[N];
void solve (int l, int r) {
if (l == r) return;
int mid = l + r >> 1;
solve (l, mid), solve (mid + 1, r);
if (a[l] > a[mid + 1]) {
for (int i = l; i <= mid; i++) {
swap (a[i], a[mid + i - l + 1]);
}
}
return;
}
void main () {
cin >> T;
while (T--) {
cin >> n;
for (int i = 0; i < (1 << n); i++) scanf ("%d", &a[i]);
solve (0, (1 << n) - 1);
for (int i = 0; i < (1 << n); i++) printf ("%d ", a[i]);
printf ("\n");
}
}
}
int main () {
michaele :: main ();
return 0;
}
F
题面
有一个 \(H \times W\) 网格。让 \((i,j)\) 表示从上往下第 \(i\) 行,从左往上第 \(j\) 列的单元格。其中, \(K\) 个单元格是目标。目标 \((1 \leq i \leq K)\) 的第 \(i\) 个单元格是 \((R_i, C_i)\) 。
小L 和 小Y 对一个棋子。反复执行以下一系列操作,直到棋子到达目标单元格:
- 小Y 禁止小L 选择四个方向中的一个。
- 然后,小L 在 剩下的四个方向中选择一个方向移动棋子,如果棋子的下一步超出网格边界,则不进行移动
小L 的目标是用尽可能少的步数到达目标点。小Y 的目标是阻止棋子到达目标;如果这不可能,她的目标就是最大限度地增加棋子到达目标的步数。
对于满足 \(1 \leq i \leq H,1 \leq j \leq W\) 的所有点 \((i,j)\) ,求解下面的问题并找出所有解的和:
开始下棋时,棋子位于 \((i,j)\) 小格。假设两位棋手都朝着各自的目标采取最优行动。如果 小L 能够使棋子到达目标,那么解就是最少的步数;否则,解就是 \(0\) 。
\(2 \le H,W \le 3000, 1 \le K \le min (HW, 3000)\)
题解
这道题不同于普通的搜索题,他的核心在于 小Y 会禁掉 小L 的最优决策
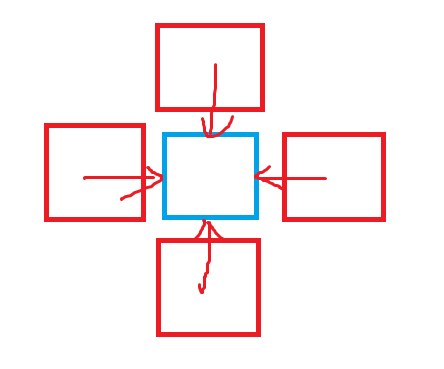
设 \(dis(x,y)\) 表示 \((x, y)\) 到达目标点的最小步数
考虑上图中的蓝色块,假设它由周围的红色块转移过来,那么它一定是被红色点中的次小值更新,而不是最小值,因为 小Y 会禁掉最小值的路径
所以也就相当于我们以所有目标点为起点,去更新其他点,并且我们只在这个点被第二次访问的时候更新它,并放入队列,其实相当于我们求了一条从多个起点到每个点的次短路,我们可以记录一个 \(vis\) 数组表示这个点被访问了多少次,那么我们只会在 \(vis[x] = 2\) 的时候更新它的 \(dis\) 并放入队列
时间复杂度 \(O(nm)\)
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
namespace michaele {
typedef long long ll;
const int N = 3e3 + 10;
int n, m, k;
int vis[N][N], dis[N][N];
int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, 1, -1};
ll sum = 0;
void bfs () {
memset (dis, 0x3f, sizeof dis);
queue <pair <int, int> > q;
for (int i = 1; i <= k; i++) {
int x, y;
cin >> x >> y;
q.push ({x, y});
dis[x][y] = 0;
vis[x][y] = 1;
}
while (q.size ()) {
int x = q.front ().first;
int y = q.front ().second;
q.pop ();
for (int i = 0; i < 4; i++) {
int tx = x + dx[i];
int ty = y + dy[i];
if (tx < 1 || tx > n || ty < 1 || ty > m) continue;
if (!dis[tx][ty]) continue;
vis[tx][ty]++;
if (vis[tx][ty] == 2) {
dis[tx][ty] = dis[x][y] + 1;
q.push ({tx, ty});
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
sum += (dis[i][j] == 0x3f3f3f3f ? 0 : dis[i][j]);
// printf ("%d %d %d\n", i, j, dis[i][j]);
}
}
cout << sum << endl;
}
void main () {
cin >> n >> m >> k;
bfs ();
}
}
int main () {
michaele :: main ();
return 0;
}
G
题面
给定一个 \(n \times m\) 的矩阵,以及 \(k\) 个障碍的坐标 \(r_i,c_i\) ,问从左上角能否走到右下角?
每次移动只能向上下左右四个方向移动
\(1 \le n, m \le 2 \times 10^5, 0 \le k \le 2 \times 10^5\)
题解
因为这道题的 \(n, m\) 巨大,所以我们无法用正常的搜索去解决这道题,只能换个角度去考虑
如果我们无法从左上角走到右下角,那么障碍一定是形如下图的

也就是说障碍一定是联通上右和左下边界的,所以我们可以维护一个并查集,然后将联通的两个点合并,注意这里是八联通
然后对左下的点所在的并查集打个 \(tag\) ,再枚举右上边界的障碍所在的并查集,看是否有 \(tag\) 即可
时间复杂度 \(O(k\log k)\)
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <map>
using namespace std;
namespace michaele {
typedef long long ll;
const int N = 2e5 + 10;
int n, m, k;
int fa[N], tag[N];
map <pair <int, int>, int> mp;
pair <int, int> a[N];
int dx[] = {-1, 1, 0, 0, -1, -1, 1, 1};
int dy[] = {0, 0, 1, -1, 1, -1, 1, -1};
int fin (int x) {
return fa[x] == x ? x : fa[x] = fin (fa[x]);
}
void merge (int x, int y) {
x = fin (x);
y = fin (y);
if (x == y) return;
fa[x] = y;
}
void main () {
cin >> n >> m >> k;
int x, y;
for (int i = 1; i <= k; i++) {
scanf ("%d%d", &x, &y);
mp[{x, y}] = i;
a[i] = {x, y};
}
for (int i = 1; i <= k; i++) fa[i] = i;
for (int i = 1; i <= k; i++) {
x = a[i].first, y = a[i].second;
for (int j = 0; j < 8; j++) {
int tx = x + dx[j], ty = y + dy[j];
if (mp.count ({tx, ty})) {
merge (i, mp[{tx, ty}]);
}
}
}
for (int i = 1; i <= k; i++) {
x = a[i].first, y = a[i].second;
if (x == n || y == 1) {
tag[fin (mp[{x, y}])] = 1;
}
}
bool fn = 0;
for (int i = 1; i <= k; i++) {
x = a[i].first, y = a[i].second;
if (x == 1 || y == m) {
if (tag[fin (mp[{x, y}])]) {
fn = 1;
break;
}
}
}
if (fn) printf ("No\n");
else printf ("Yes\n");
}
}
int main () {
michaele :: main ();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号