24 LCA模拟赛2T4 colorful 题解

Colorful Rectangle

题面

给定 \(n\) 个点，每个点有颜色 \(\in \{0, 1, 2\}\) ，求至少包含三种颜色并且与坐标轴平行的矩形的最小周长。

\(3 \le n \le 10^5\)

\(0 \le x_i , y_i \le 10^8\)

题解

这道题思路不难懂，代码中有个细节卡了我一天。

我们的目标是找到一个矩形至少包含这三种颜色的点，所以这三个点一定限制住了矩形的边界，所以朴素做法就是暴力枚举三个点，然后算周长。

在纸上画一下可以发现矩形的情况大致分为这两大类：

一种是单调的，一种不单调。

那么其他情况呢？其实都可以转化为这两种情况，通过旋转（只是对称变换是无法让所有情况都转化为一种情况的）。

但是对于这三个点的颜色情况还是不确定的，我们可以枚举 6 种排列，然后对每种情况分别统计。

然后考虑这两类情况应该如何统计？

第一种比较简单，可以用树状数组正着反着分别跑一遍，然后枚举中间的那个点统计答案即可。

还有一种比较巧妙的实现：维护两个树状数组，\(T1,T2\)。设 \(pos\) 表示当前点纵坐标离散化后的值。

分情况讨论每个点：

前点直接将 \(-x-y\) 加入 \(T1\)。

中点出现时，在 \(T1\) 中查询 \(pos\) 前缀最小值，然后将这个值加入第二个树状数组的 \(pos\) 位置。

后点的话，在 \(T2\) 中查询 \(pos\) 前缀最小值然后加上当前的 \(x + y\) 更新答案。

第二种情况就要麻烦一点，可以这样做，从小到大枚举每个点，如果是前两个点，我们在 \(y\) 方向区间修改，然后第三个点的时候单点查询，如下图：

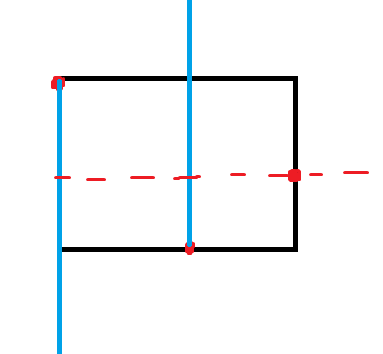
注意：这里的前面两个点不能混在一起算，标记下传的时候如果是中点，要保证只和前面的前点算答案。

时间复杂度 \(O(24 \times n \log n)\)

code

具体看代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

namespace michaele {

    typedef long long ll;

    #define ls (p << 1)
    #define rs (p << 1 | 1)

    const int N = 1e5 + 10;
    const int inf = 0x3f3f3f3f;

    int n;
    int ans = 2e9;
    int b[N], cnt, per[3];
    struct P {
        int x, y, c;
        bool operator < (const P &t) const {
            if (x == t.x) return y < t.y;
            return x < t.x;
        }
    } a[N];

    template <typename T>
    void _min (T &a, T b) { a = min (a, b); }

    struct Fenwick {
        int t[N];
        void clear () { memset (t, 0x3f, sizeof t); }
        void change (int x, int d) {
            while (x < N) {
                _min (t[x], d);
                x += x & -x;
            }
        }
        int ask (int x) {
            int res = 2e9;
            while (x) {
                _min (res, t[x]);
                x -= x & -x;
            }
            return res;
        }

    } T1, T2;

    
    int mn[N << 2][2], val[N << 2];
    
    void pushtag (int p, int v0, int v1) {
        _min (val[p], mn[p][0] + v1);
        _min (mn[p][0], v0);
        _min (mn[p][1], v1);
    }

    void pushdown (int p) {
        pushtag (ls, mn[p][0], mn[p][1]);
        pushtag (rs, mn[p][0], mn[p][1]);
        
        // 保证mn[p][1] 不会和下传下去的 mn[p][0] 组合产生贡献
        mn[p][1] = inf;
    }

    void modify (int p, int l, int r, int x, int y, int v0, int v1) {
        if (x <= l && r <= y) return pushtag (p, v0, v1);
        pushdown (p);
        int mid = (l + r) >> 1;
        if (x <= mid) modify (ls, l, mid, x, y, v0, v1);
        if (mid < y) modify (rs, mid + 1, r, x, y, v0, v1);
    }
    int query (int p, int l, int r, int pos) {
        if (l == r) return val[p];
        pushdown (p);
        int mid = (l + r) >> 1;
        if (pos <= mid) return min (val[p], query (ls, l, mid, pos));
        return min (val[p], query (rs, mid + 1, r, pos));
    }

    void solve () {

        T1.clear ();
        T2.clear ();
        memset (mn, 0x3f, sizeof mn);
        memset (val, 0x3f, sizeof val);

        for (int i = 1; i <= n; i ++) {
            int x = a[i].x, y = a[i].y, c = a[i].c;
            int pos = lower_bound (b + 1, b + 1 + cnt, y) - b;

            // 单调
            if (c == per[0]) T1.change (pos, -x - y);
            else if (c == per[1]) T2.change (pos, T1.ask (pos));
            else {
                _min (ans, x + y + T2.ask (pos));
            }

            // 不单调
            if (c == per[0]) {
                modify (1, 1, cnt, pos, cnt, -x - y, inf);
            } else if (c == per[1]) {
                modify (1, 1, cnt, 1, pos, inf, y);
            } else if (c == per[2]) {
                _min (ans, query (1, 1, cnt, pos) + x);
            }
        }
    }

    void Main () {
        cin >> n;
        for (int i = 1; i <= n; i ++) {
            cin >> a[i].x >> a[i].y >> a[i].c;
        }

        for (int k = 0; k < 4; k ++) {
            per[0] = 0, per[1] = 1, per[2] = 2;
            cnt = 0;
            for (int i = 1; i <= n; i ++) {
                b [ ++ cnt] = a[i].y;
            }
            sort (a + 1, a + 1 + n);
            sort (b + 1, b + 1 + cnt);
            cnt = unique (b + 1, b + 1 + cnt) - 1 - b; 
            do {
                solve ();
            } while (next_permutation (per, per + 3));
            for (int i = 1; i <= n; i ++) {
                swap (a[i].x, a[i].y);
                a[i].y *= -1;
            }
        }

        cout << (ans << 1) << endl;
    }
}

int main () {

    michaele :: Main ();


    return 0;
}