18 LCA模拟赛1T3 旅行vacation 题解

旅行vacation

题面

给定 \(n\) 个区间对应的 \(L_i, R_i\) ，每个点代表一个单位长度

给定 \(K\) 表示可以移动区间共 \(K\) 个单位长度，每个区间可以向左也可以向右

求最多有多少个单位长度能被覆盖 \(n\) 次

\(1 \le n \le 5 \times 10^5\)

\(1 \le L_i \le R_i \le 10^9,\ 0 \le K \le 10^{18}\)

题解

首先，最终被覆盖 \(n\) 次的这些单位长度一定构成一个连续的区间

那么这个区间长度显然是有单调性的，如果一个区间长度满足条件，那么对于一个更短的区间长度一定也是满足条件的

所以我们可以尝试二分一个区间长度，使区间长度尽可能长

问题在于我们如何快速判断一个区间长度是否可行，这里我们用两个函数来帮助我们截距这个问题

设当前二分的区间长度为 \(len\)，\(f(x)\) 表示覆盖以 \(x\) 为左端点长度为 \(len\) 的固定区间的最小移动距离，\(g_i(x)\) 表示第 \(i\) 个区间覆盖固定区间的最小移动距离，有 \(f(x) = \sum g_i(x)\)

\(g_i(x)\) 的函数方程不难推出

\[\begin{align*} g_i(x) = \begin{cases} L_i - x, &x < L_i \\ 0, &L_i \le x \le R_i - len + 1 \\ x + len - 1 - R_i, &R_i < x + len - 1 \end{cases} \end{align*} \]

这实际上是一个下凸的分段函数，将函数图像画出来

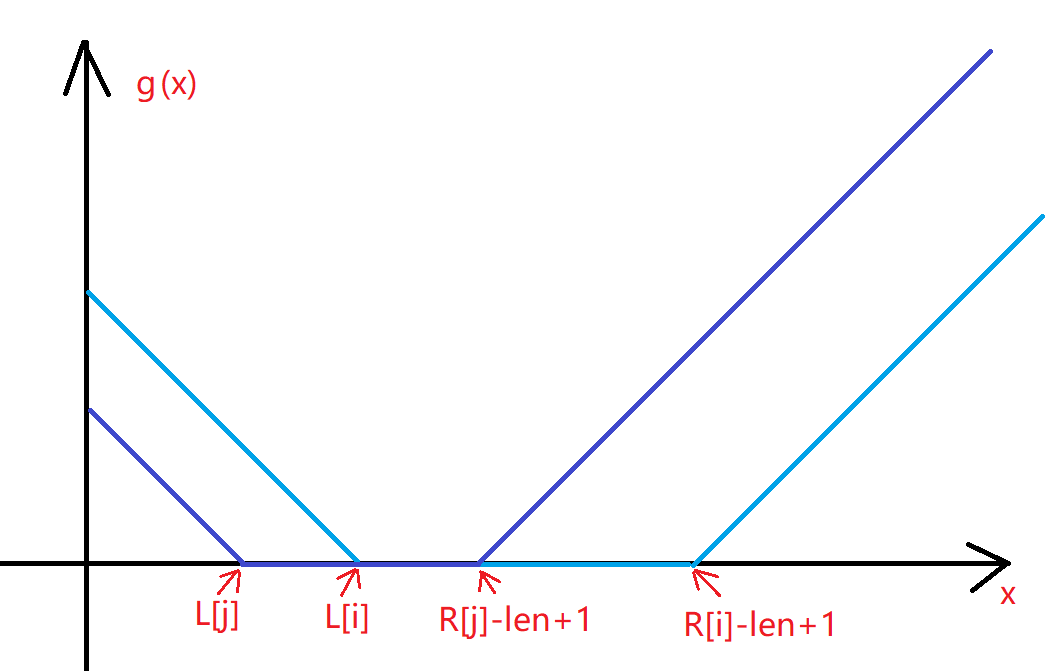
根据这个图像，我们可以再将 \(f(x)\) 的图像画出来（先只看 \(g_i,g_j\)）

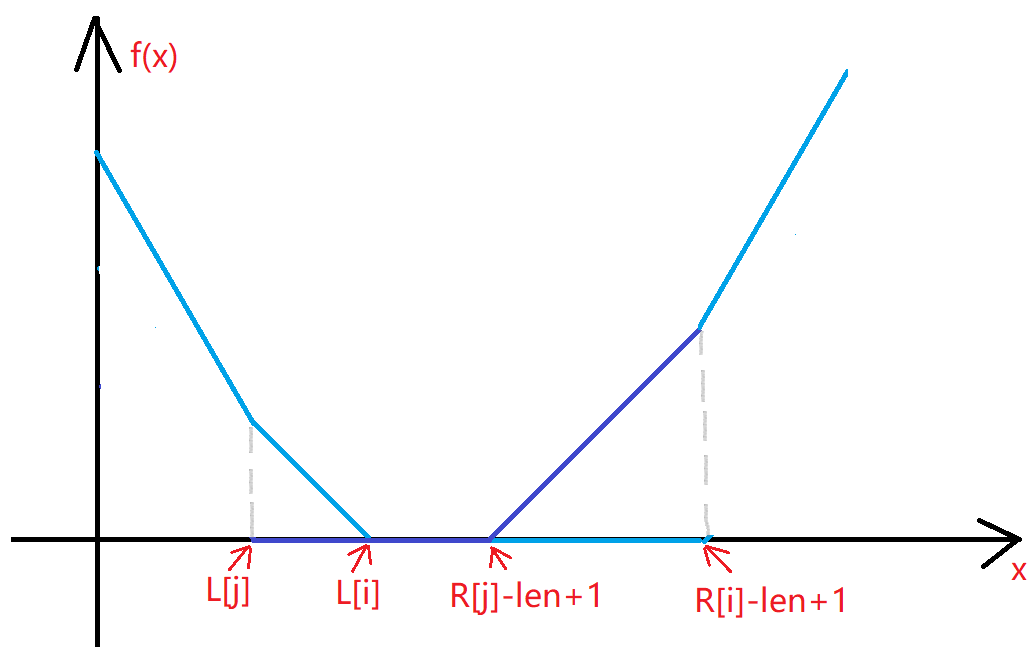
根据凸函数加凸函数还是凸函数的性质，我们的 \(f(x)\) 也一定是下凸的

因为我们要取最小值，所以我们枚举左端点 \(x\) 的时候只考虑这些折点即可，这样就能避免 \(10^9\) 枚举左端点了

但是即便是枚举这些折点，然后再去枚举每个区间，时间复杂度是 \(O(n^2)\) 的

考虑 \(f(x)\) 的构成，其实可以写成这样的式子

\[f(x) = \sum_{i = 1}^n (L_i - x)[x < L_i] + (x + len - 1 - R_i)[x + len - 1 > R_i] \]

发现对于每个区间 \(L_i, R_i\) 对 \(f(x)\) 的贡献是独立的，所以我们可以分别将 \(L_i,R_i\) 排序

对于每个 \(x\) ，我们都可以二分出最小的 \(L_i\) 使得 \(x < L_i\) 的位置 \(p1\) ，最大的 \(R_i\) 使得 \(x + len - 1 > R_i\) 的位置 \(p2\)

答案即为：$suml_n - suml_{p1} - x \times p1 + (x + len - 1) \times p2 - sumr_{p2} $

但是如果套两个二分，时间复杂度是有点高的，会TLE

再仔细观察，实际上我们可以不用二分 \(p1,p2\) ，这两个指针实际上都会随着 \(x\) 增大而递增

所以我们直接维护这两个指针，这样就能在 \(O(n)\) 的时间复杂度内 \(check\)

总时间复杂度 \(O(n \log V)\) 其中 \(V\) 是值域

code

namespace solution_c {

    const int N = 5e5 + 10;

    int n;
    ll K;
    int L[N], R[N];
    ll suml[N], sumr[N];

    bool check (int len) {
        int p1 = 1, p2 = 0;
        for (int i = 1; i <= n; i ++) {
            ll res = 0, x = L[i];
            while (p1 <= n && x >= L[p1]) p1 ++;
            while (p2 + 1 <= n && R[p2 + 1] <= x + len - 1) p2 ++;
            res += suml[n] - suml[p1 - 1] - (ll)(n - p1 + 1) * x;
            res += (ll)(x + len - 1) * p2 - sumr[p2];
            if (res <= K) return true;
        }
        
        p1 = 1, p2 = 0;
        for (int i = 1; i <= n; i ++) {
            ll res = 0, x = R[i] - len + 1;
            while (p1 <= n && x >= L[p1]) p1 ++;
            while (p2 + 1 <= n && R[p2 + 1] <= x + len - 1) p2 ++;            
            res += suml[n] - suml[p1 - 1] - (ll)(n - p1 + 1) * x;
            res += (ll)(x + len - 1) * p2 - sumr[p2];
            if (res <= K) return true;
        }
        return false;
    }

    void solve () {
        // close_stream ();

        cin >> n >> K;
        int mn = 2e9;
        for (int i = 1; i <= n; i ++) {
            cin >> L[i] >> R[i];
            mn = min (mn, R[i] - L[i] + 1);
        }
        sort (L + 1, L + 1 + n);
        sort (R + 1, R + 1 + n);

        for (int i = 1; i <= n; i ++) {
            suml[i] = suml[i - 1] + L[i];
            sumr[i] = sumr[i - 1] + R[i];
        }

        int l = 0, r = mn;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (check (mid)) l = mid;
            else r = mid - 1;
        }
        cout << l << endl;
    }
}