1 ABC404 A~E 题解
A
题面
给你一个长度介于 \(1\sim25\) 之间的字符串 \(S\) ,它由小写英文字母组成。
请输出一个没有出现在 \(S\) 中的小写英文字母。如果有多个,输出其中任意一个即可。
题解
直接用一个 \(vis[]\) 记录每个字母是否出现过即可
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cstdio>
using namespace std;
namespace michaele {
int n;
bool vis[26];
void main () {
string s;
cin >> s;
for (int i = 0; i < (int)s.size(); i++)
vis[s[i] - 'a' + 1] = 1;
for (int i = 1; i <= 26; i++) {
if (!vis[i]) {
printf ("%c", i + 'a' - 1);
break;
}
}
return;
}
}
int main () {
michaele :: main ();
return 0;
}
B
题面
有两个网格 \(S\) 和 \(T\) ,每个网格有 \(N\) 行和 \(N\) 列。让 \((i,j)\) 表示从上往下数第 \(i\) 行和从左往上数第 \(j\) 列的单元格。
网格 \(S\) 和 \(T\) 中的每个单元格都被涂成白色或黑色。如果 \(S_{i,j}\) 为".",则 \(S\) 的 \((i,j)\) 单元格为白色;如果 \(S_{i,j}\) 为 "#",则 \((i,j)\) 单元格为黑色。同样的情况也适用于 \(T\) 。
您可以按任意顺序执行以下两种类型的运算任意多次。求使网格 \(S\) 与网格 \(T\) 相同所需的最少运算次数。
- 选择网格 \(S\) 中的一个单元格并改变其颜色。
- 将整个网格 \(S\) 顺时针旋转 \(90\) 度。
\(1 \leq N \leq 100\)
题解
这题当时想了想,不太知道怎么优雅的做出来,后来直接暴力模拟了,看题解好像代码比较优雅,但思路差不多
如果不再旋转,那么当前 \(S\) 与 \(T\) 中不同的方格的数量就是答案
如果旋转,那我们需要知道旋转后的每个点的坐标
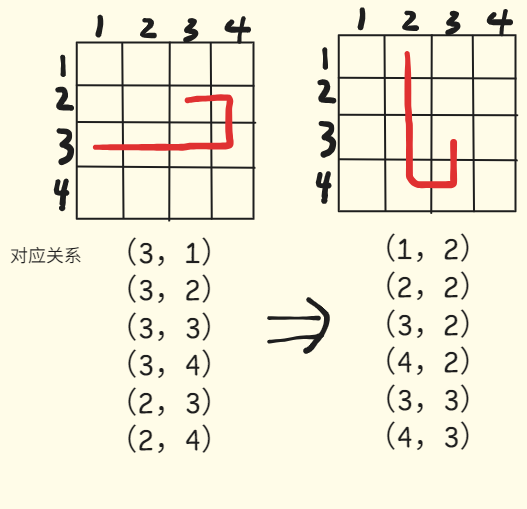
不难发现,原本的 \((x,y)\) 变成 \((y,n+1-x)\) ,这样我们就可以实现旋转操作
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cstdio>
using namespace std;
namespace wjl {
const int N = 110;
int n;
int a[N][N][4];
int b[N][N];
char s[110];
void main () {
scanf ("%d", &n);
for (int i = 1; i <= n; i++) {
scanf ("%s", s + 1);
for (int j = 1; j <= n; j++) {
a[i][j][0] = s[j] == '.' ? 0 : 1;
}
}
for (int i = 1; i <= n; i++) {
scanf ("%s", s + 1);
for (int j = 1; j <= n; j++) {
b[i][j] = s[j] == '.' ? 0 : 1;
}
}
for (int t = 1; t <= 3; t++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
a[j][n + 1 - i][t] = a[i][j][t - 1];
}
}
}
int ans[4] = {0, 1, 2, 3};
for (int t = 0; t <= 3; t++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][j][t] != b[i][j]) {
ans[t]++;
}
}
}
}
sort (ans, ans + 4);
printf ("%d\n", ans[0]);
return;
}
}
int main () {
wjl :: main ();
return 0;
}
C
题面
给你一个简单的无向图,图中有 \(N\) 个顶点和 \(M\) 条边。顶点编号为 \(1,2,\dots,N\) ,边编号为 \(1,2,\dots,M\) 。边 \(i\) 连接顶点 \(A _{i}\) 和 \(B _{i}\) 。(不存在重边和自环)
循环图的定义 如果存在 \((1,2,\dots,N)\) 的 \((v_{1},v_{2}\dots ,v_{N})\) 排列,且顶点标记为 \(1,2,\dots,N\) ,则 \(N\) 顶点图是循环图:
- 对于每个 \(i = 1,2,\dots,N-1\) ,顶点 \(v_{i}\) 和 \(v_{i+1}\) 之间有一条边。
- 顶点 \(v _{N}\) 与 \(v _{1}\) 之间有一条边。
- 不存在其他边。
请判断该图是否为循环图。
- \(3 \le N \le 2\times 10^5\)
- \(0 \le M \le 2\times 10^5\)
- \(1 \le A_i, B_i \le N\)
题解
判断是否满足以下条件
- \(n\) 个点 \(n\) 条边
- 每个点连 \(2\) 条边
- 整个图联通(可用DFS或并查集)
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
using namespace std;
namespace michaele {
const int N = 2e5 + 10;
int n, m;
vector <vector<int>> e(N);
bool vis[N];
bool ok = 1;
void dfs (int x, int fa) {
if (vis[x]) return;
vis[x] = 1;
if ((int)e[x].size() != 2) {
ok = 0;
return;
}
for (auto y : e[x]) {
if (y == fa) continue;
dfs (y, x);
}
}
void main () {
scanf ("%d%d", &n, &m);
if (n != m) {
printf ("No\n");
return;
}
int x, y;
for (int i = 1; i <= m; i++) {
scanf ("%d%d", &x, &y);
e[x].push_back (y);
e[y].push_back (x);
if ((int)e[x].size() > 2 || (int)e[y].size() > 2) {
printf ("No\n");
return;
}
}
dfs (1, 0);
if (!ok) {
printf ("No\n");
return;
}
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
printf ("No\n");
return;
}
}
printf ("Yes\n");
return;
}
}
int main () {
michaele :: main ();
return 0;
}
D
题面
\(AT\) 国家有 \(N\) 个动物园,编号为 \(1\) 至 \(N\) 。动物园 \(i\) 的门票是 \(C_i\) 元。
小乐喜欢 \(M\) 种动物,动物 \(1,\dots,M\) 。
动物园 \(K_i\) ,即动物园 \(A_{i,1},\dots,A_{i,K_i}\) 可以看到动物 \(i\) 。
求观看所有 \(M\) 种动物每种至少两次最少多少钱。
如果多次游览同一动物园,则每次游览都被视为观赏一次动物。
- \(1 \le N \le 10\)
- \(1 \le M \le 100\)
题解
对于每个动物园来说,小乐最多去两次,因为第三次对答案没有任何贡献
又因为 \(1 \leq N \leq 10\) ,所以我们可以直接暴搜,枚举每个动物园去 \(0,1,2\) 次
时间复杂度 \(O(3^{N}NM)\)
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
using namespace std;
namespace michaele {
typedef long long ll;
const int N = 110;
int n, m;
vector <vector<int>> e(N);
ll c[N], ans = 2e18;
int ct[N];
//i 表示当前所处的动物园, cost代表到现在要花多少钱
void dfs (int i, ll cost) {
if (i > n) {
for (int j = 1; j <= m; j++) {
if (ct[j] < 2) return;
}
ans = min (ans, cost);
return;
}
//不看
dfs (i + 1, cost);
//看一次
for (auto j : e[i]) ct[j]++;
dfs (i + 1, cost + c[i]);
for (auto j : e[i]) ct[j]--;
//看两次
for (auto j : e[i]) ct[j] += 2;
dfs (i + 1, cost + c[i] * 2);
for (auto j : e[i]) ct[j] -= 2;
}
void main () {
scanf ("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf ("%lld", &c[i]);
for (int i = 1; i <= m; i++) {
int x;
scanf ("%d", &x);
for (int j = 1; j <= x; j++) {
int xx;
scanf ("%d", &xx);
e[xx].push_back (i);
}
}
dfs (1, 0);
printf ("%lld\n", ans);
return;
}
}
int main () {
michaele :: main ();
return 0;
}
E
题面
有 \(N\) 个碗排成一排,从左到右编号为 \(0,1,\dots,N-1\) 。
每个碗 \(i\) ( \(1\le i\le N-1\) ) 上都写着一个整数 \(C_i\) ,最初碗里有 \(A_i\) 粒豆子。
碗 \(0\) 上没有写任何整数,最初也没有豆子。
下面的操作可以重复任意多次:
- 选择一个碗 \(i\) ( \(1\le i\le N-1\) ),从中取出一颗或多颗豆子。
- 将取出的豆子在碗 \(i-C_i,i-C_i+1,\dots,i-1\) 中自由分配。
- 从形式上看,当你取出 \(k\) 粒豆子时,你必须将总共 \(k\) 粒豆子放入碗 \(i-C_i,i-C_i+1,\dots,i-1\) 中,你可以选择每只碗中放入多少粒豆子。
求将所有豆子放入碗 \(0\) 所需的最少操作次数。
题解
这题要求最小操作次数,考虑不同的操作顺序对答案的影响
- 先动左边,再动右边,那么右边的移动到左边后要额外消耗操作次数
- 先动右边,再动左边,将左边原有的和右边移过来的一起动,即可节省操作次数
那么我们从右到左将每个碗中的豆子都移到更左边的碗中,那么这就是最优的答案
这里用最短路的做法,枚举每个碗
- 从右到左枚举每个可以转移的碗,如果这个碗中有豆子,那么连一条左边到右边的边,退出循环
- 如果没有找到有豆子的碗,那么向每个可转移碗都连一条左边到右边的边
最后以 \(0\) 为起点跑 \(dijkstra\) 即可
最后答案就是最右边的第一个有豆子的碗的 \(d[x]\)
时间复杂度 \(O(N^{2})\) ,瓶颈在建边
code
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
namespace wjl {
const int N = 2e3 + 10;
int n;
int a[N], c[N], d[N];
vector <vector<int>> e (N);
bool vis[N];
void dj (int s) {
memset (d, 0x3f, sizeof d);
priority_queue<pair<int, int>> q;
d[s] = 0;
q.push({0, s});
while (q.size()) {
int x = q.top().second; q.pop();
if (vis[x]) continue;
vis[x] = 1;
for (auto y : e[x]) {
if (d[y] > d[x] + 1) {
d[y] = d[x] + 1;
q.push({-d[y], y});
}
}
}
}
void main () {
scanf ("%d", &n);
for (int i = 1; i < n; i++)
scanf ("%d", &c[i]);
for (int i = 1; i < n; i++)
scanf ("%d", &a[i]);
for (int i = 1; i < n; i++) {
bool fn = 0;
for (int j = i - 1; j >= i - c[i]; j--) {
if (a[j]) {
e[j].push_back (i);
fn = 1;
break;
}
}
if (!fn) {
for (int j = i - c[i]; j <= i - 1; j++)
e[j].push_back (i);
}
}
dj (0);
for (int i = n - 1; i >= 1; i--) {
if (a[i]) {
printf ("%d\n", d[i]);
return ;
}
}
return;
}
}
int main () {
wjl :: main ();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号