6 2025 05 03 模拟赛题解
题面及题解
T1
题面
众所周知,小乐家非常有钱,他家有一个 \(2n \times 2m\) 的矩形水池,被一些宽度不记的隔板隔开,每个 \(2 \times 2\) 的小矩形中都有两块弧形隔板,且只可能是这两种图案中的一种:

这两种图形都由一个边长为 \(2\) 的正方形和两个半径为 \(1\) 的 \(\frac{1}{4}\) 园组成
水池左上角坐标为 \((0,0)\) ,右下角坐标为 \((2n, 2m)\),小乐家的水池都由这两种图案构成,现在,小乐想要在某个坐标点上倒下一桶染料,使得他家的水池五彩缤纷,他想要知道倒在每个坐标的染料最多可以扩展多大面积
(注意,如果倒在了隔板上,扩展面积为0)
如下图,\(n=m=4\) ,左上角坐标为 \((0,0)\) ,右下角坐标为 \((8,8)\) ,同色的部分表示可以可以互相到达的区域
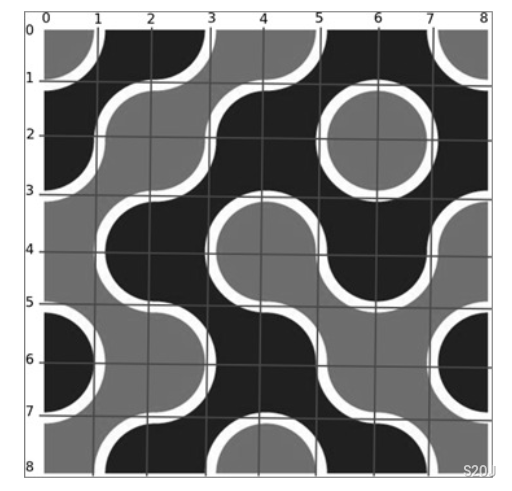
\(1\leq n,\,m,\,q\leq 100\)
\(0 \leq x \leq 2n,\, 0 \leq y \leq 2m\)
题解
直接暴力DFS即可,问题在于如何设计DFS的每个状态,,我在考场上的思路是以每个 \(2 \times 2\) 的方块作为DFS的状态,但不能直接用每个块,因为每个块中又细分为三个部分,它们能够扩展的方向不同,所以要细分为,当前到达了哪个块的哪个部分,如此便可以进行转移了
还有个小问题是如何确定每个 \((x, y)\) 所在块的左边 \(x',y'\)
我们先处理比较特殊的情况,以 \(0\) 块为例
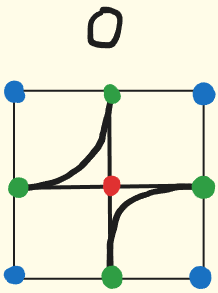
图中红色点在块的中心,所在块的坐标 \((x',y')=( \frac{x}{2}, \frac{y}{2} )\),再看绿色点,它所在的位置即为隔板边缘位置,而它的坐标也很有特点,横纵坐标一奇一偶,所以很好判断。最后再来看蓝色点,这四个点位于一个正方形的四个角上,我们并不好直接确定它们所处块的坐标, 先默认这个点所处块的坐标\((x',y')=\left( \frac{x}{2} , \frac{y}{2} \right)\) ,也就是默认为这个点左上角的块,但是会出现一些问题,就是这个块可能压根不存在,所以我们要对这种情况进行特殊处理,如下图
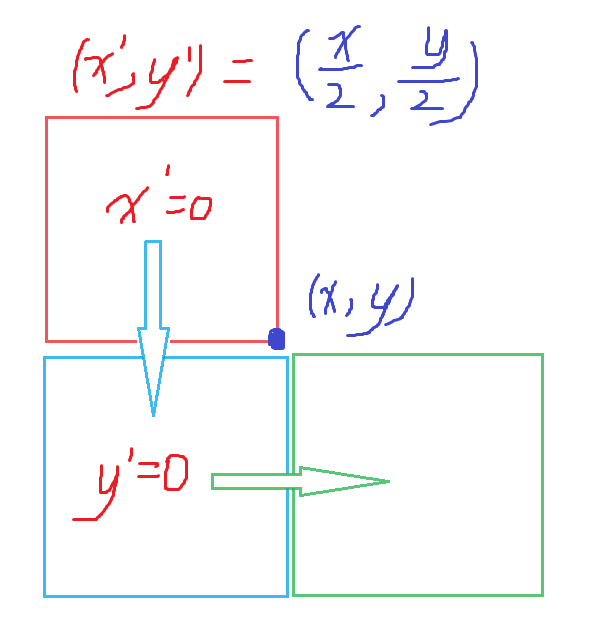
如果 \(x' = 0\) ,说明当前点处于最上面,上面没有块,所以要将原定的块向下移动一位,也就是蓝色箭头的变化
若 \(y'=0\) ,说明当前点处于最左边,将原定块向右移动一位,即绿色箭头的变化
最后我们找到一个合法的坐标进行DFS,这题最恶心的分类讨论就要来了,这个自己推吧,就是在 \(0 / 1\) 块的每个部分,能够向哪里转移,转移后到达新块的哪个部分,给个手画的图,可以作为参考

code
namespace wjl {
const int N = 220;
const double pi = 3.141592653589793;
int n, m, q;
int a[N][N];
//分别对应上右下左
int mx[4] = {-1, 0, 1, 0};
int my[4] = {0, 1, 0, -1};
char s[N];
bool vis[N][N][4];
double dfs (int x, int y, int bel) {
if (vis[x][y][bel]) return 0;
if (x < 1 || x > n || y < 1 || y > m) return 0;
vis[x][y][bel] = 1;
// printf ("%d %d\n", x, y);
double res = 0;
res += bel == 2 ? 4 - pi / 2 : pi / 4;
if (a[x][y] == 0) {
//此块为0
if (bel == 2) {
for (int i = 0; i < 4; i++) {
if (a[x + mx[i]][y + my[i]] == 0) {
if (i == 0) res += dfs (x + mx[i], y + my[i], 3);
else if (i == 1) res += dfs (x + mx[i], y + my[i], 1);
else if (i == 2) res += dfs (x + mx[i], y + my[i], 1);
else if (i == 3) res += dfs (x + mx[i], y + my[i], 3);
} else {
res += dfs (x + mx[i], y + my[i], 2);
}
}
} else {
if (bel == 1) {
res += dfs (x - 1, y, a[x - 1][y] == 0 ? 2 : 1);
res += dfs (x, y - 1, a[x][y - 1] == 0 ? 2 : 3);
} else {
res += dfs (x, y + 1, a[x][y + 1] == 0 ? 2 : 1);
res += dfs (x + 1, y, a[x + 1][y] == 0 ? 2 : 3);
}
}
} else {
//此块为1
if (bel == 2) {
for (int i = 0; i < 4; i++) {
if (a[x + mx[i]][y + my[i]] == 1) {
if (i == 0) res += dfs (x + mx[i], y + my[i], 1);
else if (i == 1) res += dfs (x + mx[i], y + my[i], 1);
else if (i == 2) res += dfs (x + mx[i], y + my[i], 3);
else if (i == 3) res += dfs (x + mx[i], y + my[i], 3);
} else {
//下一块为0
res += dfs (x + mx[i], y + my[i], 2);
}
}
} else {
if (bel == 1) {
res += dfs (x + 1, y, a[x + 1][y] == 1 ? 2 : 1);
res += dfs (x, y - 1, a[x][y - 1] == 1 ? 2 : 3);
} else {
res += dfs (x - 1, y, a[x - 1][y] == 1 ? 2 : 3);
res += dfs (x, y + 1, a[x][y + 1] == 1 ? 2 : 1);
}
}
}
return res;
}
void main () {
scanf ("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf ("%s", s + 1);
for (int j = 1; j <= m; j++) {
a[i][j] = s[j] - '0';
}
}
scanf ("%d", &q);
while (q--) {
memset (vis, 0, sizeof vis);
int x, y;
scanf ("%d%d", &x, &y);
if ((x & 1) != (y & 1)) {
printf ("%.4lf\n", (double)0);
continue;
}
int bel = 0;
if ((x & 1) && (y & 1)) {
x = x / 2 + 1;
y = y / 2 + 1;
bel = 2;
} else {
int fnx = 0, fny = 0;
x /= 2, y /= 2;
if (x <= 0) x += 1, fnx = 1;
if (y <= 0) y += 1, fny = 1;
bel = a[x][y];
//右下
if (!fnx && !fny) {
if (!bel) bel = 3;
else bel = 2;
} else if (fnx && !fny) {
//右上
bel = bel == 0 ? 2 : 3;
} else if (!fnx && fny) {
//左下
bel = bel == 0 ? 2 : 1;
} else if (fnx && fny) {
//左上
bel = bel == 0 ? 1 : 2;
}
}
printf ("%.4lf\n", dfs (x, y, bel));
}
return;
}
}
int main () {
wjl :: main();
return 0;
}
T2
题面
小乐想用程序实现一个功能强大的数列编辑器,可是他不会,所以来问你
一开始数列为空,有下面几种操作
- \(I\ x\) :在光标的后面插入一个数字 \(x\) ,并将光标移到这个新加入的 \(x\) 后。
- \(D\) :删除光标前的最后一个数字(保证存在),光标位置不变。
- \(L\) :光标左移一位,如果已经在开头则不做任何事。
- \(R\) :光标右移一位,如果已经在结尾则不做任何事。
- \(Q\ k\) :编辑器需要给出 \(A_1\ A_2\ \cdots\ A_k\) 的最大前缀和(前缀长度不能为0),保证 \(1\le k\le N\) ,其中 \(N\) 为当前光标前的数字个数。
\(q \leq 10^{6}\) , \(q\) 为操作次数
题解
这题可以用两个栈去维护,一个维护光标左边的数( \(sta\) ),另一个维护光标右边的数( \(stb\) )
- \(I\ x\) : \(sta\) 插入 \(x\),维护 \(f[],s um[]\)
- \(D\) : \(sta\) 删除栈顶
- \(L\) : \(sta\) 压入 \(stb\) 栈顶, \(stb\) 栈顶弹出,维护 \(f[],s um[]\)
- \(R\) : \(stb\) 压入 \(sta\) 栈顶, \(sta\) 栈顶弹出,维护 \(f[],s um[]\)
- \(Q\ k\) :输出 \(f[k]\) 即可
注意处理好空栈的情况
code
namespace wjl {
const int N = 1e6 + 10;
int n;
int sta[N], stb[N], ta, tb;
int f[N], sum[N];
void main () {
memset (f, 0xaf, sizeof f);
scanf ("%d", &n);
char op[10];
int cnt = 0;
ta = 0, tb = 0;
for (int i = 1; i <= n; i++) {
scanf ("%s", op);
if (op[0] == 'I') {
scanf ("%d", &sta[++ta]);
sum[ta] = sum[ta - 1] + sta[ta];
f[ta] = max (f[ta - 1], sum[ta]);
} else if (op[0] == 'D') {
if (ta) ta--;
} else if (op[0] == 'L') {
if (!ta) continue;
stb[++tb] = sta[ta];
ta--;
} else if (op[0] == 'R') {
if (!tb) continue;
sta[++ta] = stb[tb];
sum[ta] = sum[ta - 1] + sta[ta];
f[ta] = max (f[ta - 1], sum[ta]);
tb--;
} else if (op[0] == 'Q') {
int k;
scanf ("%d", &k);
printf ("%d\n", f[k]);
}
}
return;
}
}
int main () {
wjl :: main ();
return 0;
}
T3
不会
T4
题面
企鹅国的网吧们之间由网线互相连接,形成一棵树的结构。由于天太冷,拆一些网线来做燃料。但是现在有 \(k\) 只企鹅要上网游戏,所以他们需要把这 \(k\) 只企鹅安排到不同的机房,但是需要保证每只企鹅至少还能通过留下来的网线和至少另一只企鹅联机游戏。
所以他们想知道,最少需要保留多少根网线?
\(2 \leq k \leq n \leq 10^{5}\)
题解
题中直截了当的给了树形结构,并且问的是最少保留多少网线,做题多的应该能很自然地想到DP(我做题不多,所以没想出来?)
我们要求的是最少的网线数量,也就是用最少的边使 \(k\) 个节点不相互孤立,那么性价比最高的方法就是:一条边的两端分别是两个从未被其他边连过的点
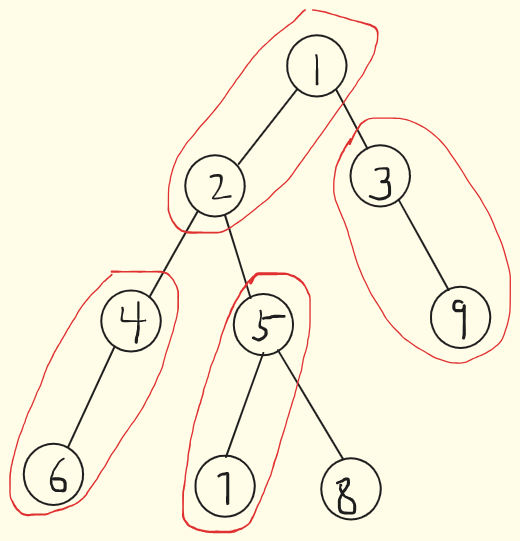
我们在一棵树中求出像这样的点对最多有多少,假设我们已经求出来,记为 \(sum\) (也就是图中红色圈的数量),进行分讨
- \(s u m\times 2\geq k\) ,也就是说这样的点对足够放下 \(k\) 个点 ,那么直接两个点一条边,不够的话再补一条即可, \(ans = (k+1) / 2\)
- \(s um \times 2 < k\) ,这些部分不够放下 \(k\) 个点,需要额外加边,额外加边的数量即为多的点的数量,也就是 \(k - s um \times 2\) ,最终的答案 \(ans = k - s um\)
下面我们说如何DP
设 \(f[x][0 / 1]\) 表示以 \(x\) 节点为根的子树中,包含/不包含 \(x\) 节点
转移方程
这里 \(f[x][0]\) 的转移应该不难理解,我在这里说一下 \(f[x][1]\) 的转移
这里如果 \(f[x][1] = f[x][0] + f[y][0] - f[y][1] + 1\) ,那么相当于 \(x\) 这个节点,与当前的 \(y\) 节点构成一个点对,因此要将 \(y\) 子树中不选 \(y\) 的贡献加上,将选 \(y\) 的贡献减去,再加上新点对的 \(1\) 即可
code
namespace wjl {
const int N = 1e5 + 10;
int t, n, k;
int h[N], ver[N << 1], ne[N << 1], tot;
int f[N][2];
void add (int x, int y) {
ver[++tot] = y;
ne[tot] = h[x];
h[x] = tot;
}
void dfs (int x, int fa) {
for (int i = h[x]; i; i = ne[i]) {
int y = ver[i];
if (y == fa) continue;
dfs (y, x);
f[x][0] += f[y][1];
}
for (int i = h[x]; i; i = ne[i]) {
int y = ver[i];
if (y == fa) continue;
f[x][1] = max (f[x][1], f[x][0] - f[y][1] + f[y][0] + 1);
}
}
void main () {
scanf ("%d", &t);
while (t--) {
memset (f, 0, sizeof f);
scanf ("%d%d", &n, &k);
for (int i = 1; i <= n; i++)
h[i] = 0;
tot = 0;
int x;
for (int i = 2; i <= n; i++) {
scanf ("%d", &x);
add (i, x);
add (x, i);
}
dfs (1 ,0);
int ans = max (f[1][1], f[1][0]);
if (ans * 2 >= k) printf ("%d\n", (k + 1) / 2);
else printf ("%d\n", k - ans);
}
return;
}
}
int main () {
wjl :: main ();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号