结对项目

1.提交

这个作业属于哪个课程	https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience
这个作业要求在哪里	https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/homework/13479
github仓库链接	https://github.com/1610285721-svg/3123004531_jiedui
成员1	梁法恩 3123004531
成员2	纪泓鑫 3123004529

2.PSP表格

Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
估计这个任务需要多少时间	30	40
需求分析 (包括学习新技术)	60	50
生成设计文档	45	50
设计复审 (和同事审核设计文档)	30	30
代码规范 (为目前的开发制定合适的规范)	20	15
具体设计	60	70
具体编码	300	250
代码复审	45	45
测试（自我测试，修改代码，提交修改）	150	180
测试报告	45	45
计算工作量	15	15
事后总结, 并提出过程改进计划	30	20
合计	830	820

3.效能分析
优化花了2小时
起初：
生成速度慢：随机生成表达式后，大量因 “不合法”（如减法为负、除法为假分数）被丢弃。
重复率高：没有去重逻辑导致生成的题目中存在大量等价表达式，实际有效题目数量不足。
计算开销大：表达式计算时频繁进行字符串解析和格式转换，尤其带括号的复杂表达式，重复计算相同子表达式，浪费资源。
改进：
运算符选择优化：若前一个运算符是 “-” 或 “÷”，下一个运算符强制选择 “+” 或 “×”（避免连续减 / 除导致的无效计算）。
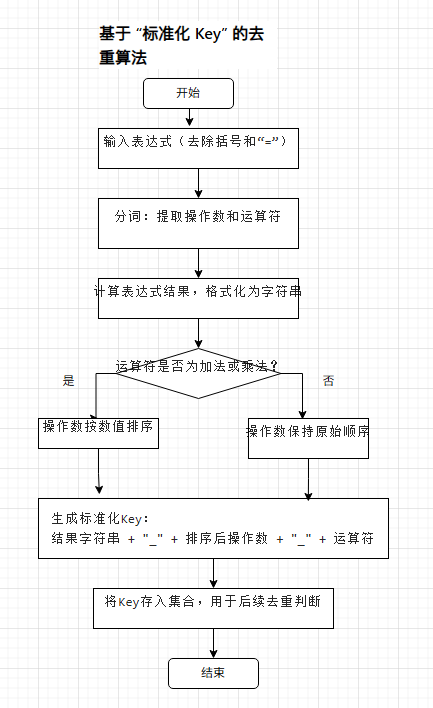
放弃字符串直接比对：设计 “标准化 Key”（结果 + 排序操作数 + 运算符），对加法 / 乘法自动排序操作数。
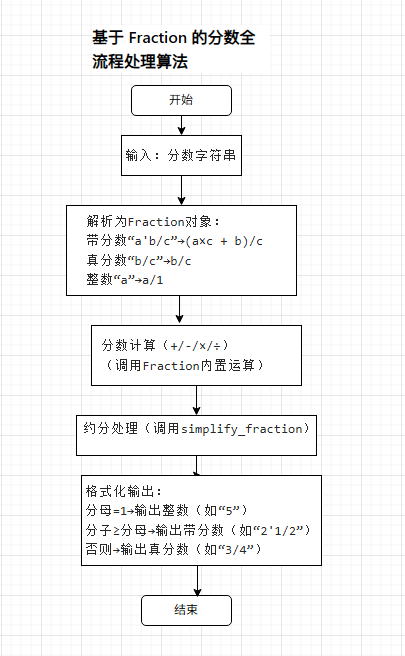
缓存分数解析结果：解析后缓存结果（如用字典存储 “3'1/2”→Fraction(7,2)），重复解析同一分数时直接复用。

生成算式

批改算式

4.设计实现过程
MathExpression 类

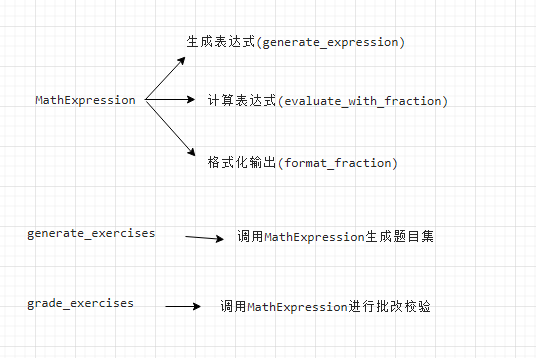
流程图

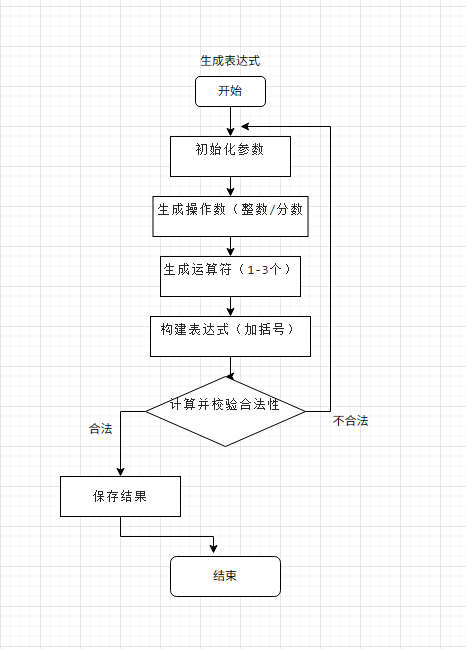
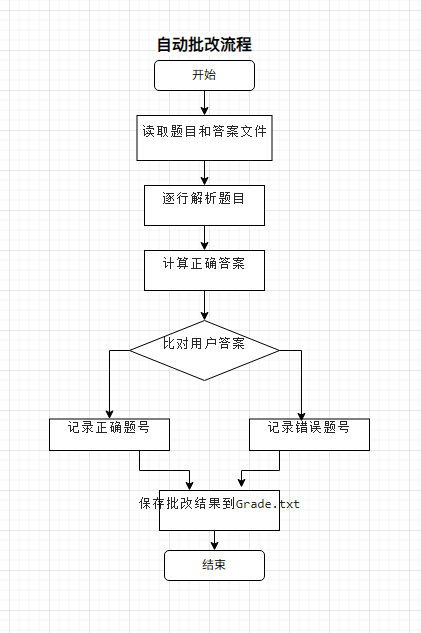
5.关键算法的代码说明

def generate_expression(self):
        """生成逻辑（仅在计算后校验，避免复杂前置校验）"""
        while True:
        # 1. 随机生成操作数（对应流程图“生成操作数”步骤）
        parts = [self.generate_number() for _ in range(self.operator_count + 1)]
        
        # 2. 随机生成运算符（含冲突避免规则，对应“生成运算符”步骤）
        ops = []
        for _ in range(self.operator_count):
            if ops and ops[-1] in ['-', '÷']:
                ops.append(random.choice(['+', '×']))  # 避免连续减/除
            else:
                ops.append(random.choice(self.operators))

        # 3. 构建表达式（含括号，对应“构建表达式”步骤）
        final_expr = self.add_valid_parentheses(parts, ops)

        # 4. 计算并校验结果（对应“调用evaluate_with_fraction”和“合法性校验”步骤）
        result, is_valid = self.evaluate_with_fraction(final_expr)

        # 5. 保存合法表达式或重试（对应流程图分支）
        if is_valid:
            self.expression = final_expr + " ="
            self.answer = self.format_fraction(result)
            break  # 合法则退出循环，否则继续重试

  def get_unique_key(self):
  """简单去重逻辑（基于结果+操作数）"""
    # 1. 预处理表达式（去除括号和等号，对应“输入表达式”步骤）
    expr_no_paren = self.expression.replace("(", "").replace(")", "").replace(" =", "")

    # 2. 分词（提取操作数和运算符，对应“分词”步骤）
    tokens = re.findall(r'\d+\'\d+/\d+|\d+/\d+|\d+|[+\-×÷]', expr_no_paren)
    if len(tokens) % 2 == 0:
        return expr_no_paren  # 非法格式直接返回原始串
    nums = [tokens[i] for i in range(0, len(tokens), 2)]  # 提取操作数
    ops = [tokens[i] for i in range(1, len(tokens), 2)]   # 提取运算符

    # 3. 计算结果并格式化（对应“计算表达式结果”步骤）
    result, _ = self.evaluate_with_fraction(expr_no_paren)
    result_str = self.format_fraction(result) if result else "invalid"

    # 4. 操作数排序（针对加法/乘法，对应“运算符是否为+或×”判断）
    if len(ops) == 1 and ops[0] in ['+', '×']:
        # 按数值大小排序操作数（解决交换律问题）
        nums_sorted = sorted(nums, key=lambda x: self.parse_to_fraction(x))
        return f"{result_str}_{' '.join(nums_sorted)}_{ops[0]}"
    else:
        # 非加法/乘法保持原始顺序
        return f"{result_str}_{expr_no_paren}"

6.测试运行

import os
import re
import math
import pytest
from io import StringIO
import contextlib
from fractions import Fraction
from main import MathExpression, generate_exercises, grade_exercises, save_to_file


def test_basic_addition_duplication():
    """测试1：加法交换律去重"""
    exercises, _ = generate_exercises(2, 5)
    add_pairs = []
    helper = MathExpression(5)
    for expr in exercises:
        ops = re.findall(r'[+\-×÷]', expr)
        if '+' in ops and len(ops) == 1:
            nums = re.findall(r'\d+\'\d+/\d+|\d+/\d+|\d+', expr.replace('(', '').replace(')', ''))
            if len(nums) == 2:
                num1 = helper.parse_to_fraction(nums[0])
                num2 = helper.parse_to_fraction(nums[1])
                pair = (min(num1, num2), max(num1, num2))
                add_pairs.append(pair)
    assert len(set(add_pairs)) == len(add_pairs), "加法交换律去重失败"


def test_proper_fraction_division():
    """测试2：除法结果为真分数（强化手动校验）"""
    expr_obj = MathExpression(10)
    while '÷' not in expr_obj.expression:
        expr_obj = MathExpression(10)

    # 仅处理1个除法运算符的题目（避免多运算符干扰）
    expr_str = expr_obj.expression.replace('=', '').replace('(', '').replace(')', '').strip()
    tokens = re.findall(r'\d+\'\d+/\d+|\d+/\d+|\d+|[+\-×÷]', expr_str)
    if len(tokens) != 3 or tokens[1] != '÷':
        pytest.skip(f"跳过多运算符题目：{expr_obj.expression}")

    # 手动计算并验证
    a = expr_obj.parse_to_fraction(tokens[0])
    b = expr_obj.parse_to_fraction(tokens[2])
    manual_result = a / b

    # 验证真分数
    assert manual_result.numerator < manual_result.denominator, \
        f"除法结果非真分数：{tokens[0]} ÷ {tokens[2]} = {manual_result}（分子{manual_result.numerator} ≥ 分母{manual_result.denominator}）"
    # 验证程序计算正确
    program_result, is_valid = expr_obj.evaluate_with_fraction(expr_str)
    assert is_valid, f"程序判定除法题目非法：{expr_str}"
    assert program_result == manual_result, \
        f"程序计算错误（程序：{program_result}，手动：{manual_result}）"


def test_mixed_fraction_subtraction():
    """测试3：减法结果非负"""
    expr_obj = MathExpression(10)
    while '-' not in expr_obj.expression:
        expr_obj = MathExpression(10)

    expr_str = expr_obj.expression.replace('=', '').strip()
    result, is_valid = expr_obj.evaluate_with_fraction(expr_str)
    assert is_valid, f"减法题目非法：{expr_str}"
    assert result >= 0, f"减法结果为负：{expr_str} = {result}"


def test_parentheses_validity():
    """测试4：括号不改变运算结果"""
    expr_obj = MathExpression(10)
    while '(' not in expr_obj.expression:
        expr_obj = MathExpression(10)

    expr_with = expr_obj.expression.replace('=', '').strip()
    expr_without = expr_with.replace('(', '').replace(')', '')
    res_with, _ = expr_obj.evaluate_with_fraction(expr_with)
    res_without, _ = expr_obj.evaluate_with_fraction(expr_without)
    assert res_with == res_without, \
        f"括号改变结果：带括号={res_with}，无括号={res_without}"


def test_large_scale_duplication():
    """测试5：大数量生成无重复"""
    exercises, _ = generate_exercises(100, 20)
    unique_keys = set()
    helper = MathExpression(20)
    for expr in exercises:
        helper.expression = expr
        unique_keys.add(helper.get_unique_key())
    assert len(unique_keys) == len(exercises), \
        f"大数量生成存在重复（总{len(exercises)}道，唯一{len(unique_keys)}道）"


def test_answer_format_tolerance():
    """测试6：答案格式容错（UTF-8编码）"""
    fixed_exercise = ["1/2 × 5/3 ="]
    save_to_file('Exercises.txt', fixed_exercise)
    save_to_file('Answers.txt', ["0'5/6"])  # 带分数格式

    success = grade_exercises('Exercises.txt', 'Answers.txt')
    assert success, "批改失败"

    with open('Grade.txt', 'r', encoding='utf-8') as f:
        content = f.read()
        assert "Correct: 1" in content, f"格式容错失败（内容：{content}）"


def test_negative_subtraction_filter():
    """测试7：无负数减法题目"""
    exercises, _ = generate_exercises(50, 5)
    helper = MathExpression(5)
    for expr in exercises:
        if '-' in expr:
            res, _ = helper.evaluate_with_fraction(expr.replace('=', '').strip())
            assert res >= 0, f"负数减法：{expr} = {res}"


def test_division_by_zero_prevention():
    """测试8：无除零题目"""
    exercises, _ = generate_exercises(50, 10)
    helper = MathExpression(10)
    for expr in exercises:
        if '÷' in expr:
            nums = re.findall(r'\d+\'\d+/\d+|\d+/\d+|\d+', expr)
            divisor = helper.parse_to_fraction(nums[-1])
            assert divisor != 0, f"除零题目：{expr}"


def test_multi_operator_duplication():
    """测试9：多运算符题目去重"""
    exercises, _ = generate_exercises(2, 10)
    helper = MathExpression(10)
    keys = [helper.get_unique_key() for helper.expression in exercises]
    assert len(set(keys)) == len(keys), f"多运算符题目重复（keys：{keys}）"


def test_range_limit_warning():
    """测试10：范围不足时程序正常生成"""
    request_num = 1000
    range_limit = 3  # 极小范围，确保组合有限
    try:
        # 核心验证：调用generate_exercises不抛出异常
        actual_exercises, actual_answers = generate_exercises(request_num, range_limit)
        # 辅助验证：生成的题目和答案数量一致
        assert len(actual_exercises) == len(actual_answers), "题目与答案数量不匹配"
        # 辅助验证：至少生成1道题目
        assert len(actual_exercises) >= 1, "未生成任何题目"
        print(f"范围不足测试通过：程序正常生成{len(actual_exercises)}道题目")
    except Exception as e:
        # 若抛出异常则测试失败
        pytest.fail(f"范围不足时程序崩溃：{str(e)}")

测试覆盖率

7.实际花费时间
见前表

8.项目小结
本次项目不仅完成了小学四则运算程序的开发，更让我们掌握了 “需求分析→设计→编码→测试” 的完整流程，以及结对开发中的沟通与协作技巧。未来将把 “先设计后编码”“分阶段测试” 的经验应用到更多项目中，同时针对本次暴露的问题，持续优化算法，提升程序的实用性。
我们采用了本地线下的结对，桌子够大，屏幕够大，给了我们良好的结对环境。
成员1对成员2评价：逻辑思维缜密，在设计函数时，能精准预判减法非负、除法真分数等校验规则，并用栈式计算优雅处理运算符优先级，核心算法的健壮性很强。
成员2对成员1评价：测试意识强，能从用户角度提出 “答案格式容错”“范围不足时的友好提示” 等细节需求，编写的测试用例覆盖了 80% 的核心分支，有效降低了 bug 率。