NSSCTF刷题日记day4：[CISCN 2023 初赛]badkey

题目如上，是CISCN上面的一个密码题目，然后环境是使用nc连接的，但是给了源码。

先是根据附件的源码，写出第一个破解的脚本，这个并不困难。

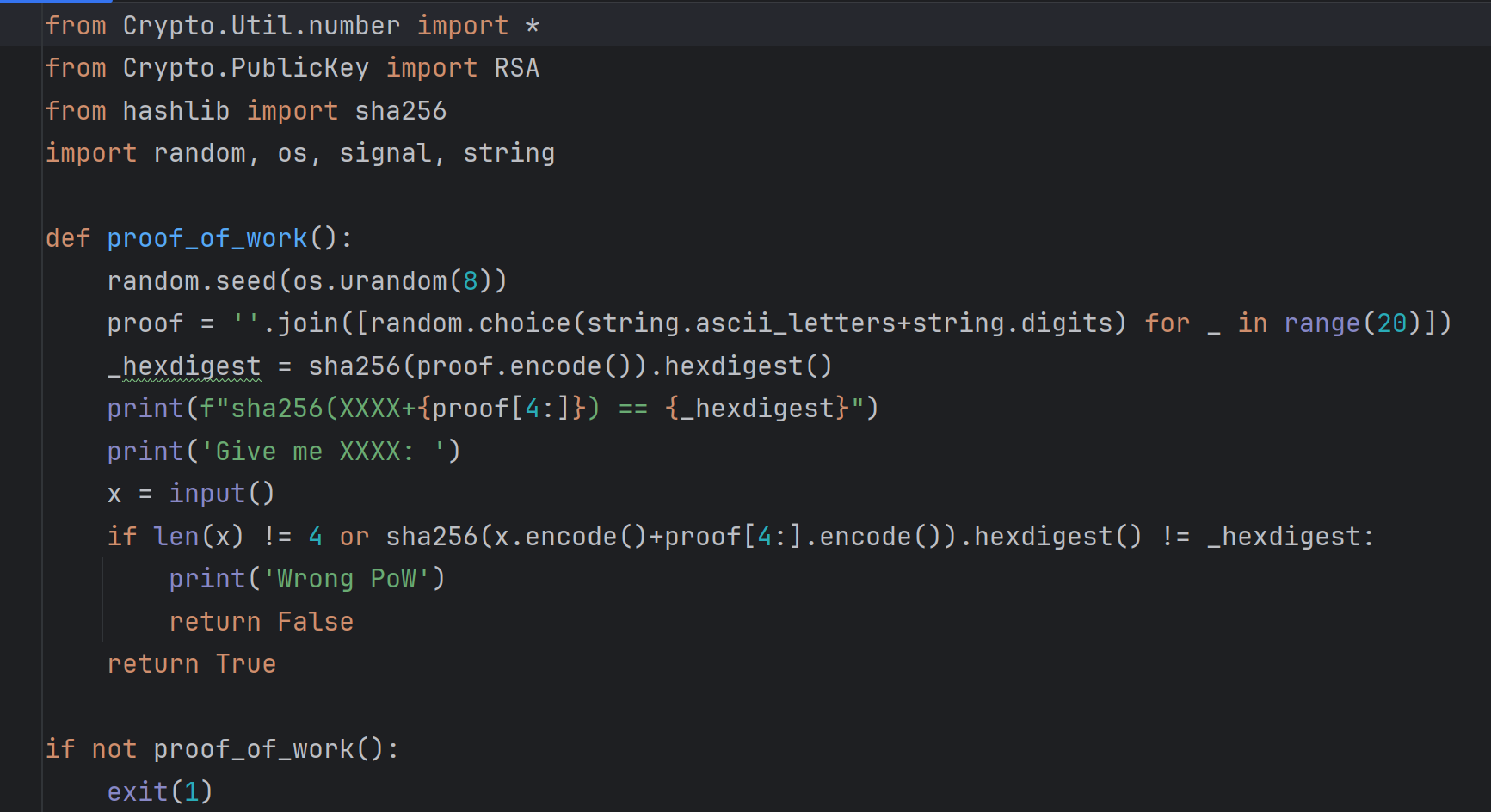
hash爆破的脚本如下:

import hashlib
import string
from itertools import product#使用product生成笛卡尔积来生成组合字符串。
sha256table=string.ascii_letters+string.digits
knowstr='scZclxeouXzNinz0'
for ab in product(sha256table,repeat=4):#指定字符长度为4
    tmp=''.join(ab)+knowstr
    des='97c15e18565aa3a2bbe1edf7065b5f8092b34b0836526ecd236d879ac4cfedc9'
    if hashlib.sha256(tmp.encode()).hexdigest() == des:
        print(''.join(ab))

由于每次连接的时候其的hash值和已知字符串部分是会改变的，所以每次都需要更新，现在我们去看看第二个部分的解密源码部分。

可以从源码中看到。

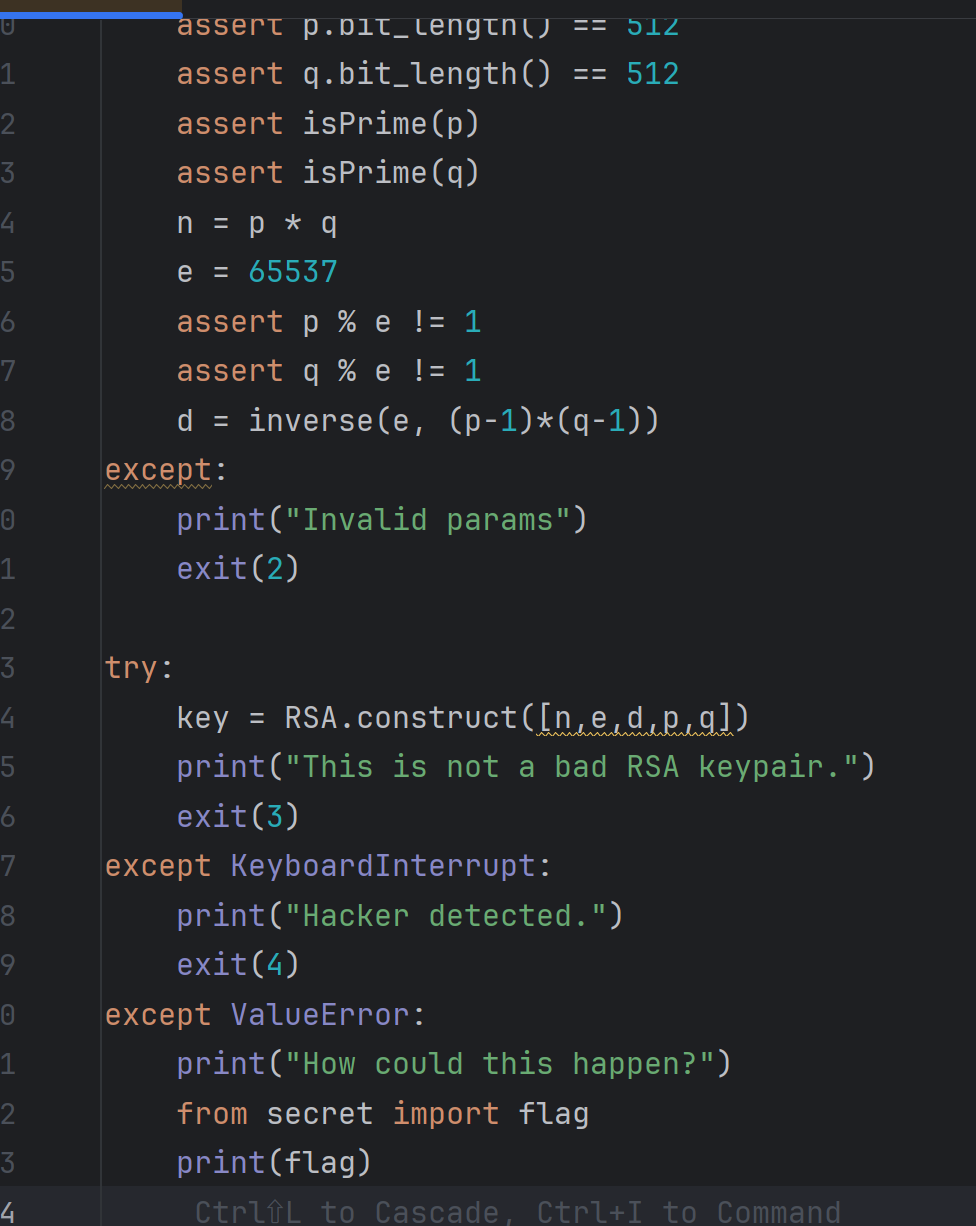
当输入的p和q导致其相关函数抛出了ValueError的异常情况的时候，就会让flag被输出出来。然后我们去问问ai看看有什么情况会导致整个函数出现那样的异常情况。

从ai给出的情况进行筛选可以使用的方法。首先我们只能输入p和q，所以关于改变e，d，n的情况都舍去，并且因为参数的数量传入也是固定的，所以这个也舍去，然后最后可以看到可以尝试的方法有三种：

首先是第一种，就是p和q相等，不过我们得自己生成一个。

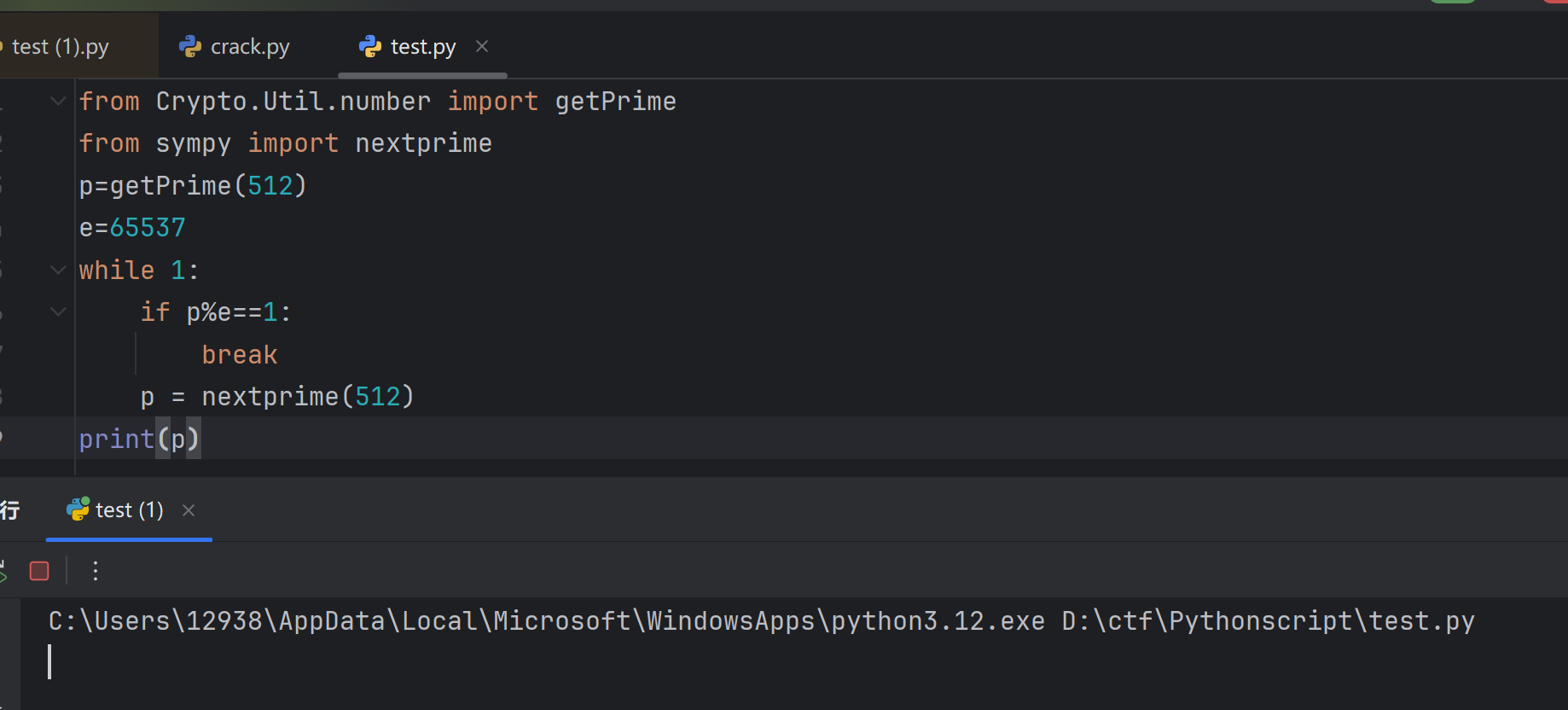
这个时间开销太大了，如果使用生成512位得全部个数然后去验证，也是很大得开销。所以我们得尝试一下通过pq导致d与n不互质，p和qmode===1得情况也被排除了。也就是说，gcd(d,n)!=1。

简单思路得代码脚本是说生成两个512位的素数，然后组成n，然后求d验证d跟n是否互质，如果互质就输出这对p和q，但是时间开销很大，我们假设有n和候选的512位的素数，这种方法的时间开销是O(n^2)，所以实际上开销是很大的。

所以我们得尝试减小时间开销，若要让d和n不互质，其最本质就是让其最大公约数不是1就可以。所以假设我们得到一个素数p，那么要让条件成立就应该存在约束条件d=mp,n=pq,然后由于有e*d === 1(mod(p-1) * (q-1))，由于q是未知的，所以关于n的式子是无法化简得，但是在关于e的式子中只有q是未知的，d可以由m * p求得，所以由e * m * p === 1(mod(p-1) * (q-1))，将其变为e * m * (p-1)，发现与原式相差一个e * m所以加上，最后又取模p-1，最后又e * m === 1(mod(p-1)),然后就可以得到在前置约束条件下e跟m的关系，并且可以直接通过e求得满足前置条件的m，这下m也由p可以直接得到，剩下q，然后把e * m * p === 1(mod(p-1) * (q-1))重新整理一下发现可以变成：q=(e * m * p -1)/((p-1) * k ) + 1，然后k的范围其实也很好推导得到：k是属于(1,e+1),首先是m为e的逆元在p-1下，所以其肯定小于(p-1)，继续推导就可以得到k的范围了，最终得到了如下的脚本：

e = 65537
while True:
    p = getPrime(512)
    k1 = inverse(e, p - 1)
    t = (e * k1 * p - 1) // (p - 1)
    for k2 in range(1, e + 1):
        if t % k2 == 0:
            q = t // k2 + 1
            if isPrime(q) and q.bit_length() == 512:
                print(p, q)
                exit()

脚本是我找别人的捏，不过逻辑能理解就好，因为如果这个p合适的话，那么通过其求出的q也会是整数，所以在第一个if条件才会判断其是否能被k2整除，k2是我们推到式子过程的k，而k1是(e * m * p -1)/(p-1)的整体，当能整除的时候看其是否满足判断条件，满足则输出，同时还要确保q是512位。

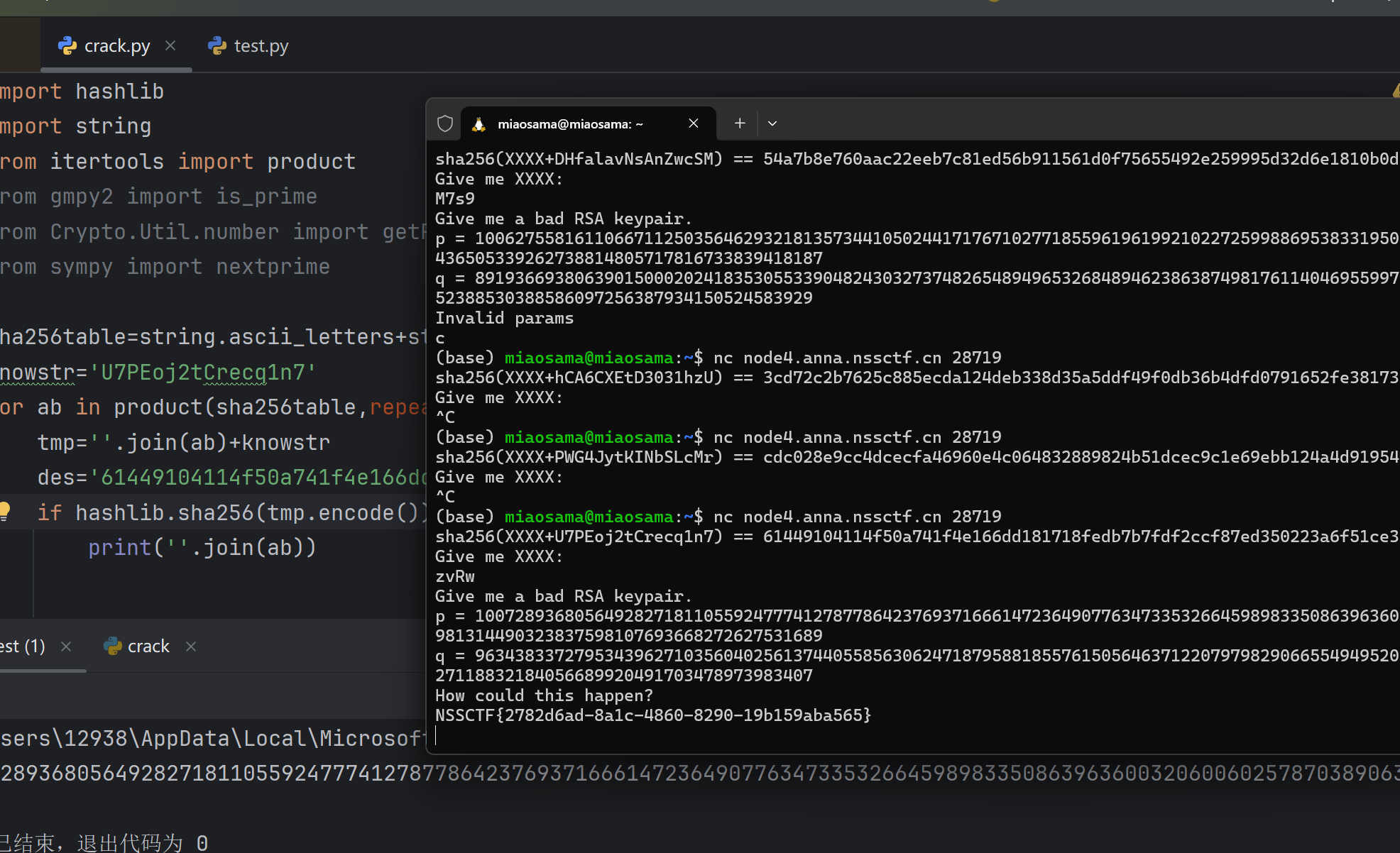
最后夺旗成功。get daze。