ctfwiki:RSA的详细分析与总结

本文通过学习ctfwiki上的RSA解密的方法从而写出自己的理解，总结，或是一些细节的小补充。（博主语文不好，可能出现用词不当）

目录

模相关攻击
公钥指数相关攻击
私钥d相关攻击
Coppersmith 相关攻击
RSA选择明密文攻击

RAS的原理

关于RSA的加密和解密的原理的说明和推导的视频网上一搜一大堆，这里不进行赘述，随笔两句关键的地方就是，公钥(e,n)私钥(d,n)，还有phi=(p-1)(q-1)。还有一个重要的由于e跟d互质有的一个关系e*d $\equiv$ 1(mod phi)。加密用公钥，解密用私钥。

而在做题过程中的rsa大多数情况都是让我们想办法求得私钥，或者利用密文的数学关系绕过私钥去解密。

基本工具

wiki里面给的工具都各有各的用途，而我感觉最有必要的工具就是openssl。

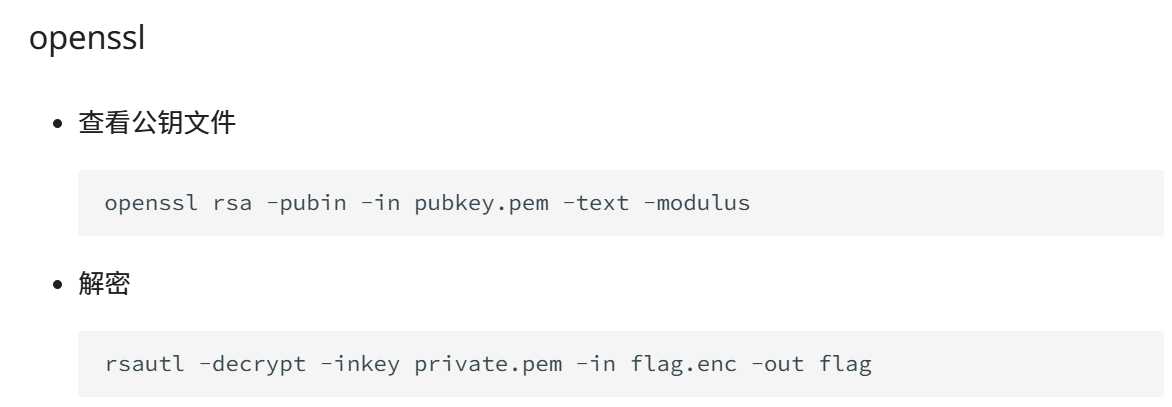
在rsa中的最有用的命令就是wiki上面给出的这两条命令。

查看pubkey.pem文件中的信息，第二条就是解密了。
openssl rsa -pubin -in pubkey.pem -text -modulus
rsautl -decrypt -inkey private.pem -in flag.enc -out flag

然后其它的了解即可，wiki里面的这些内容放在最前面的位置，但是博主以前并不是很乐意读所以因为这种文件吃亏过。所以这里最先讲pen和enc文件是从何而来又如何解密。

这里还给出一种没有openssl的解密思路。如果用不了openssl，就使用在线网站解析pubkey里面的信息，然后想办法解出d，最后以二进制的形式读取flag.enc文件，因为enc文件本身就是二进制的格式，读取之后使用推导得出的d进行正常情况下的rsa解密就可以。

wiki给出的在线分解工具：https://factordb.com/

还有本地的yafu分解n，yafu本地部署github上搜素即可

python3可能会用的库：

gmpy2库:pip install gmpy2

pycrypto库:pip install pycryptodome

模相关攻击

暴力分解n

wiki给出的条件是当n小于512比特位的时候。
这里我给出一个代码可以快速看出n的比特位数。

int(bin(n),2).bit_length()

在cmd中输入python然后输入以上指令。只要小于512就可以尝试yafu或者是factordb的网站进行分解。

p和q选取不当分解n

前面的情况是n的数值没控制好导致其容易被分解，这里是说p和q没选取好，包含n大于512比特位数的情况也是有可能的。

p和q相差很大

结论就是不怎么行，所以跳过。

p和q相近（p-q的绝对值很小）

import gmpy2
from Crypto.Util.number import inverse

p=123456789
n=123456791
def shifoukekaifang(num):
    if num < 0:
        return False
    root,f=gmpy2.iroot(num,2)
    return f

n_sqrt,_=gmpy2.iroot(n,2)
if nsqrt**2<n:
    n_sqrt+=1

f=0
for a in range(0,5000):
    x=n_sqrt+a
    #print(shifoukekaifang(x**2-n))
    if shifoukekaifang(x**2-n):
        y=int(x-n_sqrt)
        p,q=x+y,x-y
        #print(p,q)
        phi=(p-1)*(q-1)
if f==0:
    print("none")

如果在大于300都还没找到的话，那大概不是p-q相似了。（大概是相我似了）
补充：最近打比赛写到御网杯的一个crypto正好写到一个p-q很小的题目，然后写的时候发现一个关键的点就是，一定要确保n_sqrt的值是根号n向上取整数的。

p-1光滑

我写过一篇文章讲p-1光滑。
https://www.cnblogs.com/miaosamakawayii/p/18847394

p+1光滑

这个真想搞懂的还是建议啃wiki上面的，已经写的很详细也没有上面需要补充的细节，并且因为其数学关系相当复杂，用于加密和出题都比较难变化，如果出了大部分直接从wiki上面搬的脚本改一下数值和细节就可以解题。

模不互素（不互质）

原理和判断条件写的很简洁，而且代码也是很好写的，但是为什么这个原理可行wiki上没给出很明确的说明和推理。也许对一些数学好的人是一眼就能理解，不过我觉得能让知识被更多人更大深度地被各种各样的人所理解才更好。这里给出一点补充的数学小推论：
当n1和n2不互质的时候，那么证明p1*q1与p2*q2不互质，也就是说gcd(p1*q1,p2*q2)!=1。现在给出如下的推导过程：
设n1=p1*q1,n2=p2*q2,且有gcd(n1,n2)!=1
因为n1和n2不互质，所以p1*q1与p2*q2有非1的最大公约数。
假设p1$\ne$p2,q2，且q1同理。
因为其存在非1最大公约数，假设为a*p1=p2
所以有n2=p2*q2=p1*a*q2
所以n1与n2求最大公约数时，则其值为p1。
同理可得，其它得情况仍成立。

以上就是我对模不互素得数学推导过程。

共模攻击

Wiki上给得很明确了，只需要了解扩展欧几里得得原理就就好：
扩展欧几里得说得是，假设有两个数x，y互质，那么一定存在一个整数a和整数b使得ax+by=1mod(n)。且a,b分别是x,y的在模数n下的乘法逆元。

RSA，p ^ q=leak

这个题目是打HXCTF的时候遇到的题目，然后上网一搜相关信息发现还有这种的p和q的出题方式，于是补充到模相关攻击里面来。
学习资料来源于：https://skatexu.github.io/2023/11/30/RSA-p-q/

文章里面提到这个东西最关键的就是一个剪枝爆破的方法，用对比的说明会比较容易理解，在之前的大多数爆破方法都是一种针对整体的具体数值进行爆破的方法，然后wiki里面提到的有类似剪枝相关的操作的就是coppersmith的方法（下文有提到），剪枝爆破的方法主要操作对象为将其转化为二进制数据然后进行一个逐位爆破，而异或的操作在处理二进制数据的时候因为其本身的性质导致其会造成一种在二进制上数据信息泄露的作用，所以对于leak的爆破方法才会需要使用一种剪枝爆破去恢复一个大素数。

其中最简单的就是:leak=p ^ q,因为生成p和q的时候通常使用getPrime()函数，所以在p和q的最高那一位数上必定是1，所以p ^ q则导致leak的最高位必定是0，所以也就导致了leak必定没有跟p和q同样的位数，所以在进行剪枝爆破的时候，需要先利用函数zfill将leak合理地跟p和q的位数对齐，

处理p ^ q的剪枝爆破的关键函数为：(以下函数来源于上面提到的文章的函数，我将其讲的更易懂点)

def pq_high_xor(p="", q=""):  #若有已知的p或q的一部分高位数，其的二进制会以字符串形式传入
    lp, lq = len(p), len(q)   #获取其二进制字符串的长度
    tp0 = int(p + (512-lp) * "0", 2) #
    tq0 = int(q + (512-lq) * "0", 2) #左边的四个为p和q的高位后补0或补1。
    tp1 = int(p + (512-lp) * "1", 2) #当全补充0，tp0 * tp0 <n,当全补充1，tp1 * tp1 > n
    tq1 = int(q + (512-lq) * "1", 2) #所以左边是做一个约束条件，约束最后求得的值的范围

    if tp0 * tq0 > n or tp1 * tq1 < n: #爆破到不满足约束条件的直接舍弃
        return
    if lp == leak_bits: #满足约束条件并且已经恢复到跟原来p和q相同位数则添加值再返回
        pq.append(tp0)
        return

    if xor[lp] == "1":                #两种异或值情况,xor=1，则当前位数p和q不相同
        pq_high_xor(p + "0", q + "1") #
        pq_high_xor(p + "1", q + "0") #p当前位数为1,q为0m,或者相反
    else:
        pq_high_xor(p + "0", q + "0") #xor=0的情况
        pq_high_xor(p + "1", q + "1")


def pq_low_xor(p="", q=""):
    lp, lq = len(p), len(q)
    tp = int(p, 2) if p else 0
    tq = int(q, 2) if q else 0

    if tp * tq % 2**lp != n % 2**lp:
        return
    if lp == leak_bits:
        pq.append(tp)
        return

    if xor[-lp-1] == "1":
        pq_low_xor("0" + p, "1" + q)
        pq_low_xor("1" + p, "0" + q)
    else:
        pq_low_xor("0" + p, "0" + q)
        pq_low_xor("1" + p, "1" + q)

两种爆破方法的约束条件都如下:

建议从高位到低位爆破，这样需要添加的约束条件会少一点。

然后这种攻击还有另外的一些变种,如leak=p ^ (q >> 100)这样子的，这个由于右移导致p的高位数直接反映在leak里面所以可以直接爆破出p,然后得到与之对应的q。

再有的变种会导致p和q的位数丢失，所以需要用coppersmith攻击恢复丢失的位数，从得到其完整的值。比如:leak=(p ^ q) >> 100这样子的。
先使用剪枝爆破出p和q的高位数，然后使用coppersmith攻击恢复出完整的一个p或者q即可，然后通过n/p看是否为整数验证求得的p，得到q的值

coppersmith的相关脚本参考wiki上面的，主要使用sage脚本进行求解。

公钥指数相关攻击

小指数e攻击

由于e=3的指数实在是太小，所以基于这种的攻击方法大多数思路是一种是对于处理c到m的过程，直接对c进行一种开立方直到开出整数的的结果，但在实际做题的过程实际上我们还可以添加一个验证前缀和的操作来增强其解密过程的正确性：

可以看到m和c的关系是很容易计算得出的，然后直接进行一个枚举，因为e=3所以m跟c其实是呈现线性的关系，所以一般情况是一定可以求出来的。
然后对于e=2，其有本身独特的算法，不过对于以上的方法，其实也是可以的，但wiki上面提出的方法更有效率。

rabin算法（e=2）

对于其给出的算数式子是不难记住并且也不难编写成代码的。
但是对于真正地理解还是需要花点心思的。

首先直接看解密，解密部分的前面部分不难理解，解密后面的部分也不算复杂，而从前面到后面的话就有点跳跃性了，其实如果细心点学习的话，不少人跟我应该差不多，看到这里就是一句“啊？”的，就是abcd这一部分是特别跳跃的，然而在了解原理之后也让我对wiki的作者们更加崇拜了（叠buff，别喷我）

现在直接到“解密出四个明文”的地方，为什么abcd解密出来之后就是原来一段明文的四个段了。在反复观摩数学式子和下面的代码，最先发现的是这个yp和yq分别是p，q在模数q，p下的乘法逆元，然后因为c是在m^2modn 下的一个解，，由于函数式子为平方，所以其具备偶函数的性质，是对称的，所以对于c的话，m就会有2个值跟它对应，当然对于明文我们都知道应该是一个正数，但这里先当作数学问题处理。然后当我们把n变为p*q然后把c进行开方，然后分别模p和q,mq=m(modp)=(c^2/1(modpq))modp=(c^2/1)modq,实际上mq是如此推出来的，mp同理，现在我们可以知道mp，不仅是关于c的一个解，同时其也是关于m的一个解。

当mp为关于c的解的时候，因为其是在modp下进行计算的，所以可能解有mp和p-mp，而mq同理，所以可以知道在p和q的模数下m关于c的各有两个，然后对这四个解进行一个拼接，拼接方法为CRT（中国剩余定理），因为我们最终求得并非单独得p或q下的解，而是n的解，所以以(mp,mq)为最优先，并且mp与之可能等价的解有p-mp，mq有q-mq，从而通过CRT算出在n下的解。
（突然发现写的有点多了。。）

结论：
如果n可以进行分解，对于e=2还有这种情况进行求解（不过n
都分解了也许直接用标准的rsa解密会更快？）

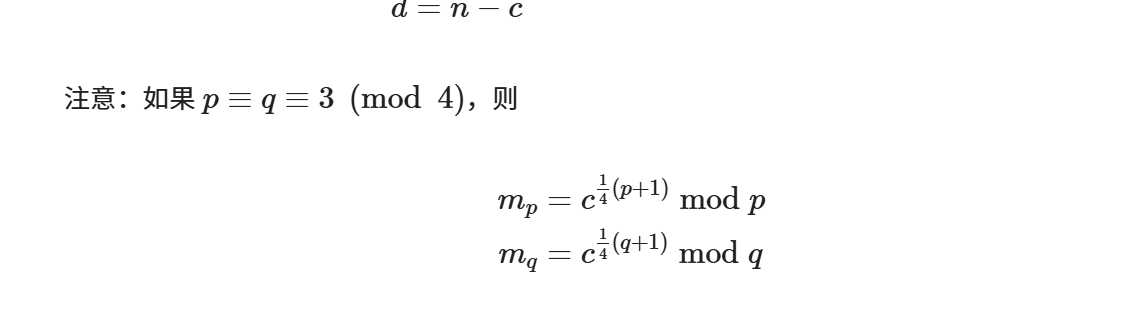
求得之后在代码中求abcd得操作，用sympy库里面得crt函数，以(mp,mq),(mp,q-mq)(p-mp,mq)(p-mp,q-mq)得四个组合进行求解，求的也是一样的。

低指数e加密广播攻击

这个特征还是e很小（e=3），然后对明文进行多组n加密成多组c，本质上其实就是解一个同余方程组，使用CRT就可以进行求解，sympy库里面有这个库里面有crt函数，可以直接用crt进行一个同余方程组的秋季问题，最终解就是明文，因为e很小，所以直接开立方也是正确的（换成数学的说法就是因为立方是呈现一种线性关系，所以直接求得偏差很小很小）。
因为使用同一个e进行加密得化就是m^e同时是n1,n2...,和c1,c2...对应方程组的解，也就是说m^e满足所有同余方程组，所以直接最终问题就转化为了一个求解同余方程组的问题。
下面还会继续讲解更深刻的原理。

公因素攻击

题目给出的多个nc之后，当nc多了之后，可能出现两个n之间不互素的问题，所以当对这两个n求共因数的时候必定为其共有的p和q，因为出现的n=p*q，所以对不互素的n求gcd一定会得到求得的一个共有的p，然后选取这一组，来进行n的分解从而进行攻击。

私钥d相关攻击

wiki貌似就给了一个d泄露攻击（还是说是因为我部署的本地的wiki的问题）

这里就总结一下我自己做题和看别人的文章看到的d相关的攻击。

dp泄露攻击

dp泄露攻击的脚本和明文原理一艘一搜一大堆，所以我主要写一下关于其数学关系推导的过程把。
首先得知道dp的定义，dp=dmod(p-1)，然后我们又知道关于e和d之间有ed恒等于1(modphi)的关系，然后我们把第一个式子两边同时乘上e就有,dp * e = e * d mod(p-1)，然后对于这个式子我们有dp * e+k1 * (p-1) = e * d，而对于恒等式，我们有e * d=1+k2 * (p-1) * (q-1)，然后就有等式:dp * e+k1 * (p-1)= 1+k2 * (p-1) * (q-1)，最终化为:dp * e -1=(p-1) * (k2 * (q-1)- k1)然后我们设i为(k2 * (q-1)- k1),变为:dp * e -1=i * (p-1),因为dp小于(p-1)所以e大于i,从而确定i的范围从(1,e)，因为i要作为除数，所以i除去0，最终回代到n=p*q中进行验证。

dp,dq泄露攻击

这个有篇文章讲的已经很详细的。
https://blog.csdn.net/m0_51507437/article/details/122440936
这篇文章对dp和dq的泄露攻击，进行了较为详细的推理。
总结就是通过dp和dp绕过求d而直接求c^d的值，然后直接解密出明文。

Coppersmith 相关攻击

coppersmith的基本原理不进行讲解（因为我也没看懂），但是不影响讲解下面的一些攻击方法。

Basic Broadcast Attack（基本广播攻击）

这个东西在e攻击里面简单讲了一下。

这里补充一下它的讲法，这个C就是c1c2c3进入crt里面解同余方程组，因为m³=mmm，然后m分别小于n1n2n3,所以利用放缩就变成m³ < n1n2n3,因为m³=Cmod(n1n2n3)，就等式而言，C=m³或者N-m³，但是在前提假设条件下，m³ < n1n2n3，从而可以直接舍弃掉mod(N)，最后证明C是等于m³的，这种密文的特征跟公因数攻击有点相似，当n不互质就可以直接进行公因数攻击分解n，所以判断是广播还是公因数，一个是看e，一个就是求各个n之间的gcd的值，是否为1。
并且这里还扩展到了e比较大的情况，就理论的情况而言，假设当e为65573的时候，可能其理论上需要的密文对就是65573对，但是实际上可能更少，不过其解密过程还是一样的，就选取了多少对，对之后求出来的密文进行多少次开方，就理论上是这样的，但实际上并不是很可行。只是针对在密文对数上尽可能少的情况下可行，对于那种超过10组以上的，可以优先考虑公因数。

Related Message Attack（相关消息攻击）

第一次见这个解密是在TGCTF上（https://www.cnblogs.com/miaosamakawayii/p/18831273#2.）
然后wiki上面给了完整的数学推导，所以这里不进行赘述，然后关于原理最需要花点时间理解的就是：

这一部分。

首先是x-M2代表什么，这里给出了解释说明x-M2是一个关于M2的一次多项式，给出的例子中假设g(x)是以M2为根的多项式，那么g(x)就可以写成a * (x-M2) * h(x)，当x=M2带入进去多项式的时候，g(M2)=0，所以这也就是当M2为根的时候，可以得到x-M2是多项式除法中的可以整除其的因子，然后结合攻击原理中，因为M1跟M2呈线性关系，所以得到了M2也就得到了M1，所以这里以M2为主。
因为M2是第一个f(x)^e-C1的解，且是x^e-C2的解，所以可以知道x-M2是两个式子的一个公因数，所以用gcd求两个式子的公因数的时候是可以求得a * (x-M2)，然后在sage脚本中用monic操作让其除以最高次的系数就可以变成x-M2,然后在sage语法中脚本中用[b]可以直接提取b次项的系数，从而得到了-M2，最后返还其得负值就是M2,从而得到了M1。
wiki脚本(修改了一点)：

import binascii
from Crypto.Util.number import long_to_bytes
from sage.all import *

def attack(c1, c2, a,b, e, n):
    PR.<x>=PolynomialRing(Zmod(n))
    g1 = x^e - c1
    g2 = (a*x+b)^e - c2

    def gcd(g1, g2):
        while g2:
            g1, g2 = g2, g1 % g2
        return g1.monic()#转化为首一多项式（即最高次项系数为1）
    return -gcd(g1, g2)[0]

c1 = 0x547995f4e2f4c007e6bb2a6913a3d685974a72b05bec02e8c03ba64278c9347d8aaaff672ad8460a8cf5bffa5d787c5bb724d1cee07e221e028d9b8bc24360208840fbdfd4794733adcac45c38ad0225fde19a6a4c38e4207368f5902c871efdf1bdf4760b1a98ec1417893c8fce8389b6434c0fee73b13c284e8c9fb5c77e420a2b5b1a1c10b2a7a3545e95c1d47835c2718L
c2 = 0x547995f4e2f4c007e6bb2a6913a3d685974a72b05bec02e8c03ba64278c9347d8aaaff672ad8460a8cf5bffa5d787c72722fe4fe5a901e2531b3dbcb87e5aa19bbceecbf9f32eacefe81777d9bdca781b1ec8f8b68799b4aa4c6ad120506222c7f0c3e11b37dd0ce08381fabf9c14bc74929bf524645989ae2df77c8608d0512c1cc4150765ab8350843b57a2464f848d8e08L
n = 25357901189172733149625332391537064578265003249917817682864120663898336510922113258397441378239342349767317285221295832462413300376704507936359046120943334215078540903962128719706077067557948218308700143138420408053500628616299338204718213283481833513373696170774425619886049408103217179262264003765695390547355624867951379789924247597370496546249898924648274419164899831191925127182066301237673243423539604219274397539786859420866329885285232179983055763704201023213087119895321260046617760702320473069743688778438854899409292527695993045482549594428191729963645157765855337481923730481041849389812984896044723939553
e=3
a = 1
id1 = 1002
id2 = 2614
b = id2 - id1
m1 = attack(c1,c2,a,b,e,n)
print(long_to_bytes(m1-id1))（根据加密代码进行还原）

Coppersmith’s short-pad attack(短填充攻击)

这里还是先上wiki的截图

这里我们可以知道为什么会出现这个攻击，出现的首先原因就是为了让rsa的加密安全性更高，所以对明文随机的填充。然后当这个padding过小的时候，就会导致其容易被攻击。
然后wiki对这种攻击进行了原理上的解释，这里假设模数N长度为K（这里实际上指的是比特位），而m是指填充得比特位数，并且对于k/e^2其的数值一般都是要求向下取整数。
然后这两个表达式是这样得到的:
M1=2^m·M+r1
M2=2^m·M+r2 ,因为M1-r1=2^m·M。
所以可以推导得到关系式子:M2=M1+r2-r1
然后又有C1=M1^e mod N
C2=M2^e mod N ,C2=(M1+r2-r1)^e mod N
然后把C1和C2右移，设M1为x，r2-r1为y,则有:
0=x^e - C1 mod N ,0=(x+y)^e -C2 mod N
所以就可以转化为解方程组:
g(x,y)=x^e - C1 mod N (1)
g(x,y)=(x+y)^e - C2 mod N (2)
所以可以知道M1就这两个方程组联立之后求解得到的x的值。
可以用z3求解器或者sagemath来求解。（推荐sagemath）

import z3
C1=_
C2=_
e=65573
x=z3.Int(name='x')
y=z3.Int(name='y')
s=z3.Solver()
s.add((x*y)**e-C2)
s.add(x**e-C1)

if s.check() == z3.sat:
    print(s.model())
else:
    print("无解")

也不知道wiki作者是忘了还是没有写，这里我给出一个z3的脚本(并非完全是这样的，可以根据情况添加约束条件条件)，sage也差不多。

Known High Bits Message Attack

这个没什么好说的，就是一个满足coppersmith约束求解的问题。具体参考wiki给的github上的连接：https://github.com/mimoo/RSA-and-LLL-attacks
已经讲的很详细了。

RSA选择明密文攻击

这个部分wiki上面讲的很清楚，不说了捏，如果之后再看到其相关的特殊的例子再进行补充