TGCTF re crypto wp
TGCTF re
目录
crypto
1.AAAAAAAA·真·签到(复现)
2.tRwSiAns
3.宝宝rsa
4.费克特尔
5.mm不躲猫猫
Reverse
1.Base64
2.xtea
3.蛇年得本命语言(复现)
4.水果忍者(复现)
5.exchange
crypto
>
1.AAAAAAAA·真·签到(复现)
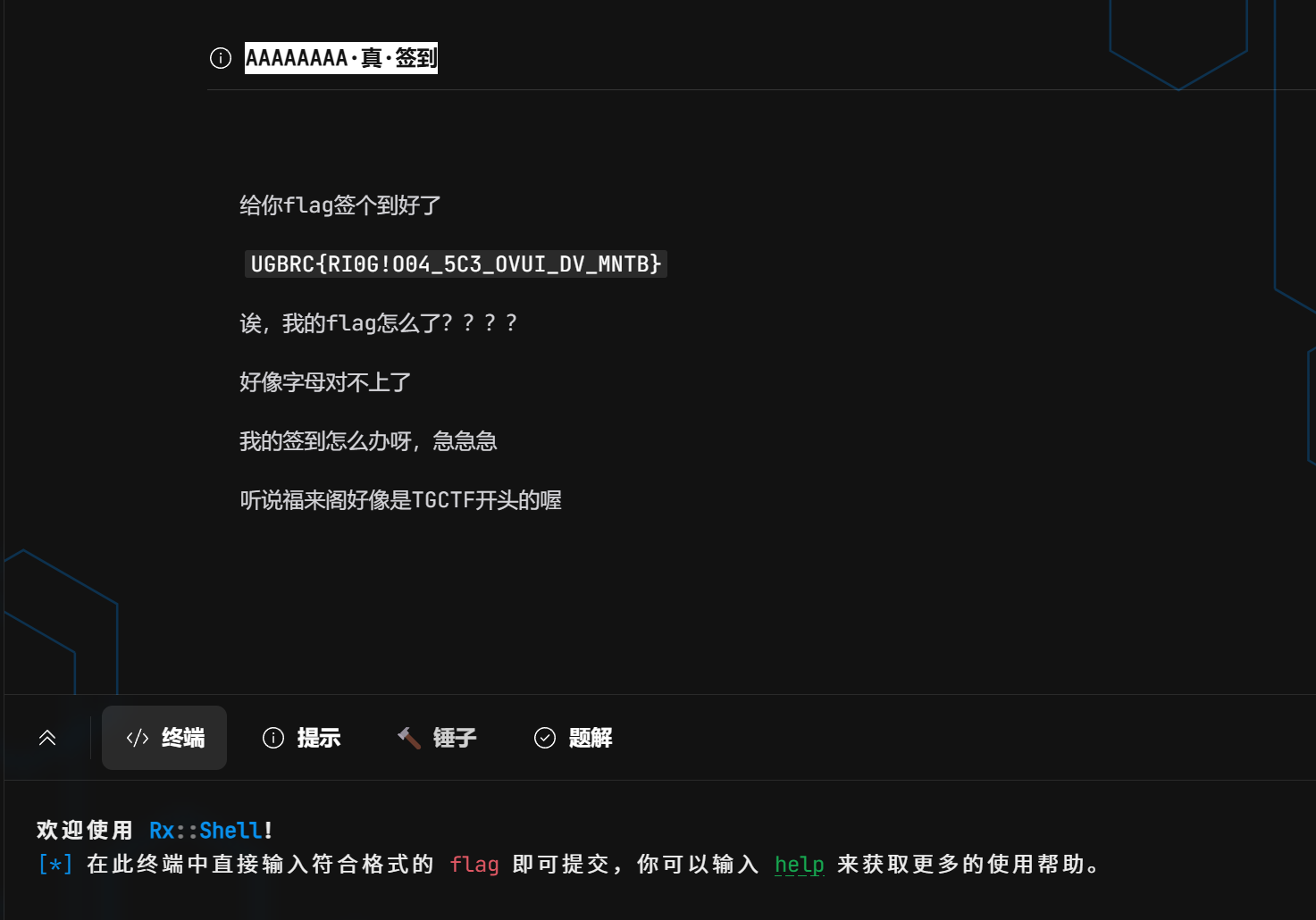
实话实说,这道题目其实挺简单的,就是把每个字母的字符分别等差位移,遇到每一个字符偏移都会多1,但是特殊字符和数字不偏移,仅仅让j加1,然后再偏移的时候需要将其对应的索引始终保持再A~Z之间,比赛的时候也是因为忘记规范从而没有算出正确结果。
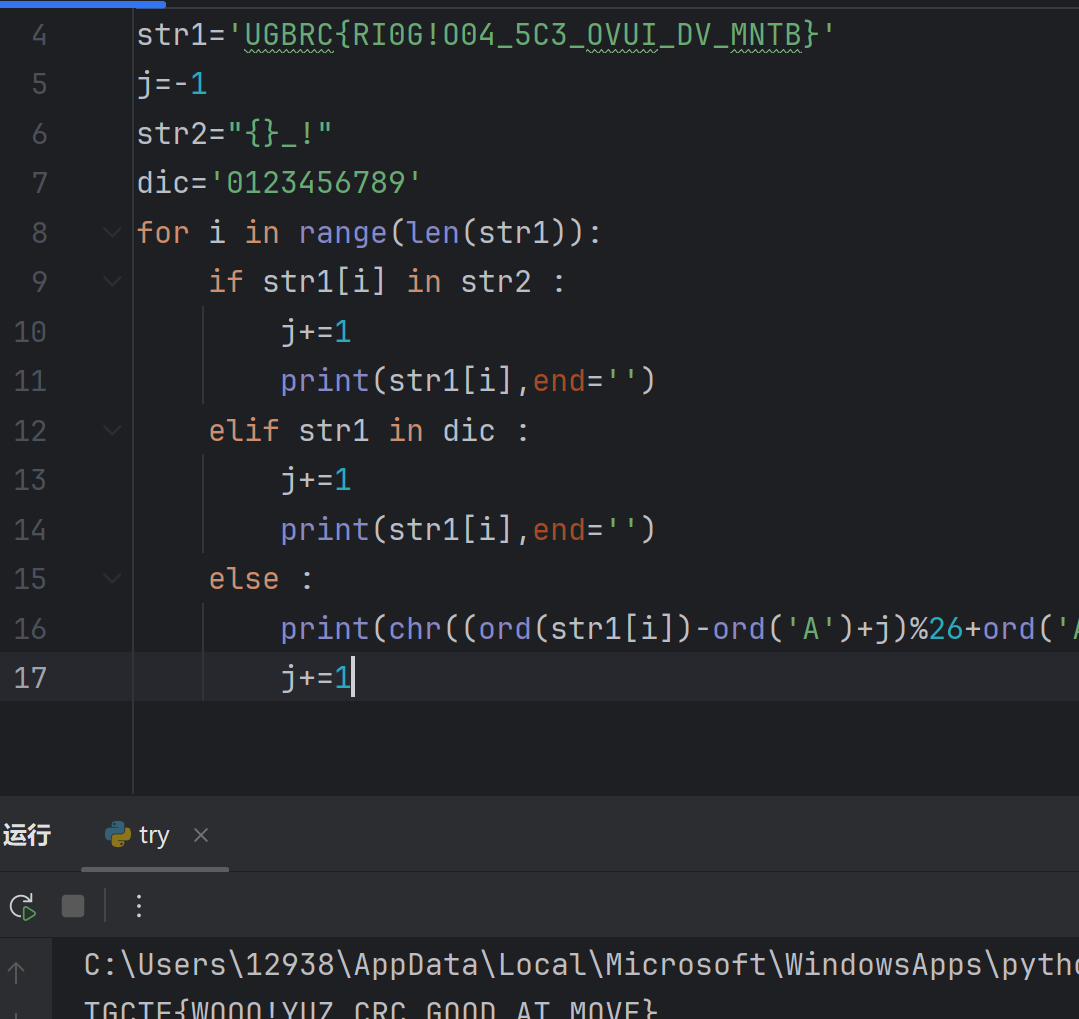
这里复现的时候我在输出字母的时候加上了规范,最后得到了正确的flag了。
总结:这里踩坑的地方是在做变种凯撒的时候忘记对其字符串进行规范操作从而导致无法得出正确的flag。
TGCTF{WOQO!YUZ_CRC_GOOD_AT_MOVE}
>
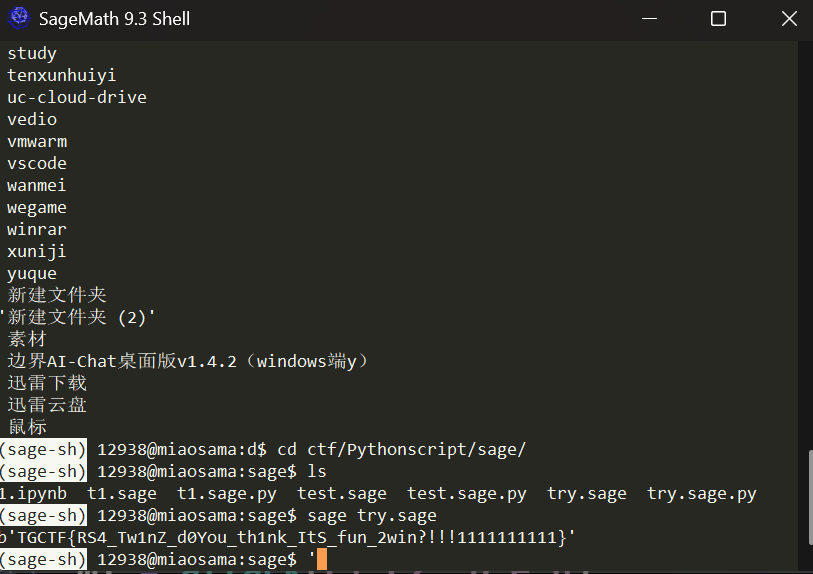
2.tRwSiAns
下载题目之后打开文件看到如下信息。
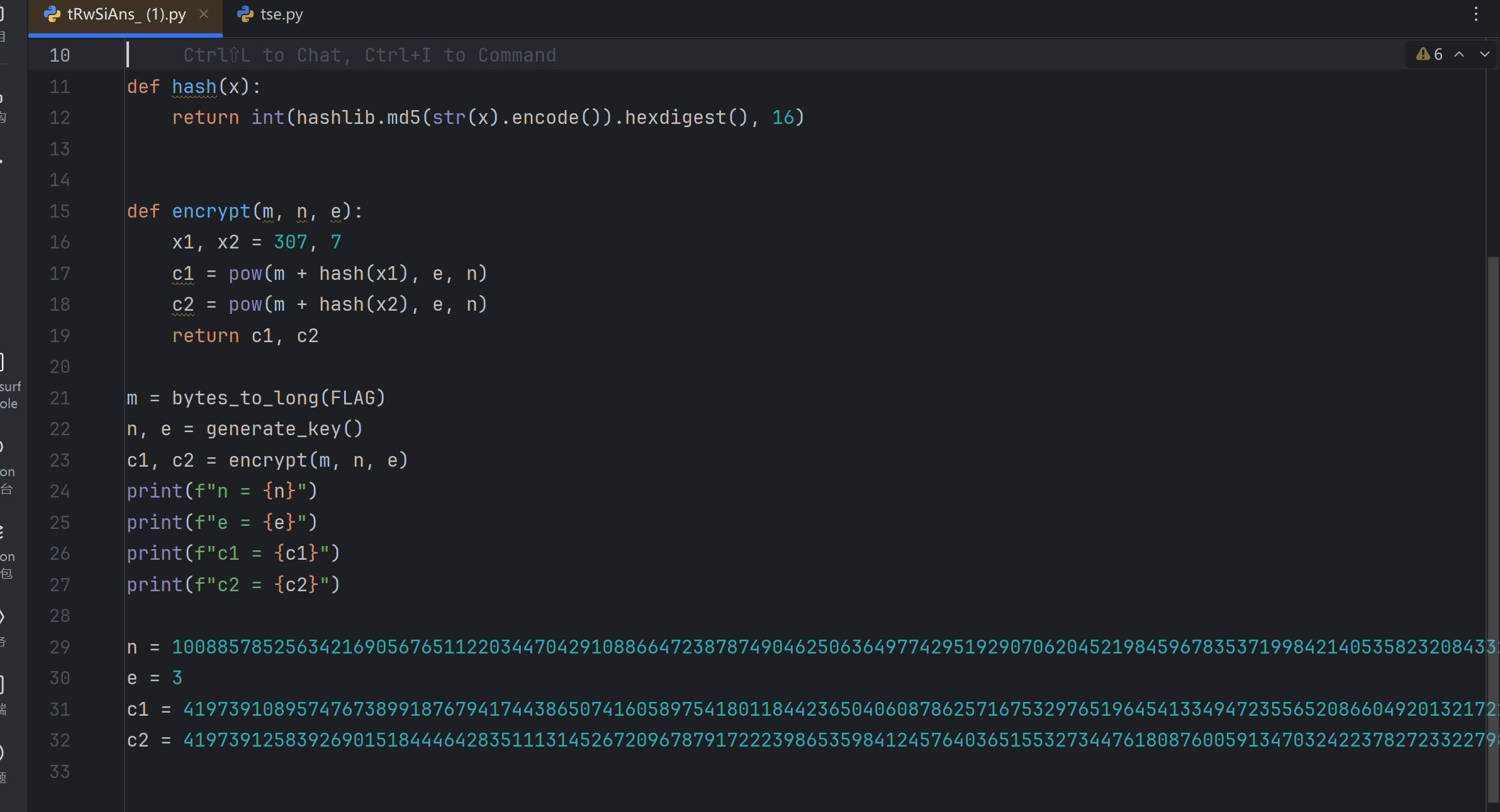
得到的信息是n,e,c1,c2第一此我还以为是共模攻击,然后去使用共模攻击的脚本进行尝试最终发现,其的e值很小,主要应对的是对e值很小的情况下的攻击,最后在ctfwiki里面看到相关消息攻击,就是当消息m被同一个模数的情况下被加密成两段密文,并且密文之间存在一定的线性关系,并且wiki中给出解释说当e为3的时候,其的密文一定有线性关系,那么这里结合wiki中最后推导到的一个等式,可用使用sagemath先定义一个x,并且x的计算是在模n的情况下的计算结果。ctfwiki的代码思路如下:
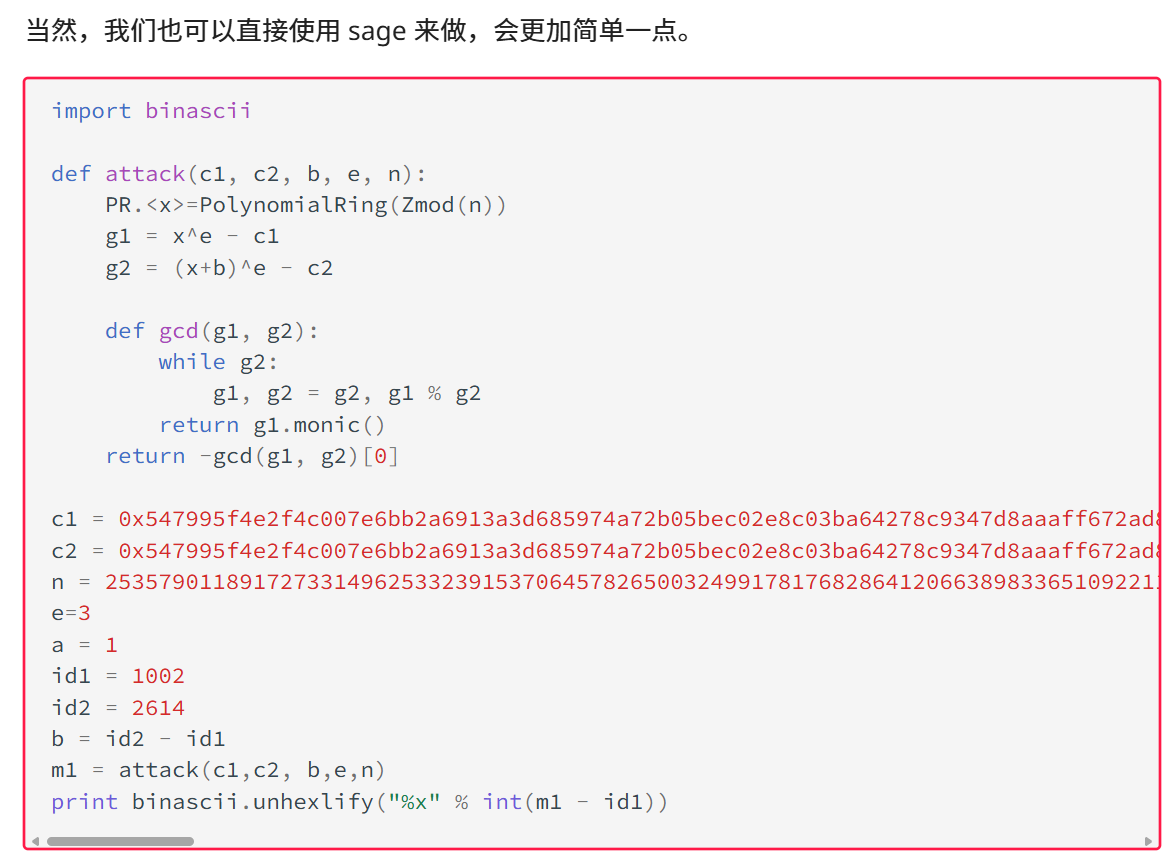
可以看到:利用sagemath中的语法定义x为在模n下的计算方式。
然后再列出数学的等式,g1和g2。我们把相关消息消息差值detal定义为hash(7)-hash(307),然后利用欧几里函数计算得到m1+hash(307),所以最后计算得到得就是m1+hash(307),最后将得到得计算结果变为整数数据然后利用long_to_bytes函数将其转化为字节数据。
#sagemath
import hashlib
from Crypto.Util.number import getPrime, bytes_to_long,long_to_bytes
def hash(x):
return int(hashlib.md5(str(x).encode()).hexdigest(), 16)
def attack(c1, c2, b, e, n):
PR.<x>=PolynomialRing(Zmod(n))
g1 = x^e - c1
g2 = (x+b)^e - c2
def gcd(g1, g2):
while g2:
g1, g2 = g2, g1 % g2
return g1.monic()
return -gcd(g1, g2)[0]
c1 = 41973910895747673899187679417443865074160589754180118442365040608786257167532976519645413349472355652086604920132172274308809002827286937134629295632868623764934042989648498006706284984313078230848738989331579140105876643369041029438708179499450424414752031366276378743595588425043730563346092854896545408366
c2 = 41973912583926901518444642835111314526720967879172223986535984124576403651553273447618087600591347032422378272332279802860926604693828116337548053006928860031338938935746179912330961194768693506712533420818446672613053888256943921222915644107389736912059397747390472331492265060448066180414639931364582445814
n = 100885785256342169056765112203447042910886647238787490462506364977429519290706204521984596783537199842140535823208433284571495132415960381175163434675775328905396713032321690195499705998621049971024487732085874710868565606249892231863632731481840542506411757024315315311788336796336407286355303887021285839839
e=3
id1 = hash(307)
id2 = hash(7)
b = id2 - id1
m1 = attack(c1,c2, b,e,n)
print(long_to_bytes(int(m1-hash(307))))
#TGCTF{RS4_Tw1nZ_d0You_th1nk_ItS_fun_2win?!!!1111111111}
这道题目让我学到了rsa得新的攻击方法,也许之后对于e很小并且给出的密文中有c1和c2之间使用同一个n加密的情况,可以尝试这种方法。
>
3.宝宝rsa
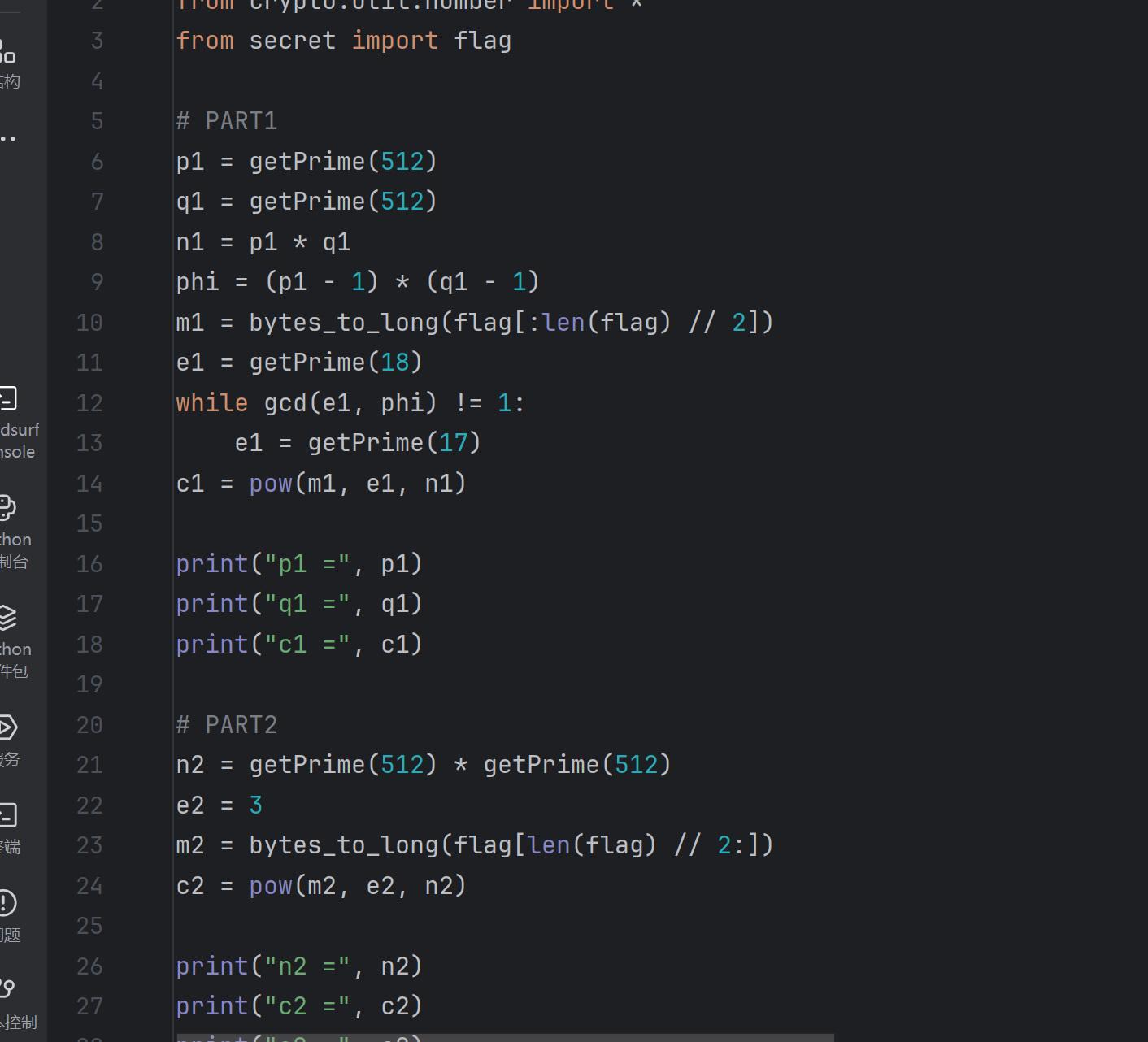
可以看到明文被拆开成两部分进行分别加密,通过进行代码分析,可以知道:
part1是把第一段从18位的密文里面取出一个素数然后与phi判断是不是属于跟phi互质的素数,不是就再取一位17位的素数继续进行如上的判断直到找到一个跟phi互质的e再进行加密,这里猜测需要进行爆破,而且是没有现成的脚本的。
part2的部分是把第二部分进行e=3的加密,这里由于e很小,而且中间的部分没作什么特殊处理,属于小e攻击的一种,使用之前存的小e攻击的脚本进行解密就可以。
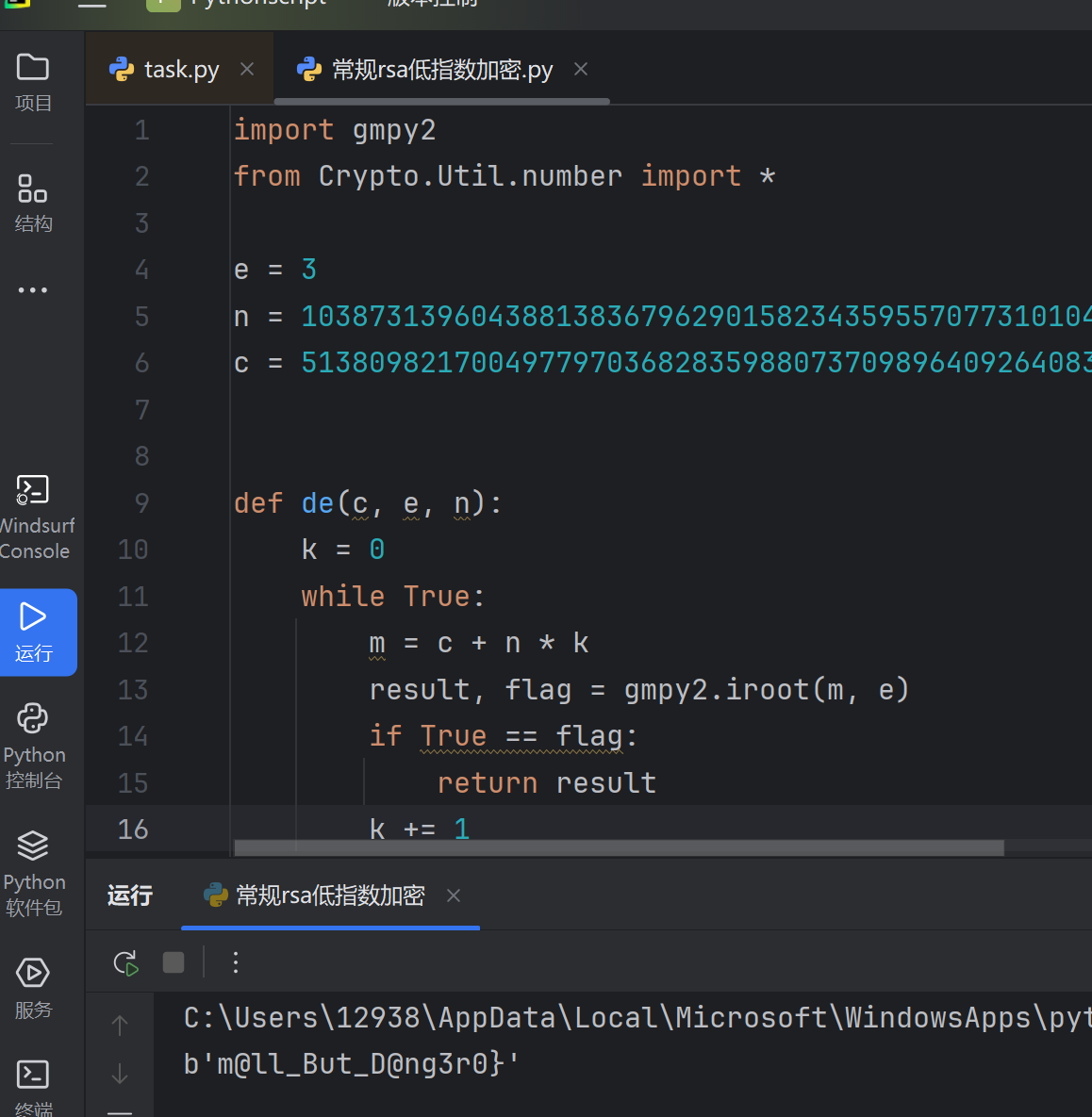
然后再对part1进行爆破解密:由于原来的函数getprime()函数是随机生成的一个素数,在进行爆破的时候不能在用它来取素数然后进行验证,因为一是有可能取到同样的,然后就是时间花销会增大(因为我踩了这个坑)。所以这里我们的思路就是先生成一个17位长的所以素数的列表和18位长所有素数的列表,然后把两者拼接在一起,然后从中取数进行验证,先验证是否跟phi互质,互质之后求出d然后变成byte类型然后对比前缀是否位“TGCTF{”,如果两个都对的上就输出这个字符串然后拼接提交。
from math import gcd
from Crypto.Util.number import long_to_bytes, inverse
import sympy
p1 = 8362851990079664018649774360159786938757293294328116561219351503022492961843907118845919317399785168488103775809531198339213009936918460080250107807031483 # 替换为实际 p1
q1 = 8312546034426788223492083178829355192676175323324230533451989649056072814335528263136523605276378801682321623998646291206494179416941978672637426346496531 # 替换为实际 q1
c1 = 39711973075443303473292859404026809299317446021917391206568511014894789946819103680496756934914058521250438186214943037578346772475409633145435232816799913236259074769958139045997486622505579239448395807857034154142067866860431132262060279168752474990452298895511880964765819538256786616223902867436130100322 # 替换为实际 c1
n1 = p1 * q1
phi = (p1 - 1) * (q1 - 1)
def generate_prime_candidates():
primes_17 = list(sympy.primerange(2 ** 16 + 1, 2 ** 17))
primes_18 = list(sympy.primerange(2 ** 17 + 1, 2 ** 18))
return primes_17 + primes_18
e_candidates = generate_prime_candidates()
found = False
for e in e_candidates:
if gcd(e, phi) != 1:
continue
try:
d = inverse(e, phi)
except ValueError:
continue
m = pow(c1, d, n1)
m_bytes = long_to_bytes(m)
if m_bytes.startswith(b'TGCTF{'):
print(f"e = {e}")
print(f"{m_bytes}m@ll_But_D@ng3r0"+'}')
found = True
break
if not found:
print("not found")
# Output:TGCTF{!!3xP_Is_Sm@ll_But_D@ng3r0}
这道题目并没有附件,而是直接给出了数据。
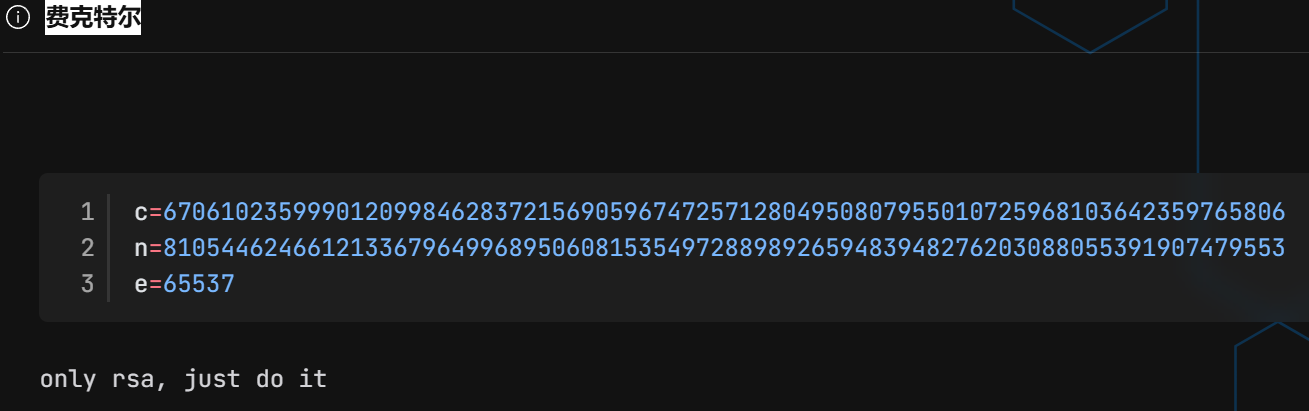
根据题目的音译为factor,可以知道这是叫我们分解n的意思。

可以看到分解成了多个n,我也是第一次看到这个分解成多个素数的n,然后去搜一下发现,当n分解为多个素数的时候一种的接触思路是两两为一组进行尝试解密成明文,还有一种就是n既然扩展为p1p2p3...,那么phi也应该扩展为(p1-1)(p2-1)(p3-1)...,本来准备对两种都进行尝试一下的时候,我发现用后面那一种的解密方法就已经直接解出了。
from Crypto.Util.number import inverse, long_to_bytes
p=[113, 18251,2001511,214168842768662180574654641,916848439436544911290378588839845528581]
c=670610235999012099846283721569059674725712804950807955010725968103642359765806
n=810544624661213367964996895060815354972889892659483948276203088055391907479553
e=65537
phi=1
for i in p:
phi*=(i-1)
d=inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))
#from Crypto.Util.number import inverse, long_to_bytes
p=[113, 18251,2001511,214168842768662180574654641,916848439436544911290378588839845528581]
c=670610235999012099846283721569059674725712804950807955010725968103642359765806
n=810544624661213367964996895060815354972889892659483948276203088055391907479553
e=65537
phi=1
for i in p:
phi*=(i-1)
d=inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))
#from Crypto.Util.number import inverse, long_to_bytes
p=[113, 18251,2001511,214168842768662180574654641,916848439436544911290378588839845528581]
c=670610235999012099846283721569059674725712804950807955010725968103642359765806
n=810544624661213367964996895060815354972889892659483948276203088055391907479553
e=65537
phi=1
for i in p:
phi*=(i-1)
d=inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))
#TGCTF{f4888_6abdc_9c2bd_9036bb}
这个题目是一道典型的rsa多个nc的加密。
下载txt文件打开可以看到如下信息。
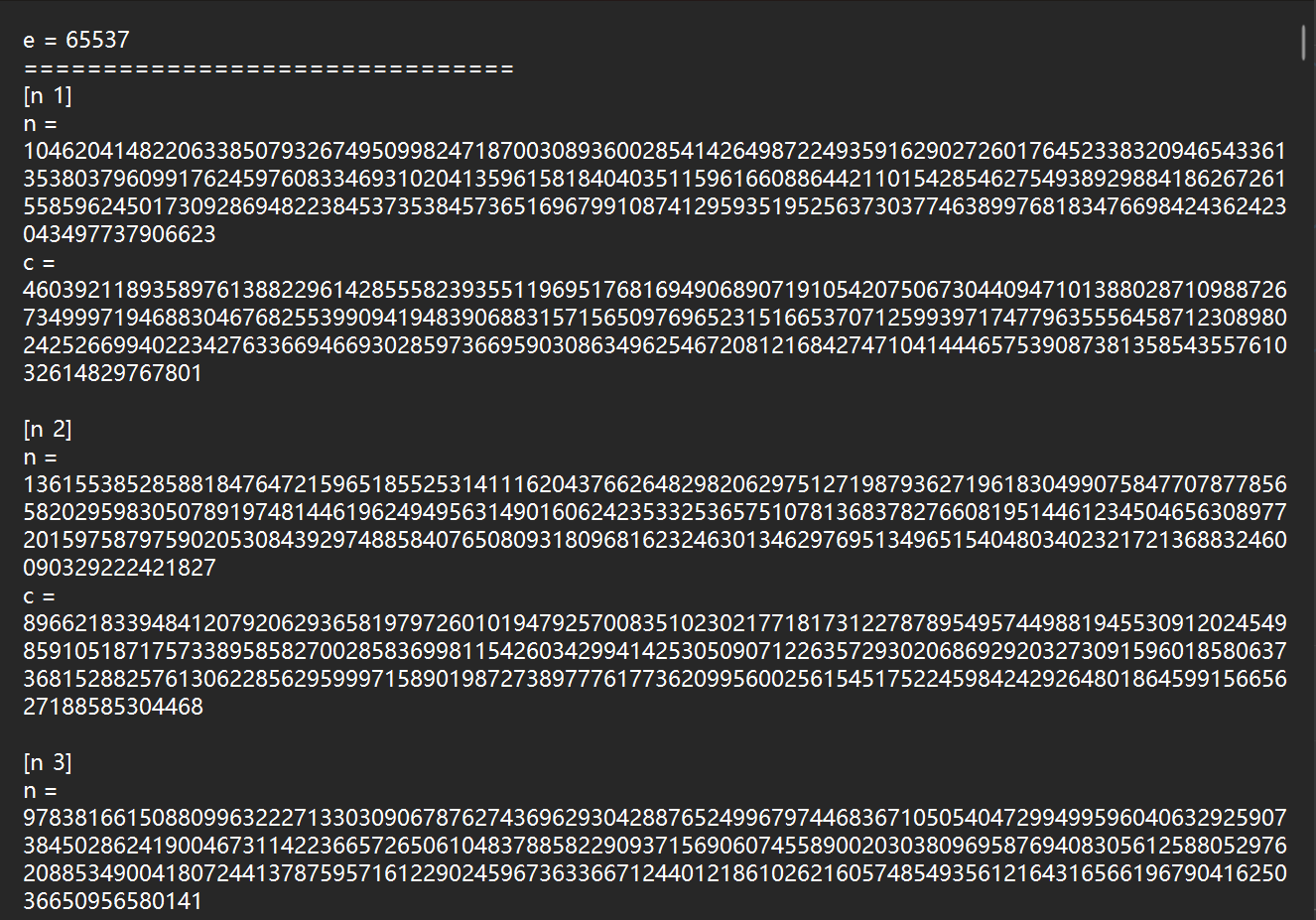
这里给了60组的n和c。原来就是利用欧几里德算法求出多组n之间公用的p值,从而求出q和phi,最后求出d,然后找到求到出这个p的最后那一组的序号,使用这个p对这一组进行解密。
这里给出求公共的p和其最后一组的序号的代码,因为要填入60组数据,所以这里不再累人了。
from gmpy2 import *
n=[n0,,n1,n2...,n59]
for i in range(len(n)):
for j in range(len(n)):
if(i!=j):
if(gcd(n[i],n[j])!=1): #对不同的n进行 欧几德得 算法,以求出最大公约数
print(i,j)
print("p =",gcd(n[i],n[j]))
最后可以找到公用的p和求出这个公用的p的最后一组的序号,然后进行解密就可以了。
原理是这样将,实际上进行爆破的时候发现有一堆的nc都可以求出同样的,如下:
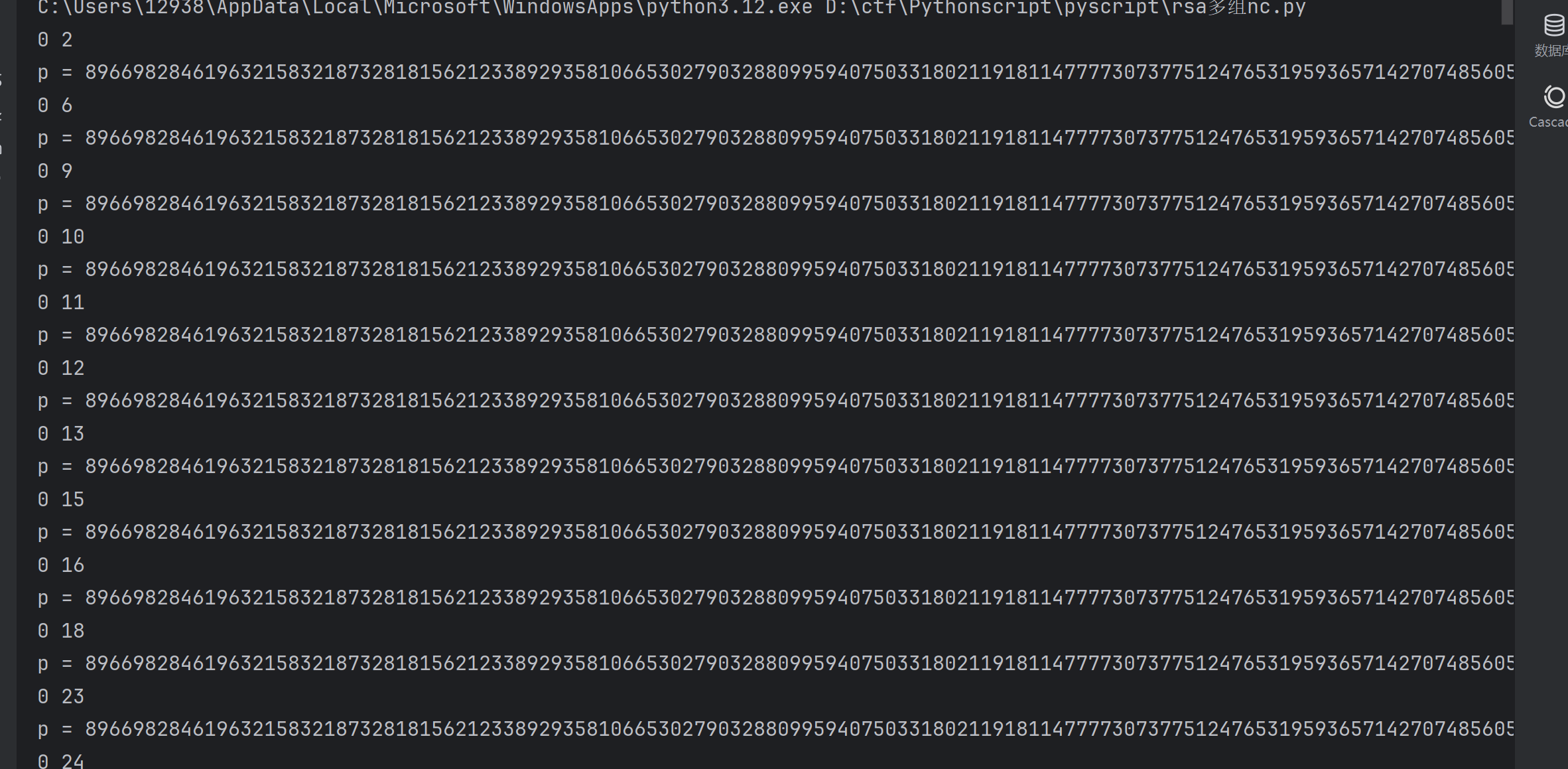
意思也就是说:其实不需要复制60份,最少是复制3组进去就可以求出flag,题目提示的也是这一点。
所以我们把0下标联立求出的p值跟0组对于的c值进行rsa解密得到如下:
from Crypto.Util.number import inverse, long_to_bytes
c=46039211893589761388229614285558239355119695176816949068907191054207506730440947101388028710988726734999719468830467682553990941948390688315715650976965231516653707125993971747796355564587123089802425266994022342763366946693028597366959030863496254672081216842747104144465753908738135854355761032614829767801
n=104620414822063385079326749509982471870030893600285414264987224935916290272601764523383209465433613538037960991762459760833469310204135961581840403511596166088644211015428546275493892988418626726155859624501730928694822384537353845736516967991087412959351952563730377463899768183476698424362423043497737906623
p=8966982846196321583218732818156212338929358106653027903288099594075033180211918114777730737751247653195936571427074856051307498770294940971178276714212171
e = 65537
q=n//p
phi=(p-1)*(q-1)
d=inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))
#TGCTF{ExcePt10n4lY0u_Fl4gF0rY0u_555b0nus}
就可以得到flag了。
Reverse
下载文件解压得到如下的文件:
尽心DIE扫描一下文件看看。
看到是64位的程序,放入IDA64分析一下。
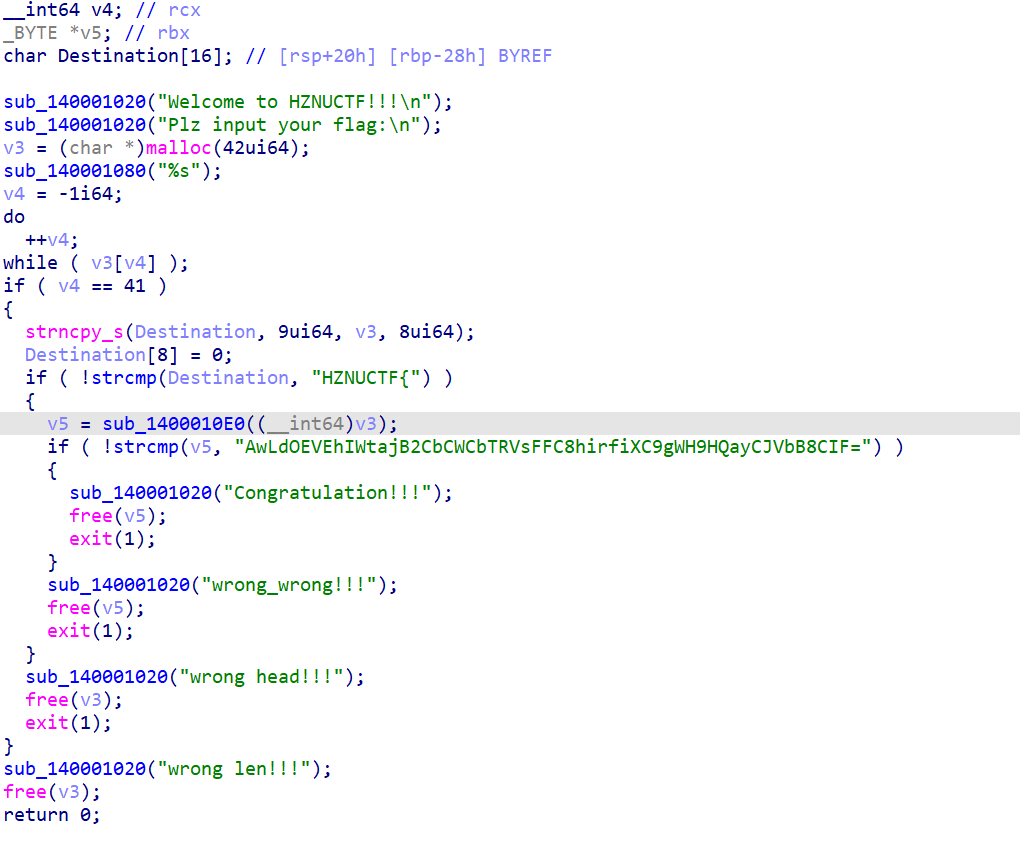
主函数的大致逻辑就是:
- 先把我们输入的字符串存储在v3中,IDA的错误分析导致scanf并未正常显示,不过猜也猜到到是存在v3中,进行动态调试就可以看到是存在v3之中。
- 之后会把我们输入的字符串的前缀给复制给destination然后进行对比,如果不对就直接不进行如下判断,如果符合就v3原封不动地进入下面的函数进行自定义的base64的编码,这里进入其函数看看。

 可以看到表和索引规则都变了,索引规则总结起来就是把三个字符变成四个字符的值的时候,对六位二进制还进行一个+24mod64的操作,这里我的思路不具备效率,所以这里采用官方wp进行解密。
可以看到表和索引规则都变了,索引规则总结起来就是把三个字符变成四个字符的值的时候,对六位二进制还进行一个+24mod64的操作,这里我的思路不具备效率,所以这里采用官方wp进行解密。- 我原本的思路是直接逆向,官方的wp则是把base64表进行偏移+24,让其恢复成原来的索引规则的模样,这样就可以进行cyberchef的梭哈了。
脚本如下:
str1="GLp/+Wn7uqX8FQ2JDR1c0M6U53sjBwyxglmrCVdSThAfEOvPHaYZNzo4ktK9iebI"
for i in range(24,len(str1)+24):
print(str1[i%64],end='')
#53sjBwyxglmrCVdSThAfEOvPHaYZNzo4ktK9iebIGLp/+Wn7uqX8FQ2JDR1c0M6U
然后放入cyberchef里面梭哈:
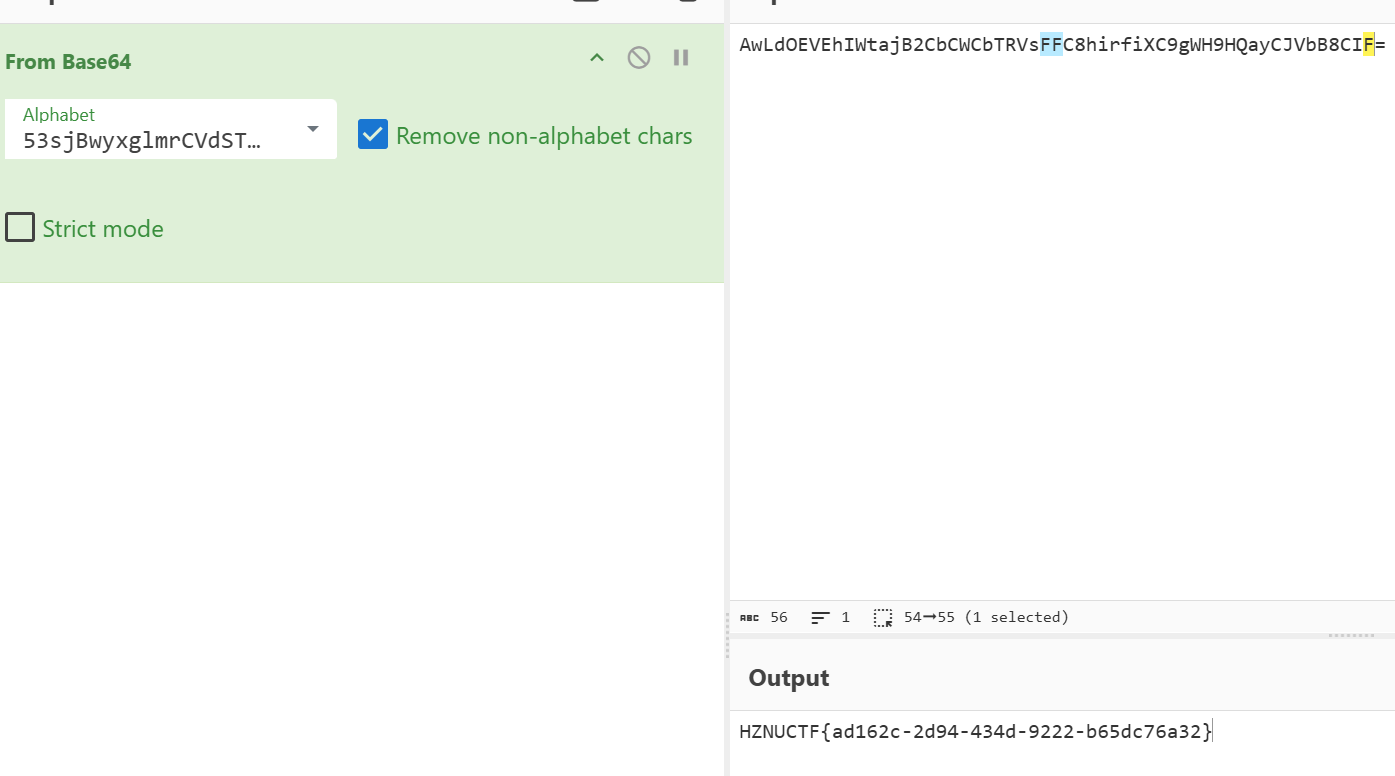
得到flag:HZNUCTF{ad162c-2d94-434d-9222-b65dc76a32}
看到题目如下:
不知道算不算提示,感觉跟misc没有屁关系,把文件进行DIE的扫描。
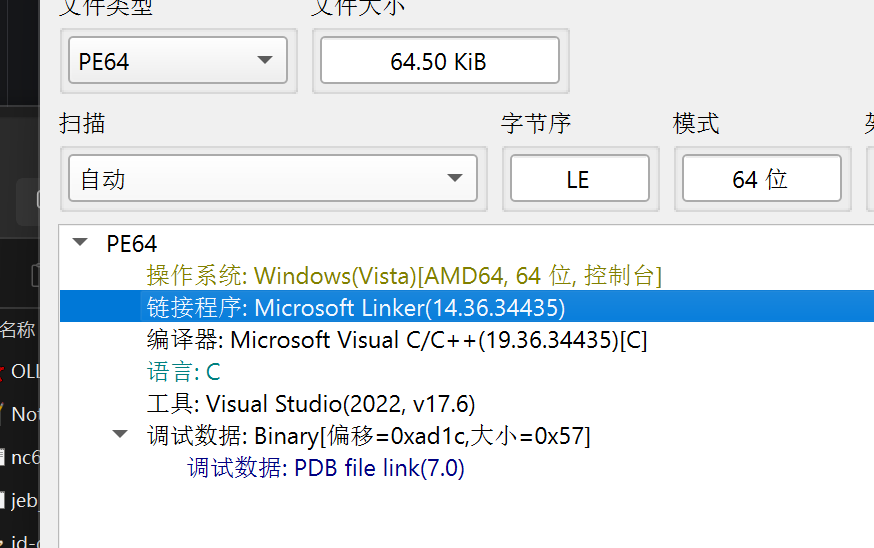
关键信息是64位,所以放入IDA64进行分析。

进入到主函数如上,进行分析发现:
第一段循环的时候,是把我们输入的字符串每四个四个字符处理成一个无符号的整数,因为字符转成数据都是无符号的,处理成整数字节之后进入到下面的sub_7FF781831212()函数进行处理,然后对我们8个无符号的整形数据每两个两个处理,处理六次。然后我们进入到下面的加密函数看看。
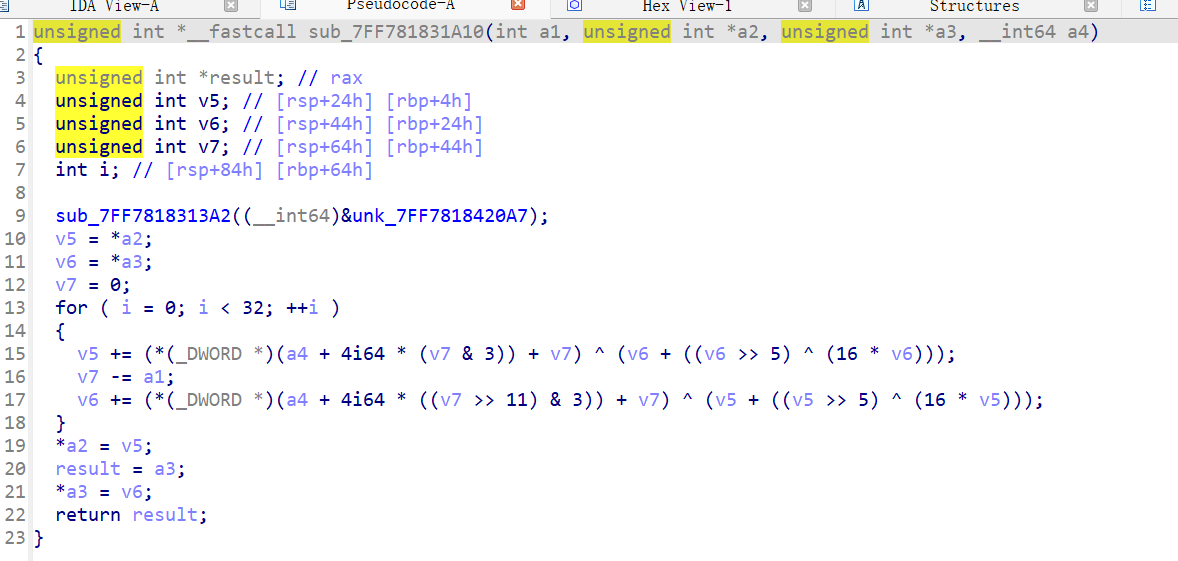
在sub_7FF781831212()函数中,我们进行代码分析确定逆向操作,由于两个都是异或操作所以异或符号的前后连个部分里面的是照抄的,接着由于,v6的处理会用到处理过的v5,所以在逆向操作是把v6的操作提前,然后再进行v5的逆向操作,由于是一种1根2异或存入1,2跟1'异或存入2,然后2'跟3异或存入2变成2'',类似这种的累层异或,最后解密也就要从最后一个先开始进行解密然后反复异或从而解到第一个,所以从末尾到前面的逆向操作的带代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
void decrypt_pair(uint32_t *v5, uint32_t *v6, int *key, int a1) {
uint32_t orig_v5 = *v5;
uint32_t orig_v6 = *v6;
int sum = -a1 * 32; // Sum初始化,加密后为-32*a1
for (int i = 0; i < 32; i++) {
uint32_t temp = (key[(sum >> 11) & 3] + sum) ^ (orig_v5 + ((orig_v5 >> 5) ^ (orig_v5 * 16)));
orig_v6 -= temp;
sum += a1;
temp = (key[sum & 3] + sum) ^ (orig_v6 + ((orig_v6 >> 5) ^ (orig_v6 * 16)));
orig_v5 -= temp;
}
*v5 = orig_v5;
*v6 = orig_v6;
}
int main() {
int key[4];
srand(0x7E8);
for (int i = 0; i < 4; i++) {
key[i] = rand();
}
uint32_t encrypted[] = {
0x8CCB2324, 0x09A7741A, 0xFB3C678D, 0xF6083A79,
0xF1CC241B, 0x39FA59F2, 0xF2ABE1CC, 0x17189F72
};
// 假设正确的cipher是XTEA的delta值0x9E3779B9
int a1 = 0x9E3779B9;
// 逆序处理每对
for (int k = 6; k >= 0; k--) {
decrypt_pair(&encrypted[k], &encrypted[k + 1], key, a1);
}
// 转换为字符
char flag[33] = {0};
for (int i = 0; i < 8; i++) {
flag[i * 4 + 0] = (encrypted[i] >> 24) & 0xFF;
flag[i * 4 + 1] = (encrypted[i] >> 16) & 0xFF;
flag[i * 4 + 2] = (encrypted[i] >> 8) & 0xFF;
flag[i * 4 + 3] = encrypted[i] & 0xFF;
}
printf("Flag: %s\n", flag);
return 0;
}
//Flag: HZNUCTF{ae6-9f57-4b74-b423-98eb}
所以得到了flag的结果。
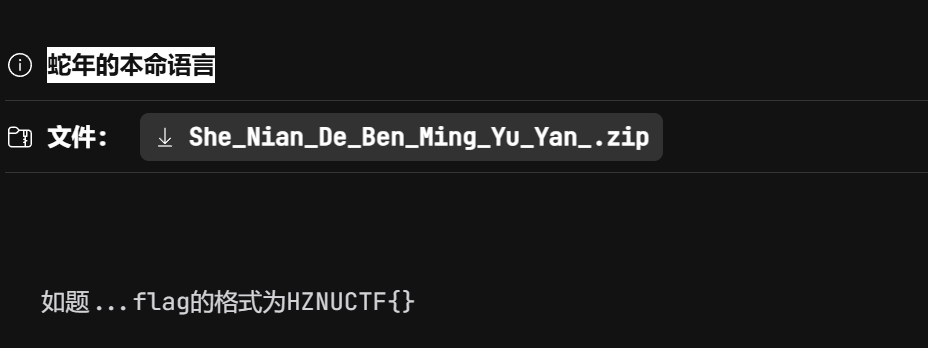
下载之后解压看到图标是pyinstaller打包的exe文件,然后把其用用pyinstxtractor解包。
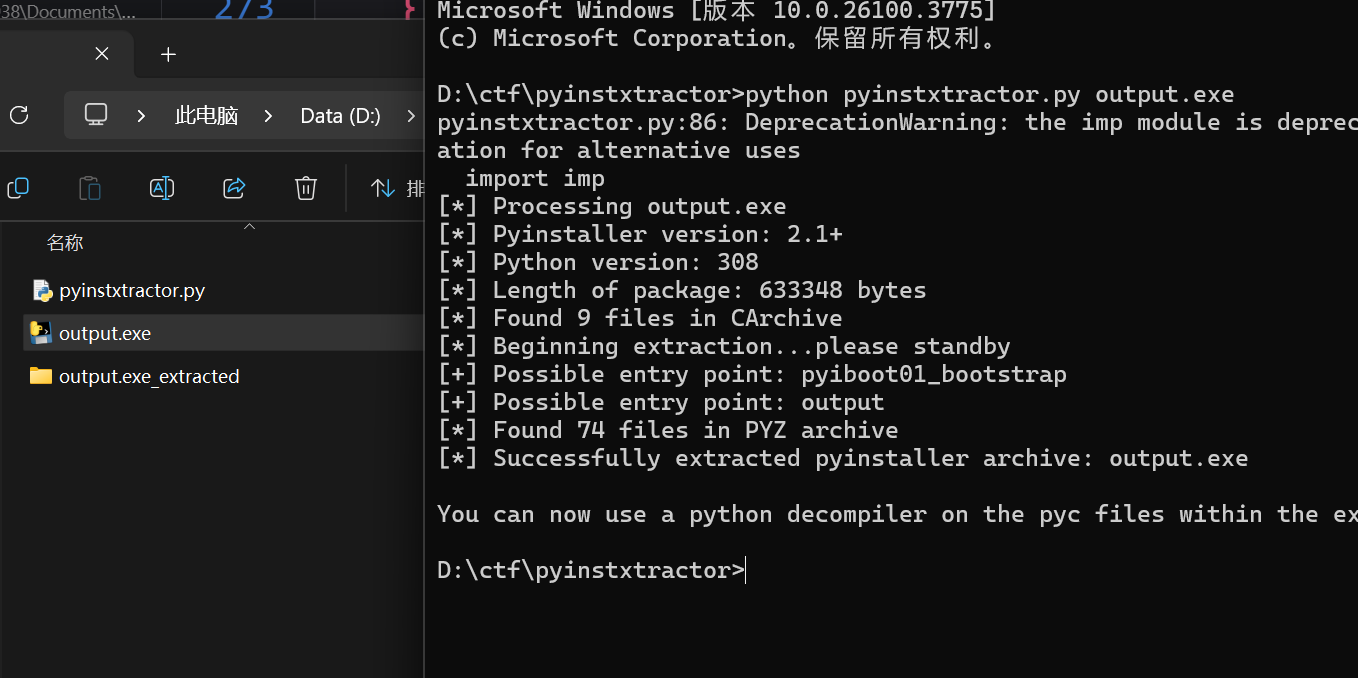
把解包之后的文件解压,然后把pyc利用uncompyle6反编译成py文件。但这里用pycdc也可以反汇编出大部分的原代码,只有一小部分对不上。
源代码如下:
# uncompyle6 version 3.9.2
# Python bytecode version base 3.8.0 (3413)
# Decompiled from: Python 3.8.10 (tags/v3.8.10:3d8993a, May 3 2021, 11:48:03) [MSC v.1928 64 bit (AMD64)]
# Embedded file name: output.py
from collections import Counter
print("Welcome to HZNUCTF!!!")
print("Plz input the flag:")
ooo0oOoooOOO0 = input()
oOO0OoOoo000 = Counter(ooo0oOoooOOO0)
O0o00 = "".join((str(oOO0OoOoo000[oOooo0OOO]) for oOooo0OOO in ))
print("ans1: ", end="")
print(O0o00)
if O0o00 != "111111116257645365477364777645752361":
print("wrong_wrong!!!")
exit(1)
iiIII = ""
for oOooo0OOO in ooo0oOoooOOO0:
if oOO0OoOoo000[oOooo0OOO] > 0:
iiIII += oOooo0OOO + str(oOO0OoOoo000[oOooo0OOO])
oOO0OoOoo000[oOooo0OOO] = 0
else:
i11i1Iii1I1 = [ord(oOooo0OOO) for oOooo0OOO in iiIII]
ii1iIi1i11i = [
7 * i11i1Iii1I1[0] == 504,
9 * i11i1Iii1I1[0] - 5 * i11i1Iii1I1[1] == 403,
2 * i11i1Iii1I1[0] - 5 * i11i1Iii1I1[1] + 10 * i11i1Iii1I1[2] == 799,
3 * i11i1Iii1I1[0] + 8 * i11i1Iii1I1[1] + 15 * i11i1Iii1I1[2] + 20 * i11i1Iii1I1[3] == 2938,
5 * i11i1Iii1I1[0] + 15 * i11i1Iii1I1[1] + 20 * i11i1Iii1I1[2] - 19 * i11i1Iii1I1[3] + 1 * i11i1Iii1I1[4] == 2042,
7 * i11i1Iii1I1[0] + 1 * i11i1Iii1I1[1] + 9 * i11i1Iii1I1[2] - 11 * i11i1Iii1I1[3] + 2 * i11i1Iii1I1[4] + 5 * i11i1Iii1I1[5] == 1225,
11 * i11i1Iii1I1[0] + 22 * i11i1Iii1I1[1] + 33 * i11i1Iii1I1[2] + 44 * i11i1Iii1I1[3] + 55 * i11i1Iii1I1[4] + 66 * i11i1Iii1I1[5] - 77 * i11i1Iii1I1[6] == 7975,
21 * i11i1Iii1I1[0] + 23 * i11i1Iii1I1[1] + 3 * i11i1Iii1I1[2] + 24 * i11i1Iii1I1[3] - 55 * i11i1Iii1I1[4] + 6 * i11i1Iii1I1[5] - 7 * i11i1Iii1I1[6] + 15 * i11i1Iii1I1[7] == 229,
2 * i11i1Iii1I1[0] + 26 * i11i1Iii1I1[1] + 13 * i11i1Iii1I1[2] + 0 * i11i1Iii1I1[3] - 65 * i11i1Iii1I1[4] + 15 * i11i1Iii1I1[5] + 29 * i11i1Iii1I1[6] + 1 * i11i1Iii1I1[7] + 20 * i11i1Iii1I1[8] == 2107,
10 * i11i1Iii1I1[0] + 7 * i11i1Iii1I1[1] + -9 * i11i1Iii1I1[2] + 6 * i11i1Iii1I1[3] + 7 * i11i1Iii1I1[4] + 1 * i11i1Iii1I1[5] + 22 * i11i1Iii1I1[6] + 21 * i11i1Iii1I1[7] - 22 * i11i1Iii1I1[8] + 30 * i11i1Iii1I1[9] == 4037,
15 * i11i1Iii1I1[0] + 59 * i11i1Iii1I1[1] + 56 * i11i1Iii1I1[2] + 66 * i11i1Iii1I1[3] + 7 * i11i1Iii1I1[4] + 1 * i11i1Iii1I1[5] - 122 * i11i1Iii1I1[6] + 21 * i11i1Iii1I1[7] + 32 * i11i1Iii1I1[8] + 3 * i11i1Iii1I1[9] - 10 * i11i1Iii1I1[10] == 4950,
13 * i11i1Iii1I1[0] + 66 * i11i1Iii1I1[1] + 29 * i11i1Iii1I1[2] + 39 * i11i1Iii1I1[3] - 33 * i11i1Iii1I1[4] + 13 * i11i1Iii1I1[5] - 2 * i11i1Iii1I1[6] + 42 * i11i1Iii1I1[7] + 62 * i11i1Iii1I1[8] + 1 * i11i1Iii1I1[9] - 10 * i11i1Iii1I1[10] + 11 * i11i1Iii1I1[11] == 12544,
23 * i11i1Iii1I1[0] + 6 * i11i1Iii1I1[1] + 29 * i11i1Iii1I1[2] + 3 * i11i1Iii1I1[3] - 3 * i11i1Iii1I1[4] + 63 * i11i1Iii1I1[5] - 25 * i11i1Iii1I1[6] + 2 * i11i1Iii1I1[7] + 32 * i11i1Iii1I1[8] + 1 * i11i1Iii1I1[9] - 10 * i11i1Iii1I1[10] + 11 * i11i1Iii1I1[11] - 12 * i11i1Iii1I1[12] == 6585,
223 * i11i1Iii1I1[0] + 6 * i11i1Iii1I1[1] - 29 * i11i1Iii1I1[2] - 53 * i11i1Iii1I1[3] - 3 * i11i1Iii1I1[4] + 3 * i11i1Iii1I1[5] - 65 * i11i1Iii1I1[6] + 0 * i11i1Iii1I1[7] + 36 * i11i1Iii1I1[8] + 1 * i11i1Iii1I1[9] - 15 * i11i1Iii1I1[10] + 16 * i11i1Iii1I1[11] - 18 * i11i1Iii1I1[12] + 13 * i11i1Iii1I1[13] == 6893,
29 * i11i1Iii1I1[0] + 13 * i11i1Iii1I1[1] - 9 * i11i1Iii1I1[2] - 93 * i11i1Iii1I1[3] + 33 * i11i1Iii1I1[4] + 6 * i11i1Iii1I1[5] + 65 * i11i1Iii1I1[6] + 1 * i11i1Iii1I1[7] - 36 * i11i1Iii1I1[8] + 0 * i11i1Iii1I1[9] - 16 * i11i1Iii1I1[10] + 96 * i11i1Iii1I1[11] - 68 * i11i1Iii1I1[12] + 33 * i11i1Iii1I1[13] - 14 * i11i1Iii1I1[14] == 1883,
69 * i11i1Iii1I1[0] + 77 * i11i1Iii1I1[1] - 93 * i11i1Iii1I1[2] - 12 * i11i1Iii1I1[3] + 0 * i11i1Iii1I1[4] + 0 * i11i1Iii1I1[5] + 1 * i11i1Iii1I1[6] + 16 * i11i1Iii1I1[7] + 36 * i11i1Iii1I1[8] + 6 * i11i1Iii1I1[9] + 19 * i11i1Iii1I1[10] + 66 * i11i1Iii1I1[11] - 8 * i11i1Iii1I1[12] + 38 * i11i1Iii1I1[13] - 16 * i11i1Iii1I1[14] + 15 * i11i1Iii1I1[15] == 8257,
23 * i11i1Iii1I1[0] + 2 * i11i1Iii1I1[1] - 3 * i11i1Iii1I1[2] - 11 * i11i1Iii1I1[3] + 12 * i11i1Iii1I1[4] + 24 * i11i1Iii1I1[5] + 1 * i11i1Iii1I1[6] + 6 * i11i1Iii1I1[7] + 14 * i11i1Iii1I1[8] - 0 * i11i1Iii1I1[9] + 1 * i11i1Iii1I1[10] + 68 * i11i1Iii1I1[11] - 18 * i11i1Iii1I1[12] + 68 * i11i1Iii1I1[13] - 26 * i11i1Iii1I1[14] + 15 * i11i1Iii1I1[15] - 16 * i11i1Iii1I1[16] == 5847,
24 * i11i1Iii1I1[0] + 0 * i11i1Iii1I1[1] - 1 * i11i1Iii1I1[2] - 15 * i11i1Iii1I1[3] + 13 * i11i1Iii1I1[4] + 4 * i11i1Iii1I1[5] + 16 * i11i1Iii1I1[6] + 67 * i11i1Iii1I1[7] + 146 * i11i1Iii1I1[8] - 50 * i11i1Iii1I1[9] + 16 * i11i1Iii1I1[10] + 6 * i11i1Iii1I1[11] - 1 * i11i1Iii1I1[12] + 69 * i11i1Iii1I1[13] - 27 * i11i1Iii1I1[14] + 45 * i11i1Iii1I1[15] - 6 * i11i1Iii1I1[16] + 17 * i11i1Iii1I1[17] == 18257,
25 * i11i1Iii1I1[0] + 26 * i11i1Iii1I1[1] - 89 * i11i1Iii1I1[2] + 16 * i11i1Iii1I1[3] + 19 * i11i1Iii1I1[4] + 44 * i11i1Iii1I1[5] + 36 * i11i1Iii1I1[6] + 66 * i11i1Iii1I1[7] - 150 * i11i1Iii1I1[8] - 250 * i11i1Iii1I1[9] + 166 * i11i1Iii1I1[10] + 126 * i11i1Iii1I1[11] - 11 * i11i1Iii1I1[12] + 690 * i11i1Iii1I1[13] - 207 * i11i1Iii1I1[14] + 46 * i11i1Iii1I1[15] + 6 * i11i1Iii1I1[16] + 7 * i11i1Iii1I1[17] - 18 * i11i1Iii1I1[18] == 12591,
5 * i11i1Iii1I1[0] + 26 * i11i1Iii1I1[1] + 8 * i11i1Iii1I1[2] + 160 * i11i1Iii1I1[3] + 9 * i11i1Iii1I1[4] - 4 * i11i1Iii1I1[5] + 36 * i11i1Iii1I1[6] + 6 * i11i1Iii1I1[7] - 15 * i11i1Iii1I1[8] - 20 * i11i1Iii1I1[9] + 66 * i11i1Iii1I1[10] + 16 * i11i1Iii1I1[11] - 1 * i11i1Iii1I1[12] + 690 * i11i1Iii1I1[13] - 20 * i11i1Iii1I1[14] + 46 * i11i1Iii1I1[15] + 6 * i11i1Iii1I1[16] + 7 * i11i1Iii1I1[17] - 18 * i11i1Iii1I1[18] + 19 * i11i1Iii1I1[19] == 52041,
29 * i11i1Iii1I1[0] - 26 * i11i1Iii1I1[1] + 0 * i11i1Iii1I1[2] + 60 * i11i1Iii1I1[3] + 90 * i11i1Iii1I1[4] - 4 * i11i1Iii1I1[5] + 6 * i11i1Iii1I1[6] + 6 * i11i1Iii1I1[7] - 16 * i11i1Iii1I1[8] - 21 * i11i1Iii1I1[9] + 69 * i11i1Iii1I1[10] + 6 * i11i1Iii1I1[11] - 12 * i11i1Iii1I1[12] + 69 * i11i1Iii1I1[13] - 20 * i11i1Iii1I1[14] - 46 * i11i1Iii1I1[15] + 65 * i11i1Iii1I1[16] + 0 * i11i1Iii1I1[17] - 1 * i11i1Iii1I1[18] + 39 * i11i1Iii1I1[19] - 20 * i11i1Iii1I1[20] == 20253,
45 * i11i1Iii1I1[0] - 56 * i11i1Iii1I1[1] + 10 * i11i1Iii1I1[2] + 650 * i11i1Iii1I1[3] - 900 * i11i1Iii1I1[4] + 44 * i11i1Iii1I1[5] + 66 * i11i1Iii1I1[6] - 6 * i11i1Iii1I1[7] - 6 * i11i1Iii1I1[8] - 21 * i11i1Iii1I1[9] + 9 * i11i1Iii1I1[10] - 6 * i11i1Iii1I1[11] - 12 * i11i1Iii1I1[12] + 69 * i11i1Iii1I1[13] - 2 * i11i1Iii1I1[14] - 406 * i11i1Iii1I1[15] + 651 * i11i1Iii1I1[16] + 2 * i11i1Iii1I1[17] - 10 * i11i1Iii1I1[18] + 69 * i11i1Iii1I1[19] - 0 * i11i1Iii1I1[20] + 21 * i11i1Iii1I1[21] == 18768,
555 * i11i1Iii1I1[0] - 6666 * i11i1Iii1I1[1] + 70 * i11i1Iii1I1[2] + 510 * i11i1Iii1I1[3] - 90 * i11i1Iii1I1[4] + 499 * i11i1Iii1I1[5] + 66 * i11i1Iii1I1[6] - 66 * i11i1Iii1I1[7] - 610 * i11i1Iii1I1[8] - 221 * i11i1Iii1I1[9] + 9 * i11i1Iii1I1[10] - 23 * i11i1Iii1I1[11] - 102 * i11i1Iii1I1[12] + 6 * i11i1Iii1I1[13] + 2050 * i11i1Iii1I1[14] - 406 * i11i1Iii1I1[15] + 665 * i11i1Iii1I1[16] + 333 * i11i1Iii1I1[17] + 100 * i11i1Iii1I1[18] + 609 * i11i1Iii1I1[19] + 777 * i11i1Iii1I1[20] + 201 * i11i1Iii1I1[21] - 22 * i11i1Iii1I1[22] == 111844,
1 * i11i1Iii1I1[0] - 22 * i11i1Iii1I1[1] + 333 * i11i1Iii1I1[2] + 4444 * i11i1Iii1I1[3] - 5555 * i11i1Iii1I1[4] + 6666 * i11i1Iii1I1[5] - 666 * i11i1Iii1I1[6] + 676 * i11i1Iii1I1[7] - 660 * i11i1Iii1I1[8] - 22 * i11i1Iii1I1[9] + 9 * i11i1Iii1I1[10] - 73 * i11i1Iii1I1[11] - 107 * i11i1Iii1I1[12] + 6 * i11i1Iii1I1[13] + 250 * i11i1Iii1I1[14] - 6 * i11i1Iii1I1[15] + 65 * i11i1Iii1I1[16] + 39 * i11i1Iii1I1[17] + 10 * i11i1Iii1I1[18] + 69 * i11i1Iii1I1[19] + 777 * i11i1Iii1I1[20] + 201 * i11i1Iii1I1[21] - 2 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] == 159029,
520 * i11i1Iii1I1[0] - 222 * i11i1Iii1I1[1] + 333 * i11i1Iii1I1[2] + 4 * i11i1Iii1I1[3] - 56655 * i11i1Iii1I1[4] + 6666 * i11i1Iii1I1[5] + 666 * i11i1Iii1I1[6] + 66 * i11i1Iii1I1[7] - 60 * i11i1Iii1I1[8] - 220 * i11i1Iii1I1[9] + 99 * i11i1Iii1I1[10] + 73 * i11i1Iii1I1[11] + 1007 * i11i1Iii1I1[12] + 7777 * i11i1Iii1I1[13] + 2500 * i11i1Iii1I1[14] + 6666 * i11i1Iii1I1[15] + 605 * i11i1Iii1I1[16] + 390 * i11i1Iii1I1[17] + 100 * i11i1Iii1I1[18] + 609 * i11i1Iii1I1[19] + 99999 * i11i1Iii1I1[20] + 210 * i11i1Iii1I1[21] + 232 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] - 24 * i11i1Iii1I1[24] == 2762025,
1323 * i11i1Iii1I1[0] - 22 * i11i1Iii1I1[1] + 333 * i11i1Iii1I1[2] + 4 * i11i1Iii1I1[3] - 55 * i11i1Iii1I1[4] + 666 * i11i1Iii1I1[5] + 666 * i11i1Iii1I1[6] + 66 * i11i1Iii1I1[7] - 660 * i11i1Iii1I1[8] - 220 * i11i1Iii1I1[9] + 99 * i11i1Iii1I1[10] + 3 * i11i1Iii1I1[11] + 100 * i11i1Iii1I1[12] + 777 * i11i1Iii1I1[13] + 2500 * i11i1Iii1I1[14] + 6666 * i11i1Iii1I1[15] + 605 * i11i1Iii1I1[16] + 390 * i11i1Iii1I1[17] + 100 * i11i1Iii1I1[18] + 609 * i11i1Iii1I1[19] + 9999 * i11i1Iii1I1[20] + 210 * i11i1Iii1I1[21] + 232 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] - 24 * i11i1Iii1I1[24] + 25 * i11i1Iii1I1[25] == 1551621,
777 * i11i1Iii1I1[0] - 22 * i11i1Iii1I1[1] + 6969 * i11i1Iii1I1[2] + 4 * i11i1Iii1I1[3] - 55 * i11i1Iii1I1[4] + 666 * i11i1Iii1I1[5] - 6 * i11i1Iii1I1[6] + 96 * i11i1Iii1I1[7] - 60 * i11i1Iii1I1[8] - 220 * i11i1Iii1I1[9] + 99 * i11i1Iii1I1[10] + 3 * i11i1Iii1I1[11] + 100 * i11i1Iii1I1[12] + 777 * i11i1Iii1I1[13] + 250 * i11i1Iii1I1[14] + 666 * i11i1Iii1I1[15] + 65 * i11i1Iii1I1[16] + 90 * i11i1Iii1I1[17] + 100 * i11i1Iii1I1[18] + 609 * i11i1Iii1I1[19] + 999 * i11i1Iii1I1[20] + 21 * i11i1Iii1I1[21] + 232 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] - 24 * i11i1Iii1I1[24] + 25 * i11i1Iii1I1[25] - 26 * i11i1Iii1I1[26] == 948348,
97 * i11i1Iii1I1[0] - 22 * i11i1Iii1I1[1] + 6969 * i11i1Iii1I1[2] + 4 * i11i1Iii1I1[3] - 56 * i11i1Iii1I1[4] + 96 * i11i1Iii1I1[5] - 6 * i11i1Iii1I1[6] + 96 * i11i1Iii1I1[7] - 60 * i11i1Iii1I1[8] - 20 * i11i1Iii1I1[9] + 99 * i11i1Iii1I1[10] + 3 * i11i1Iii1I1[11] + 10 * i11i1Iii1I1[12] + 707 * i11i1Iii1I1[13] + 250 * i11i1Iii1I1[14] + 666 * i11i1Iii1I1[15] + -9 * i11i1Iii1I1[16] + 90 * i11i1Iii1I1[17] + -2 * i11i1Iii1I1[18] + 609 * i11i1Iii1I1[19] + 0 * i11i1Iii1I1[20] + 21 * i11i1Iii1I1[21] + 2 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] - 24 * i11i1Iii1I1[24] + 25 * i11i1Iii1I1[25] - 26 * i11i1Iii1I1[26] + 27 * i11i1Iii1I1[27] == 777044,
177 * i11i1Iii1I1[0] - 22 * i11i1Iii1I1[1] + 699 * i11i1Iii1I1[2] + 64 * i11i1Iii1I1[3] - 56 * i11i1Iii1I1[4] - 96 * i11i1Iii1I1[5] - 66 * i11i1Iii1I1[6] + 96 * i11i1Iii1I1[7] - 60 * i11i1Iii1I1[8] - 20 * i11i1Iii1I1[9] + 99 * i11i1Iii1I1[10] + 3 * i11i1Iii1I1[11] + 10 * i11i1Iii1I1[12] + 707 * i11i1Iii1I1[13] + 250 * i11i1Iii1I1[14] + 666 * i11i1Iii1I1[15] + -9 * i11i1Iii1I1[16] + 0 * i11i1Iii1I1[17] + -2 * i11i1Iii1I1[18] + 69 * i11i1Iii1I1[19] + 0 * i11i1Iii1I1[20] + 21 * i11i1Iii1I1[21] + 222 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] - 224 * i11i1Iii1I1[24] + 25 * i11i1Iii1I1[25] - 26 * i11i1Iii1I1[26] + 27 * i11i1Iii1I1[27] - 28 * i11i1Iii1I1[28] == 185016,
77 * i11i1Iii1I1[0] - 2 * i11i1Iii1I1[1] + 6 * i11i1Iii1I1[2] + 6 * i11i1Iii1I1[3] - 96 * i11i1Iii1I1[4] - 9 * i11i1Iii1I1[5] - 6 * i11i1Iii1I1[6] + 96 * i11i1Iii1I1[7] - 0 * i11i1Iii1I1[8] - 20 * i11i1Iii1I1[9] + 99 * i11i1Iii1I1[10] + 3 * i11i1Iii1I1[11] + 10 * i11i1Iii1I1[12] + 707 * i11i1Iii1I1[13] + 250 * i11i1Iii1I1[14] + 666 * i11i1Iii1I1[15] + -9 * i11i1Iii1I1[16] + 0 * i11i1Iii1I1[17] + -2 * i11i1Iii1I1[18] + 9 * i11i1Iii1I1[19] + 0 * i11i1Iii1I1[20] + 21 * i11i1Iii1I1[21] + 222 * i11i1Iii1I1[22] + 23 * i11i1Iii1I1[23] - 224 * i11i1Iii1I1[24] + 26 * i11i1Iii1I1[25] - -58 * i11i1Iii1I1[26] + 27 * i11i1Iii1I1[27] - 2 * i11i1Iii1I1[28] + 29 * i11i1Iii1I1[29] == 130106]
if all(ii1iIi1i11i):
print("Congratulation!!!")
else:
print("wrong_wrong!!!")
# okay decompiling output.pyc
可以看到变量名字相当复杂,对其进行替换。
如下:
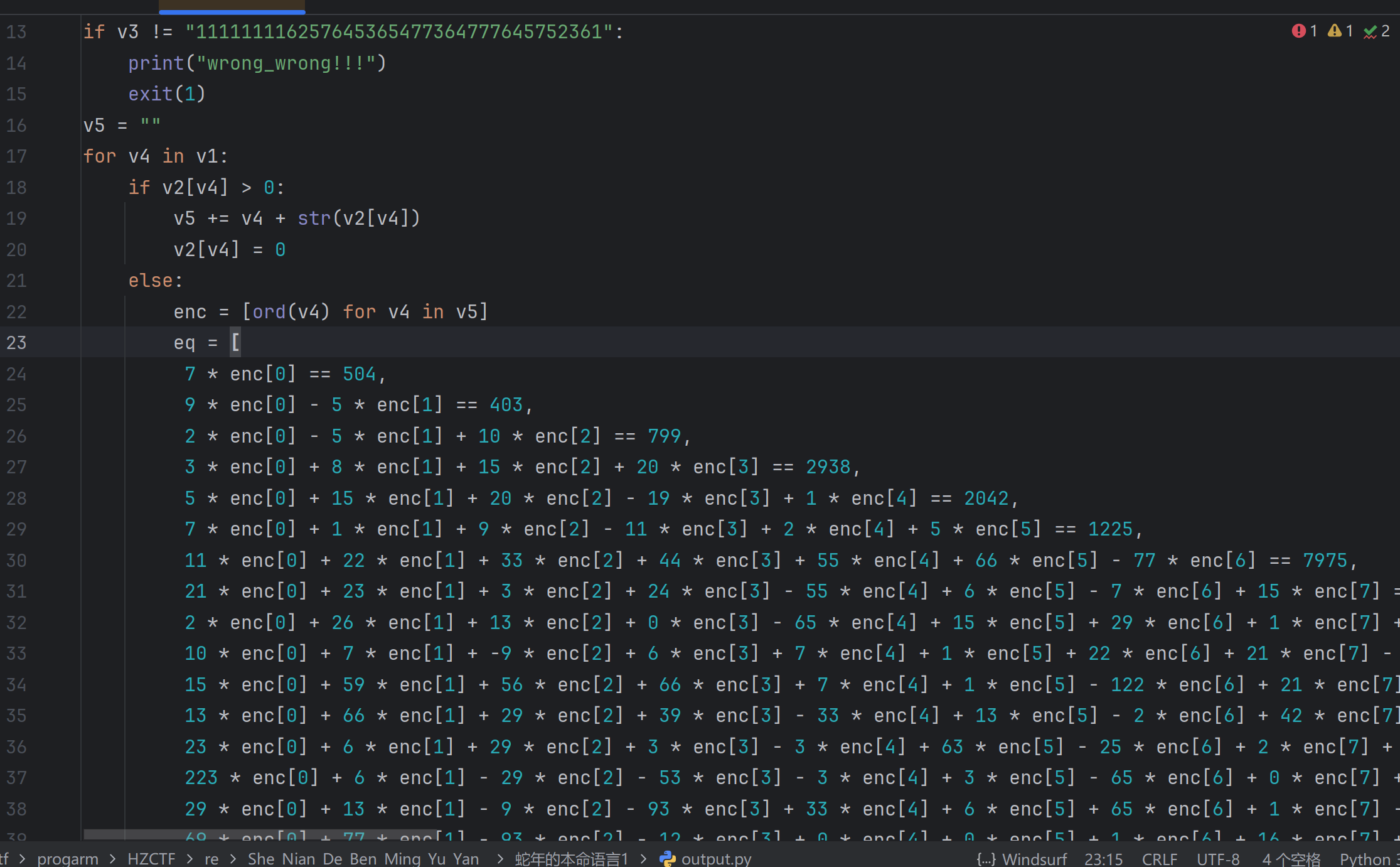
然后准备用sagemath语法进行求解。
因为这里面的表达式都是在enc里面的值,搜先在enc里面定义一堆变量,用于后续的求解方程组,然后再求解然后把方程式放入进去,然后用solve()函数进行求解,确定eq为方程式子,求的自变量为enc中的变量,然后使用字典的输出结果到rel里,然后方便输出具体的结果。
给出代码如下:
enc=[var(f'a{i}',domain='integer') for i in range(30)]
eq= [
7 * enc[0] == 504,
9 * enc[0] - 5 * enc[1] == 403,
2 * enc[0] - 5 * enc[1] + 10 * enc[2] == 799,
3 * enc[0] + 8 * enc[1] + 15 * enc[2] + 20 * enc[3] == 2938,
5 * enc[0] + 15 * enc[1] + 20 * enc[2] - 19 * enc[3] + 1 * enc[4] == 2042,
7 * enc[0] + 1 * enc[1] + 9 * enc[2] - 11 * enc[3] + 2 * enc[4] + 5 * enc[5] == 1225,
11 * enc[0] + 22 * enc[1] + 33 * enc[2] + 44 * enc[3] + 55 * enc[4] + 66 * enc[5] - 77 * enc[6] == 7975,
21 * enc[0] + 23 * enc[1] + 3 * enc[2] + 24 * enc[3] - 55 * enc[4] + 6 * enc[5] - 7 * enc[6] + 15 * enc[7] == 229,
2 * enc[0] + 26 * enc[1] + 13 * enc[2] + 0 * enc[3] - 65 * enc[4] + 15 * enc[5] + 29 * enc[6] + 1 * enc[7] + 20 * enc[8] == 2107,
10 * enc[0] + 7 * enc[1] + -9 * enc[2] + 6 * enc[3] + 7 * enc[4] + 1 * enc[5] + 22 * enc[6] + 21 * enc[7] - 22 * enc[8] + 30 * enc[9] == 4037,
15 * enc[0] + 59 * enc[1] + 56 * enc[2] + 66 * enc[3] + 7 * enc[4] + 1 * enc[5] - 122 * enc[6] + 21 * enc[7] + 32 * enc[8] + 3 * enc[9] - 10 * enc[10] == 4950,
13 * enc[0] + 66 * enc[1] + 29 * enc[2] + 39 * enc[3] - 33 * enc[4] + 13 * enc[5] - 2 * enc[6] + 42 * enc[7] + 62 * enc[8] + 1 * enc[9] - 10 * enc[10] + 11 * enc[11] == 12544,
23 * enc[0] + 6 * enc[1] + 29 * enc[2] + 3 * enc[3] - 3 * enc[4] + 63 * enc[5] - 25 * enc[6] + 2 * enc[7] + 32 * enc[8] + 1 * enc[9] - 10 * enc[10] + 11 * enc[11] - 12 * enc[12] == 6585,
223 * enc[0] + 6 * enc[1] - 29 * enc[2] - 53 * enc[3] - 3 * enc[4] + 3 * enc[5] - 65 * enc[6] + 0 * enc[7] + 36 * enc[8] + 1 * enc[9] - 15 * enc[10] + 16 * enc[11] - 18 * enc[12] + 13 * enc[13] == 6893,
29 * enc[0] + 13 * enc[1] - 9 * enc[2] - 93 * enc[3] + 33 * enc[4] + 6 * enc[5] + 65 * enc[6] + 1 * enc[7] - 36 * enc[8] + 0 * enc[9] - 16 * enc[10] + 96 * enc[11] - 68 * enc[12] + 33 * enc[13] - 14 * enc[14] == 1883,
69 * enc[0] + 77 * enc[1] - 93 * enc[2] - 12 * enc[3] + 0 * enc[4] + 0 * enc[5] + 1 * enc[6] + 16 * enc[7] + 36 * enc[8] + 6 * enc[9] + 19 * enc[10] + 66 * enc[11] - 8 * enc[12] + 38 * enc[13] - 16 * enc[14] + 15 * enc[15] == 8257,
23 * enc[0] + 2 * enc[1] - 3 * enc[2] - 11 * enc[3] + 12 * enc[4] + 24 * enc[5] + 1 * enc[6] + 6 * enc[7] + 14 * enc[8] - 0 * enc[9] + 1 * enc[10] + 68 * enc[11] - 18 * enc[12] + 68 * enc[13] - 26 * enc[14] + 15 * enc[15] - 16 * enc[16] == 5847,
24 * enc[0] + 0 * enc[1] - 1 * enc[2] - 15 * enc[3] + 13 * enc[4] + 4 * enc[5] + 16 * enc[6] + 67 * enc[7] + 146 * enc[8] - 50 * enc[9] + 16 * enc[10] + 6 * enc[11] - 1 * enc[12] + 69 * enc[13] - 27 * enc[14] + 45 * enc[15] - 6 * enc[16] + 17 * enc[17] == 18257,
25 * enc[0] + 26 * enc[1] - 89 * enc[2] + 16 * enc[3] + 19 * enc[4] + 44 * enc[5] + 36 * enc[6] + 66 * enc[7] - 150 * enc[8] - 250 * enc[9] + 166 * enc[10] + 126 * enc[11] - 11 * enc[12] + 690 * enc[13] - 207 * enc[14] + 46 * enc[15] + 6 * enc[16] + 7 * enc[17] - 18 * enc[18] == 12591,
5 * enc[0] + 26 * enc[1] + 8 * enc[2] + 160 * enc[3] + 9 * enc[4] - 4 * enc[5] + 36 * enc[6] + 6 * enc[7] - 15 * enc[8] - 20 * enc[9] + 66 * enc[10] + 16 * enc[11] - 1 * enc[12] + 690 * enc[13] - 20 * enc[14] + 46 * enc[15] + 6 * enc[16] + 7 * enc[17] - 18 * enc[18] + 19 * enc[19] == 52041,
29 * enc[0] - 26 * enc[1] + 0 * enc[2] + 60 * enc[3] + 90 * enc[4] - 4 * enc[5] + 6 * enc[6] + 6 * enc[7] - 16 * enc[8] - 21 * enc[9] + 69 * enc[10] + 6 * enc[11] - 12 * enc[12] + 69 * enc[13] - 20 * enc[14] - 46 * enc[15] + 65 * enc[16] + 0 * enc[17] - 1 * enc[18] + 39 * enc[19] - 20 * enc[20] == 20253,
45 * enc[0] - 56 * enc[1] + 10 * enc[2] + 650 * enc[3] - 900 * enc[4] + 44 * enc[5] + 66 * enc[6] - 6 * enc[7] - 6 * enc[8] - 21 * enc[9] + 9 * enc[10] - 6 * enc[11] - 12 * enc[12] + 69 * enc[13] - 2 * enc[14] - 406 * enc[15] + 651 * enc[16] + 2 * enc[17] - 10 * enc[18] + 69 * enc[19] - 0 * enc[20] + 21 * enc[21] == 18768,
555 * enc[0] - 6666 * enc[1] + 70 * enc[2] + 510 * enc[3] - 90 * enc[4] + 499 * enc[5] + 66 * enc[6] - 66 * enc[7] - 610 * enc[8] - 221 * enc[9] + 9 * enc[10] - 23 * enc[11] - 102 * enc[12] + 6 * enc[13] + 2050 * enc[14] - 406 * enc[15] + 665 * enc[16] + 333 * enc[17] + 100 * enc[18] + 609 * enc[19] + 777 * enc[20] + 201 * enc[21] - 22 * enc[22] == 111844,
1 * enc[0] - 22 * enc[1] + 333 * enc[2] + 4444 * enc[3] - 5555 * enc[4] + 6666 * enc[5] - 666 * enc[6] + 676 * enc[7] - 660 * enc[8] - 22 * enc[9] + 9 * enc[10] - 73 * enc[11] - 107 * enc[12] + 6 * enc[13] + 250 * enc[14] - 6 * enc[15] + 65 * enc[16] + 39 * enc[17] + 10 * enc[18] + 69 * enc[19] + 777 * enc[20] + 201 * enc[21] - 2 * enc[22] + 23 * enc[23] == 159029,
520 * enc[0] - 222 * enc[1] + 333 * enc[2] + 4 * enc[3] - 56655 * enc[4] + 6666 * enc[5] + 666 * enc[6] + 66 * enc[7] - 60 * enc[8] - 220 * enc[9] + 99 * enc[10] + 73 * enc[11] + 1007 * enc[12] + 7777 * enc[13] + 2500 * enc[14] + 6666 * enc[15] + 605 * enc[16] + 390 * enc[17] + 100 * enc[18] + 609 * enc[19] + 99999 * enc[20] + 210 * enc[21] + 232 * enc[22] + 23 * enc[23] - 24 * enc[24] == 2762025,
1323 * enc[0] - 22 * enc[1] + 333 * enc[2] + 4 * enc[3] - 55 * enc[4] + 666 * enc[5] + 666 * enc[6] + 66 * enc[7] - 660 * enc[8] - 220 * enc[9] + 99 * enc[10] + 3 * enc[11] + 100 * enc[12] + 777 * enc[13] + 2500 * enc[14] + 6666 * enc[15] + 605 * enc[16] + 390 * enc[17] + 100 * enc[18] + 609 * enc[19] + 9999 * enc[20] + 210 * enc[21] + 232 * enc[22] + 23 * enc[23] - 24 * enc[24] + 25 * enc[25] == 1551621,
777 * enc[0] - 22 * enc[1] + 6969 * enc[2] + 4 * enc[3] - 55 * enc[4] + 666 * enc[5] - 6 * enc[6] + 96 * enc[7] - 60 * enc[8] - 220 * enc[9] + 99 * enc[10] + 3 * enc[11] + 100 * enc[12] + 777 * enc[13] + 250 * enc[14] + 666 * enc[15] + 65 * enc[16] + 90 * enc[17] + 100 * enc[18] + 609 * enc[19] + 999 * enc[20] + 21 * enc[21] + 232 * enc[22] + 23 * enc[23] - 24 * enc[24] + 25 * enc[25] - 26 * enc[26] == 948348,
97 * enc[0] - 22 * enc[1] + 6969 * enc[2] + 4 * enc[3] - 56 * enc[4] + 96 * enc[5] - 6 * enc[6] + 96 * enc[7] - 60 * enc[8] - 20 * enc[9] + 99 * enc[10] + 3 * enc[11] + 10 * enc[12] + 707 * enc[13] + 250 * enc[14] + 666 * enc[15] + -9 * enc[16] + 90 * enc[17] + -2 * enc[18] + 609 * enc[19] + 0 * enc[20] + 21 * enc[21] + 2 * enc[22] + 23 * enc[23] - 24 * enc[24] + 25 * enc[25] - 26 * enc[26] + 27 * enc[27] == 777044,
177 * enc[0] - 22 * enc[1] + 699 * enc[2] + 64 * enc[3] - 56 * enc[4] - 96 * enc[5] - 66 * enc[6] + 96 * enc[7] - 60 * enc[8] - 20 * enc[9] + 99 * enc[10] + 3 * enc[11] + 10 * enc[12] + 707 * enc[13] + 250 * enc[14] + 666 * enc[15] + -9 * enc[16] + 0 * enc[17] + -2 * enc[18] + 69 * enc[19] + 0 * enc[20] + 21 * enc[21] + 222 * enc[22] + 23 * enc[23] - 224 * enc[24] + 25 * enc[25] - 26 * enc[26] + 27 * enc[27] - 28 * enc[28] == 185016,
77 * enc[0] - 2 * enc[1] + 6 * enc[2] + 6 * enc[3] - 96 * enc[4] - 9 * enc[5] - 6 * enc[6] + 96 * enc[7] - 0 * enc[8] - 20 * enc[9] + 99 * enc[10] + 3 * enc[11] + 10 * enc[12] + 707 * enc[13] + 250 * enc[14] + 666 * enc[15] + -9 * enc[16] + 0 * enc[17] + -2 * enc[18] + 9 * enc[19] + 0 * enc[20] + 21 * enc[21] + 222 * enc[22] + 23 * enc[23] - 224 * enc[24] + 26 * enc[25] - -58 * enc[26] + 27 * enc[27] - 2 * enc[28] + 29 * enc[29] == 130106]
rel = solve(eq,enc[:30],solution_dict=True)
for s in rel:
print([chr(s[v]) for v in enc[:30]])
#['H', '1', 'Z', '1', 'N', '1', 'U', '1', 'C', '1', 'T', '1', 'F', '1', '{', '1', 'a', '6', 'd', '2', '7', '5', 'f', '7', '-', '4', '6', '3', '}', '1']
上面是sage的脚本,的到运行输出之后的字符串是:H1Z1N1U1C1T1F1{1a6d275f7-463}1
这里我第一次理解为字符后面的数字是字符出现的次数,这句话确实是没错的,但我错误的理解为就是字符出现的位置就在其当前的位置上,实际上对比一开始的校验字符串:111111116257645365477364777645752361
可以看到出现了6次6,也就是说,实际上后面的数字也对应了其字符出现的位置。这是我比赛的时候没想到从而导致没解出的失败之处。
这里使用文本编辑攻击进行替换就可以解密了。
注意这里5和7的位置的值互换就好。
也可以写解密脚本,但是1可以先特殊处理一下,如下:
table= "625764536547736477764575236"
#'a', '6', 'd', '2', '7', '5', 'f', '7', '-', '4', '6', '3'
flag = 'HZNUCTF{'
for i in table:
if i=='6':
flag += 'a'
if i=='2':
flag += 'd'
if i=='5':
flag += '7'
if i=='7':
flag += 'f'
if i=='4':
flag += '-'
if i=='3':
flag += '6'
print(flag+"}")
#HZNUCTF{ad7fa-76a7-ff6a-fffa-7f7d6a}
解得flag为:HZNUCTF{ad7fa-76a7-ff6a-fffa-7f7d6a}
水果忍者(复现)
由于我对unity游戏文件的逆向知识知之甚少,所以这道题目的做法的过程我并不是很了解,官方wp里面写的工具和访问的文件的原由我都是在查找过资料之后才弄清楚的。这里主要涉及到的unity游戏文件的相关知识就是:
- Assembly-CSharp.dll的作用,这个文件在unity游戏中叫做程序集,其是游戏代码编译的逻辑单元,所有跟游戏主要的运行过程的代码都会跟其相关,因为那些一个个dll文件或者是exe文件都是经过这个文件之手所得到的,所以这个文件就相当于一个c语言exe文件的主函数一样的角色。
- 而unity游戏文件逆向的工具可能使用的是dnSpy或者ILSpy这两种工具进行反汇编,而dnSpy这个工具进行逆向的时候其会反映出这个unity文件之间的关系和类型,并且其可以通过对不同的变量双击从而跳转到不同的文件里的变量的对应的可能所在处。ILSpy也是反汇编的,其相对有的有点大概就是简洁和容易上手吧。还有一个可以获取游戏资产的工具AssetStudioGUI,这里不多说了。
知道大概的逻辑了现在进行一次简单unity逆向的复现。
还是下载文件并进行解压,然后可以看到这是个unity游戏,而且最开始看到这个我是打算用ce修改器做的,但是反复修改分数之后没用,我还以为跟分数无关。
先找到游戏的程序集文件。
可以看到程序集文件的路径如上,这里把程序集文件导入dnSpy进行反汇编查看其的源码。(相比之下我果然还是更喜欢dnSpy,因为这个界面感觉更帅点)
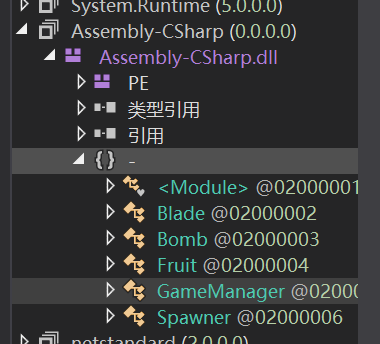
PE表示的是这个文件遵循和PE文件的格式,展开之后是这个文件的具体PE格式的成员
类型引用是说其它的文件里面定义的方法或者属性还是类型什么的被其所引用了哪些
引用则是说这个程序集引用了其它的程序集文件,从而使得这个程序集可以使用这个被引用的程序集里面的代码信息。
{}就表示一个被命名的空间或者是模块,这里代表的是这个被我们打开的文件的属于其本身的代码在这里面。
这里我们打开gamemanager这个模块(对名字理解之后的直觉说这个gamemanager可能藏得有东西,并且其它的地方如果藏东西其实很容易就被看到了,也许不需要打开这个文件,感觉上就是上面的都是前面的数据,而这个是后面的文件),我们打开gamemanager函数进行分析。最后找到如下关键的函数。
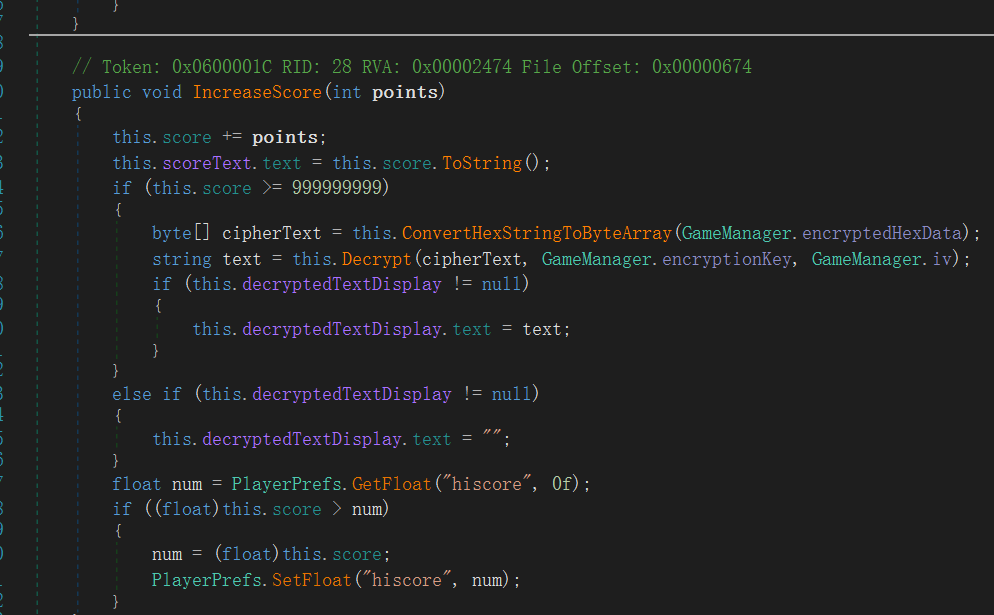
这里是增加分数的一个方法,可以看到其中一段代码是当分数达到999999999的时候,会输出一个字符串。这里我大概就猜到了,这个字符串就是flag,而且这个题目原本的目的应该是说就算不是预期解的dnSpy也可以做出来,那就是ce修改器修改分数后也可以拿到flag,但这里不知道为什么游戏有bug,导致flag弹不出来。
现在继续往下分析:
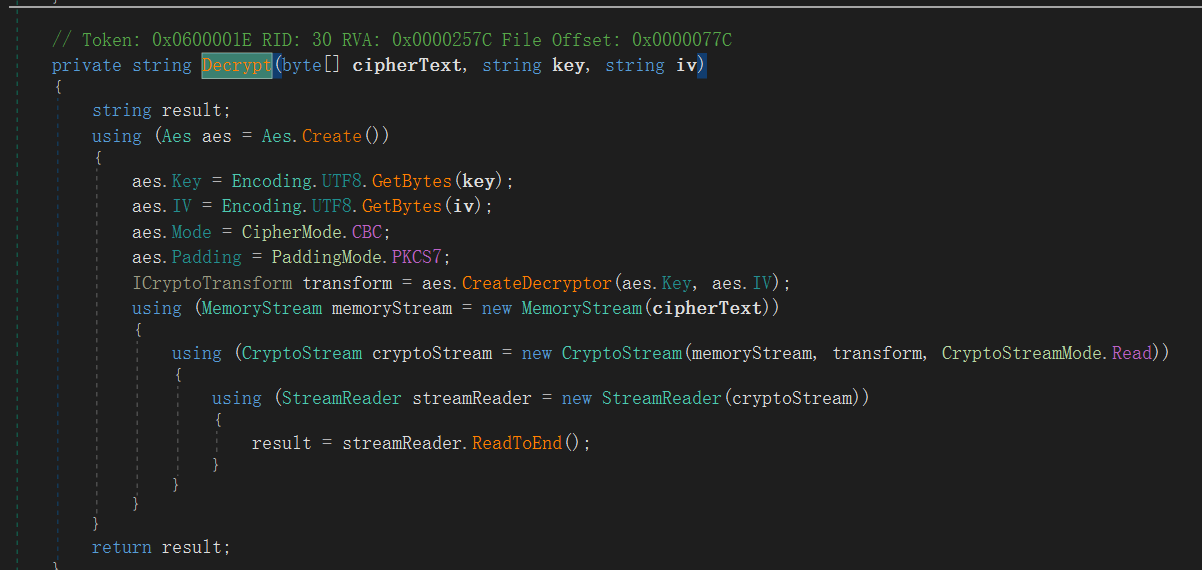
这里有个解密函数,我们根据名字可以知道这个是AES对称加密实现的。然后我们找到进行解密的数据。

密钥和加密字符串还有偏移量都给我们了,使用在线工具进行解密
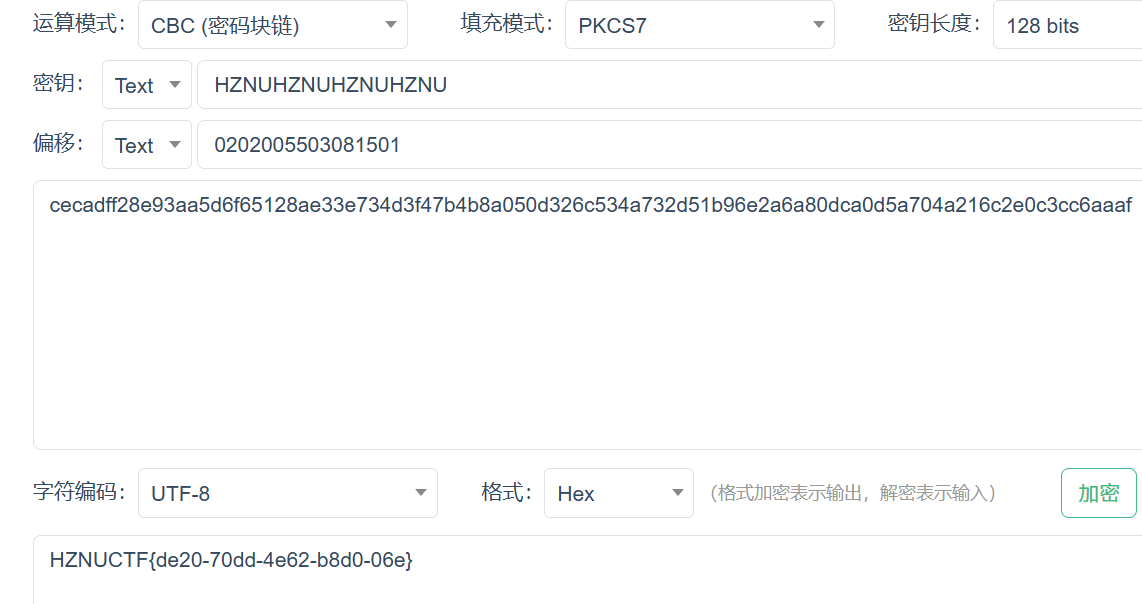
得到flag为:HZNUCTF{de20-70dd-4e62-b8d0-06e}
exchange(复现)
这个题目让我学到的是PE的文件头特征,先下载压缩包进行解压。
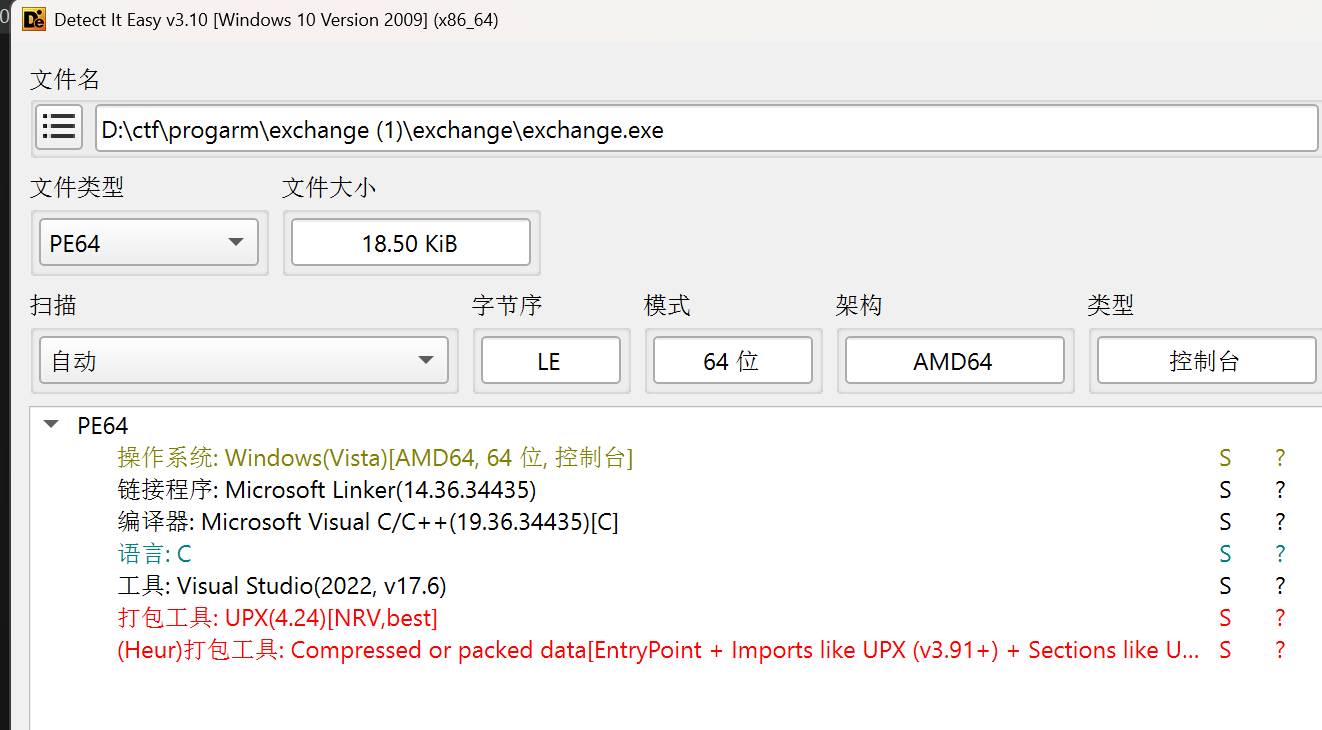
扫壳之后发现有upx壳,并且是64位的程序
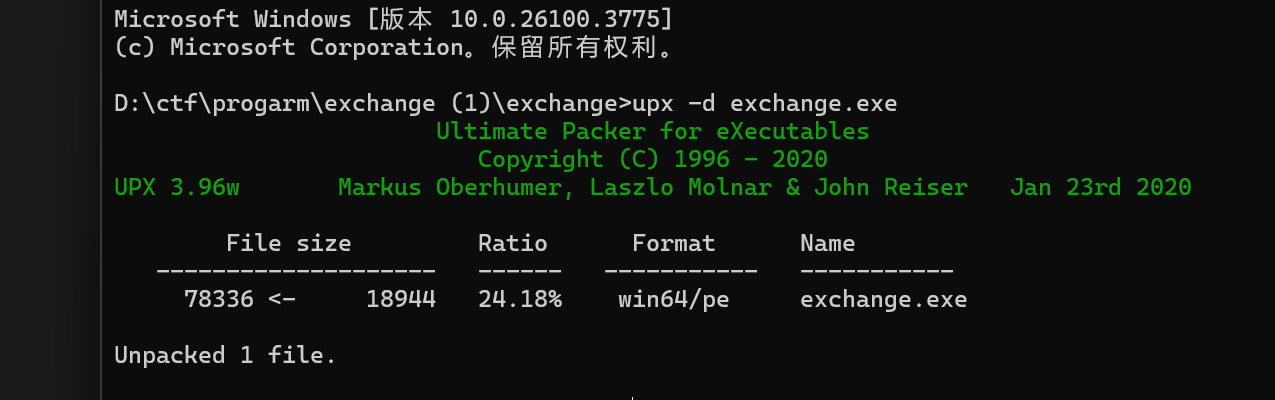
使用upx -d exchange.exe进行脱壳,脱壳成功后尝试运行,发现是无法正常运行的。
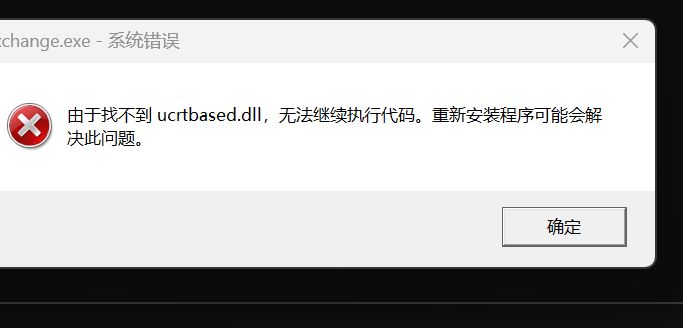
估摸着会用到010,用IDA64位进行打开。
发现其PE文件头的格式不对,并不是64位的文件头,而是32位的(0B 01),改成0B 02就好

然后继续进入IDA进行分析,先搜索出所有字符串,找到关键字符串之后然后索引到关键的函数。
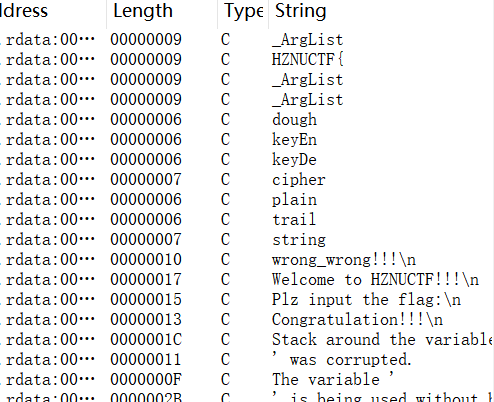
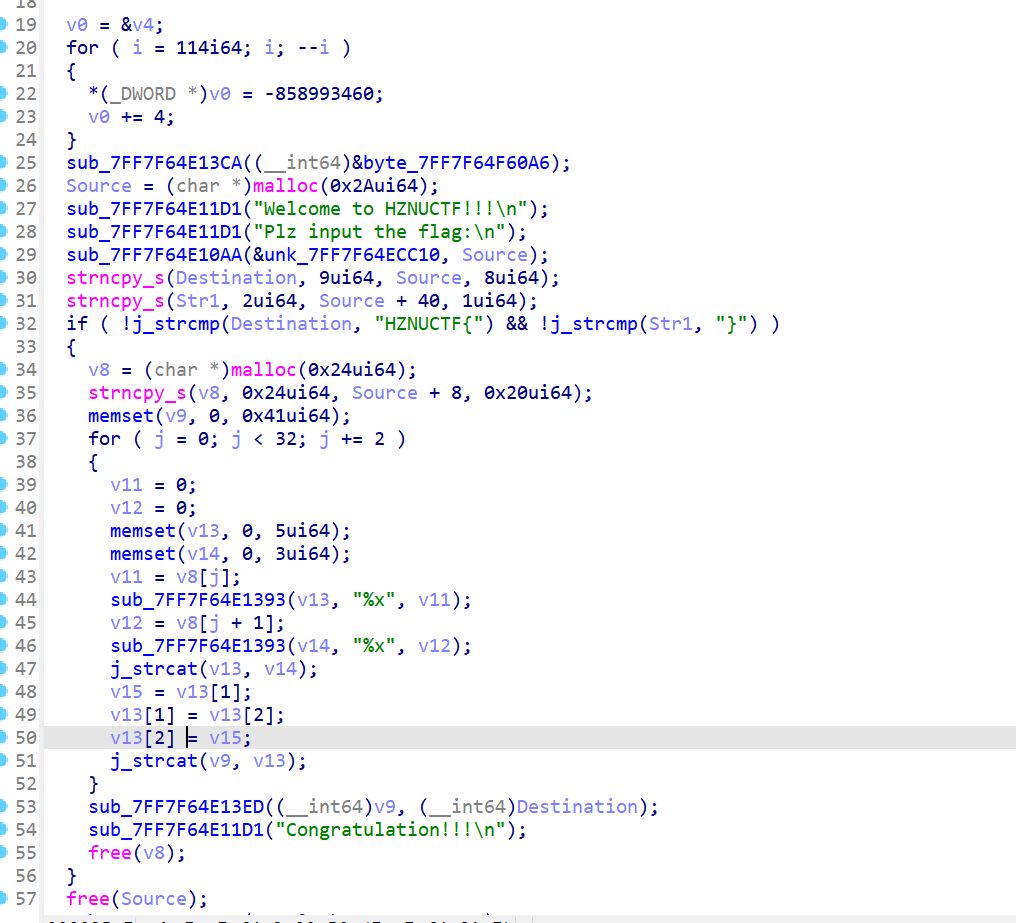
剩下的结合经验分析连蒙带猜进行分析也就可以得知函数的大概逻辑是如何,首先把字符的前缀HZNUCTF{复制给destination并进行验证,然后把字符串两个字符为一组分别处理成16进制并存在v13和v14中,把v14接在v13后面之后就把v13的中间两个字符进行交换然后进入到下面的函数进行加密。
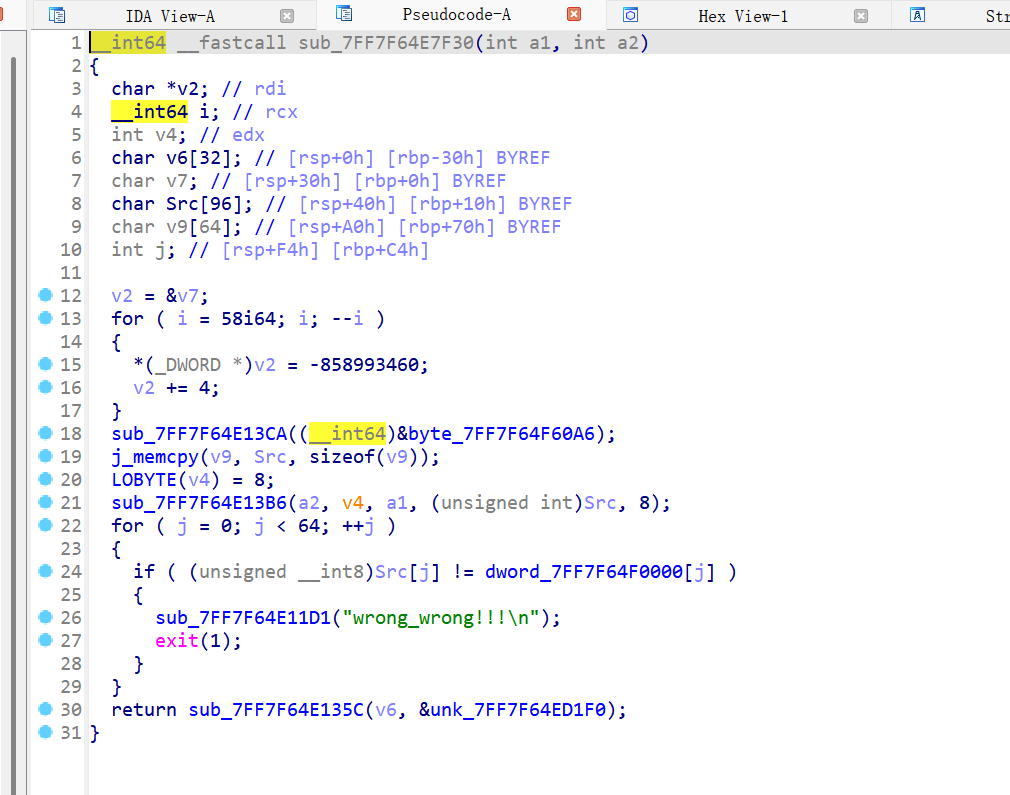
这个加密函数的作用使用findcrypto进行寻找就可以找到这个加密函数的作用。

这个是DES加密,这里我看官方WP之后发现这个DES是魔改的,虽然官方WP说只有totrot进行了修改,但是我看官方说这个标准的是1,2,4,6,8,10,12,14,15,17,19,21,23,25,27,28也不对,然后询问了ai看看。
虽然AI并不能全信,但其提供分析资料的能力还是很强的,官方说网上随便找个DES算法代码就可以进行解密了,但我尝试了好几次都没有成功,并且我看别人的解密代码并不像网上找到,要么就是修改伪代码的,要么就是找AI写的,也可能是自己对着伪代码写的,但总之这个不太可能是标准的DES算法并且只修改了totrot表,把sub_7FF7F64E13B6和dword_7FF7F64F0000的相关信息,以及这里面所有函数的相关信息给deepseek并开启深度思考模式最后可以得到解密代码,为了提高效率,这里我只要其得到其最后逆向解密得到的结果就可以。
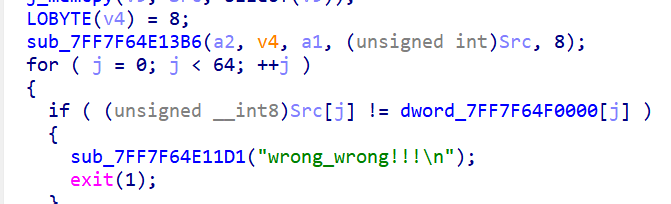
deepseek给我的数据是:333936147332632923d96353321d3345636826d26314621d3349330463126348
然后把这一串数据使用脚本作处理。
str0='333936147332632923d96353321d3345636826d26314621d3349330463126348'
for i in range(0,len(str0),4):
print(str0[i]+str0[i+2],end=' ')
print(str0[i+1]+str0[i+3],end=' ')
#33 39 31 64 73 32 62 39 2d 39 65 33 31 2d 34 35 66 38 2d 62 61 34 61 2d 34 39 30 34 61 32 64 38
然后使用cyberchef梭哈:
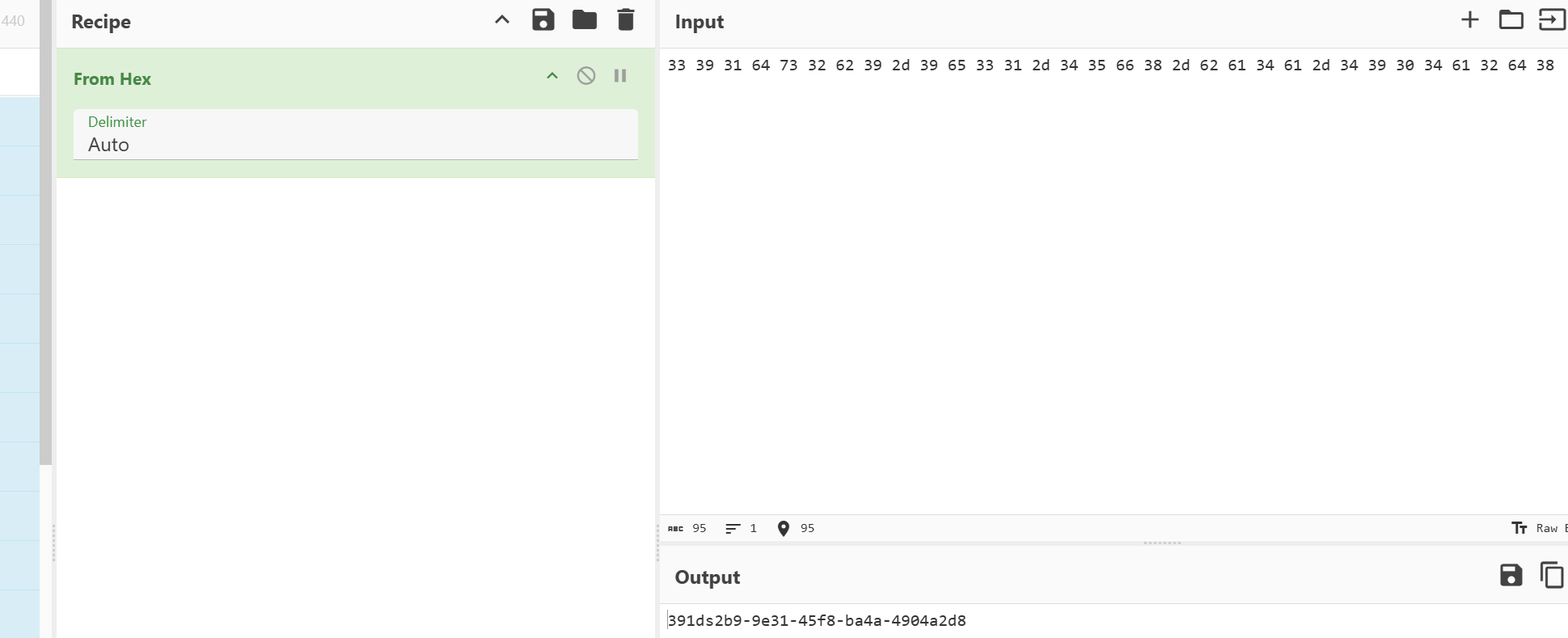
所以flag是HZNUCTF{391ds2b9-9e31-45f8-ba4a-4904a2d8}
这道题目最难的应该就是魔改后的DES算法的逆向了,因为这个DES不是魔改了一点,可能是官方写WP的时候不小心写错了吧。
剩下的re对我来说消化还是有点困难了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号