STL学习
栈和队列操作
使用标准库的栈和队列时,先包含相关的头文件
#include<stack>
#include<queue>
定义栈如下:
stack<int> stk;
定义队列如下:
queue<int> q;
栈:
s.empty() 如果栈为空返回true,否则返回false
s.size() 返回栈中元素的个数
s.pop() 删除栈顶元素但不返回其值
s.top() 返回栈顶的元素,但不删除该元素
s.push() 在栈顶压入新元素
队列:
q.empty() 如果队列为空返回true,否则返回false
q.size() 返回队列中元素的个数
q.pop() 删除队列首元素但不返回其值
q.front() 返回队首元素的值,但不删除该元素
q.push() 在队尾压入新元素
q.back() 返回队列尾元素的值,但不删除该元素
关于栈
栈是基本的数据结构之一,特点是先进后出,就如开进死胡同的车队,先进去的只能最后出来.
在c++ 中,stack的头文件是
#include<stack>
stack常用操作
stack<int> q; //以int型为例
int x;
q.push(x); //将x压入栈顶
q.top(); //返回栈顶的元素
q.pop(); //删除栈顶的元素
q.size(); //返回栈中元素的个数
q.empty(); //检查栈是否为空,若为空返回true,否则返回false
#include<iostream>
#include<stack>
using namespace std;
int main()
{
stack<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
q.push(5);
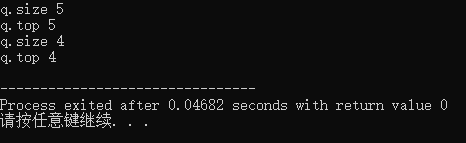
cout<<"q.size "<<q.size()<<endl;
cout<<"q.top "<<q.top()<<endl; //输出栈顶元素
q.pop(); //删除栈顶元素
cout<<"q.size "<<q.size()<<endl;
cout<<"q.top "<<q.top()<<endl;
return 0;
}
关于队列
队列(queue)与栈一样,是一种线性存储结构,它具有如下特点:
(1)队列中的数据元素遵循“先进先出”。
(2)在队尾添加元素,在队头删除元素。
2、队列的相关概念:
(1)队头与队尾: 允许元素插入的一端称为队尾,允许元素删除的一端称为队头;
(2)入队:队列的插入操作;
(3)出队:队列的删除操作。
a、栈空: 队首标志=队尾标志时,表示栈空。
b、栈满 : 队尾+1 = 队首时,表示栈满。
用数组模拟实现队列
用STL中自带的queue(常数比priority_queue大很多,慎用)?
① 数组模拟队列
以数组作为底层数据结构时,一般讲队列实现为循环队列。这是因为队列在顺序存储上的不足:每次从数组头部删除元素(出队)后,需要将头部以后的所有元素往前移动一个位置,这是一个时间复杂度为O(n)的操作。
循环队列,可以把数组看出一个首尾相连的圆环,删除元素时将队首标志往后移动,添加元素时若数组尾部已经没有空间,则考虑数组头部的空间是否空闲,如果是,则在数组头部进行插入。参考博客:,判断循环队列是“空”还是“ 满”,有两种处理方法:
A. 设置状态标志位以区别空还是满
B. 少用一个元素,约定“队头front在队尾rear的下一个位置(指的是环的下一个位置)”作为“满”的标志
定义front为队列头元素的位置,rear为队列尾元素的位置,MAXSIZE为循环队列的最大长度。
A. 求元素的个数:(rear - front + MAXSIZE) % MAXSIZE
B. front/rear指向逻辑的下一个空间 front =(front+1)%MAXSIZE,rear = (rear+1)%MAXSIZE
C. 判空:front == rear
D. 判满:(rear+1+MAXSZIE) == front
定义 int que[100],L = 1,R =0;
队列不空 while(L<=R)
新元素入队 que[++R] = i;
取队首元素并出队
int cur = que[L++];
②自带STL queue
定义 queue<int> q;
队列不空 while(!q.empty())
新元素入队 q.push(m);
取队首元素 q.front();
队首元素出队 q.pop();
③结构体队列
可以看出用法还是差不多的,只是将整形换成自己定义的结构体一样。
就是把int换成结构体!
④优先队列
定义:就是用个东西把一群元素排队(默认从大到小,可更改为从小到大)
库: #include<queue>
定义队列:
priority_queue<int(或其他类型)> q
priority_queue<int,vector<int>,greater<int>> q(队列从小到大排序)
//基本操作: (其中q为定义的队列)注意它没有队列的q.back()
q.push(x)// x为定义的变量,将x压进队列
q.top() // 返回队列第一个元素
q.pop() // 删除队列第一个元素
q.size() // 返回队内元素数量
q.empty() // 判断队列是否空,空则返回1,否则返回0;
例子1、简单的队列操作:
#include <queue>
#include <iostream>
using namespace std;
int main(){
queue<int> q;
for (int i = 0; i < 10; i++){
q.push(i);
}
if (!q.empty()){
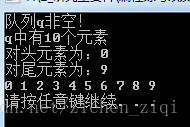
cout << "队列q非空!" << endl;
cout << "q中有" << q.size() << "个元素" << endl;
}
cout << "队头元素为:" << q.front() << endl;
cout << "队尾元素为:" << q.back() << endl;
for (int j = 0; j < 10; j++){
int tmp = q.front();
cout << tmp << " ";
q.pop();
}
cout << endl;
if (!q.empty()){
cout << "队列非空!" << endl;
}
system("pause");
return 0;
}
关于set
set就是集合,STL的set用二叉树实现,集合中的每个元素只出现一次(参照数学中集合的互斥性),并且是排好序的(默认按键值升序排列)
访问元素的时间复杂度是 O(log2n)
set具有迭代器set
set<int> q; //以int型为例 默认按键值升序
set<int,greater<int>> p; //降序排列
int x;
q.insert(x); //将x插入q中
q.erase(x); //删除q中的x元素,返回0或1,0表示set中不存在x
q.clear(); //清空q
q.empty(); //判断q是否为空,若是返回1,否则返回0
q.size(); //返回q中元素的个数
q.find(x); //在q中查找x,返回x的迭代器,若x不存在,则返回指向q尾部的迭代器即 q.end()
q.lower_bound(x); //返回一个迭代器,指向第一个键值不小于x的元素
q.upper_bound(x); //返回一个迭代器,指向第一个键值大于x的元素
q.rend(); //返回第一个元素的的前一个元素迭代器
q.begin(); //返回指向q中第一个元素的迭代器
q.end(); //返回指向q最后一个元素下一个位置的迭代器
q.rbegin(); //返回最后一个元素
set单元素应用
#include<iostream>
#include<set>
using namespace std;
int main()
{
set<int> q; //默认按升序排列
q.insert(5);
q.insert(5);
q.insert(5);
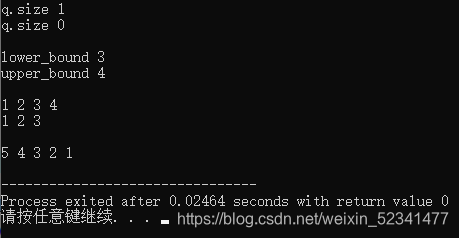
cout<<"q.size "<<q.size()<<endl; //输出 1 ,在set插入中相同元素只会存在一个
q.clear(); //清空set
cout<<"q.size "<<q.size()<<"\n\n";
q.insert(4);
q.insert(4);
q.insert(3);
q.insert(3);
q.insert(2);
q.insert(1);
cout<<"lower_bound "<<*q.lower_bound(3)<<endl; //返回3
cout<<"upper_bound "<<*q.upper_bound(3)<<"\n\n"; //返回4
set<int>::iterator i;
for( i=q.begin();i!=q.end();i++) //set的遍历
cout<<*i<<" "; //输出1 2 3 4,可见自动按键值排序
cout<<endl;
q.erase(4); //删除q中的 4
for(i=q.begin();i!=q.end();i++) //再次遍历set 只输出 1 2 3
cout<<*i<<" ";
cout<<"\n\n";
set<int,greater<int>> p; //降序排列
p.insert(1);
p.insert(2);
p.insert(3);
p.insert(4);
p.insert(5);
for(i=p.begin();i!=p.end();i++)
cout<<*i<<" ";
cout<<endl;
return 0;
}
set多元素应用(结构体)
#include<iostream>
#include<set>
using namespace std;
struct node{
int a,b;
bool operator< (const node W)const
{
return a>W.a; //按a的值升序
}
}t;
int main()
{
set<node> q;
t.a=1;
t.b=2;
q.insert(t);
t.a=4;
t.b=2;
q.insert(t);
t.a=3;
t.b=5;
q.insert(t);
set<node>::iterator i;
for(i=q.begin();i!=q.end();i++)
{
t=*i;
cout<<t.a<<" "<<t.b<<endl;
}
return 0;
}
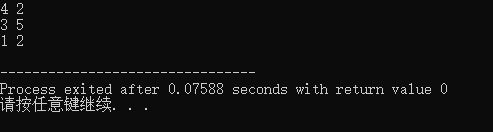
这段代码定义了一个结构体node,在结构体内部重载了小于操作符<,使得结构体node可以被用于set这种基于红黑树的数据结构中。
在重载的<操作符中,定义了如果当前节点的a大于另一个节点W的a,则认为当前节点小于另一个节点。这样就可以使得set按照a的值从大到小进行排序。
在主函数中,先创建了一个set
set.count()用法
set::count()是C++ STL中的内置函数,它返回元素在集合中出现的次数。由于set容器仅包含唯一元素,因此只能返回1或0。
用法:set_name.count(element)
参数:该函数接受一个强制性参数element,该元素指定要返回其计数的元素。
返回值:该函数返回1或0,因为该集合仅包含唯一元素。如果设置的容器中存在该值,则返回1。如果容器中不存在它,则返回0。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int arr[] = { 14, 12, 15, 11, 10 };
// initializes the set from an array
set<int> s(arr, arr + 5);
// check if 11 is present or not
if (s.count(11))
cout << "11 is present in the set\n";
else
cout << "11 is not present in the set\n";
// checks if 18 is present or not
if (s.count(18))
cout << "18 is present in the set\n";
else
cout << "18 is not present in the set\n";
return 0;
}
输出:
11 is present in the set
18 is not present in the set



 浙公网安备 33010602011771号
浙公网安备 33010602011771号