语言模型和 RNN 笔记 (CS224N-4)
语言模型定义
(1)语言模型任务是根据给定的单词序列计算下一个单词的概率分布,完成这样的任务的系统就被称作语言模型
(2)也可以认为语言模型是一个为文本分配概率的系统,例如文本 \(x^{(1)},\cdots,x^{(T)}\) 的概率是

n-gram语言模型
(1)一个n-gram是由n个连续单词组成的一块文本,收集不同n-gram的频率统计数据,并使用这些数据预测下一个单词
(2)思路
①首先我们做一个Markov假设, \(x^{(t+1)}\) 仅取决于其前面的n-1个单词

②如何得到这些n-gram和(n-1)-gram的概率:
在大型文本语料库计算它们,统计概率近似
(3)存在的问题:
-
稀疏性问题:当我们需要的预测条件文本根本没有出现在语料库中,解决方法如下
①添加小的\(\sigma\)扰动因子给每一个语料库中的单词(smoothing)
②以需要文本的前一部分作为预测条件(backoff) -
存储问题:需要存储语料库中所有n-gram的数量,增加n或增加语料库都会增加模型大小
-
当生成长文本时,文本虽然语法连贯但会变得牛头不对马嘴
基于固定窗口的神经网络语言模型
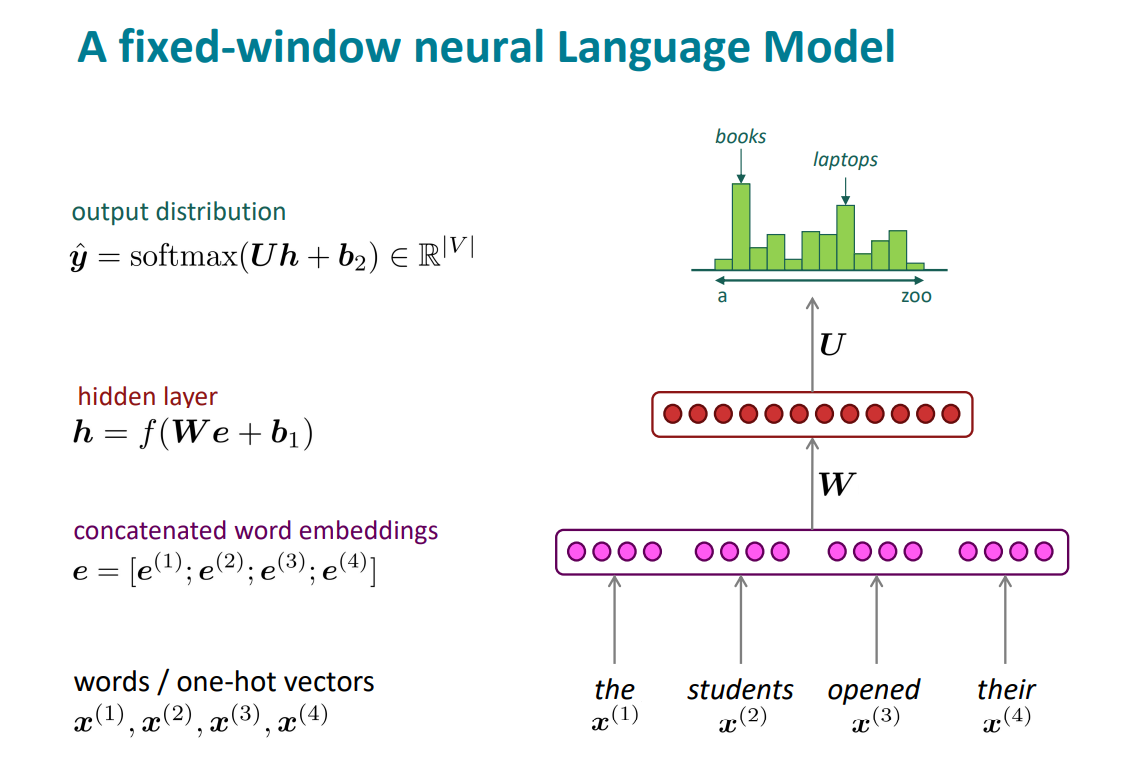
①改进:没有稀疏性问题,不需要存储所有的n-gram
②问题:窗口太小,需要放大,但是放大窗口也会放大模型
RNN
(1)RNN全称:Recurrent Neural NetWorks(递归神经网络)
(2)核心思路:反复的应用相同的权重
(3)优缺点:
①优点:可以处理任何长度的输入,对于较长的输入上下文,模型大小不会增加
②缺点:递归计算很慢,很难从许多步骤后访问信息
(4)前向传播:

①获取一个大的文本语料库,它是一个单词序列
②将单词序列输入RNN模型,计算每一个步骤t的输出分布,上一步的输出是下一步的输入
③步骤t上的损失函数是预测的概率分布 \(\widehat y^{(t)}\) 和真正的下一个单词的概率分布 \(y^{(t)}\) ( \(x^{(t+1)}\) 的one-hot编码)之间的交叉熵
④将其平均化,已获得整个训练集的整体损失
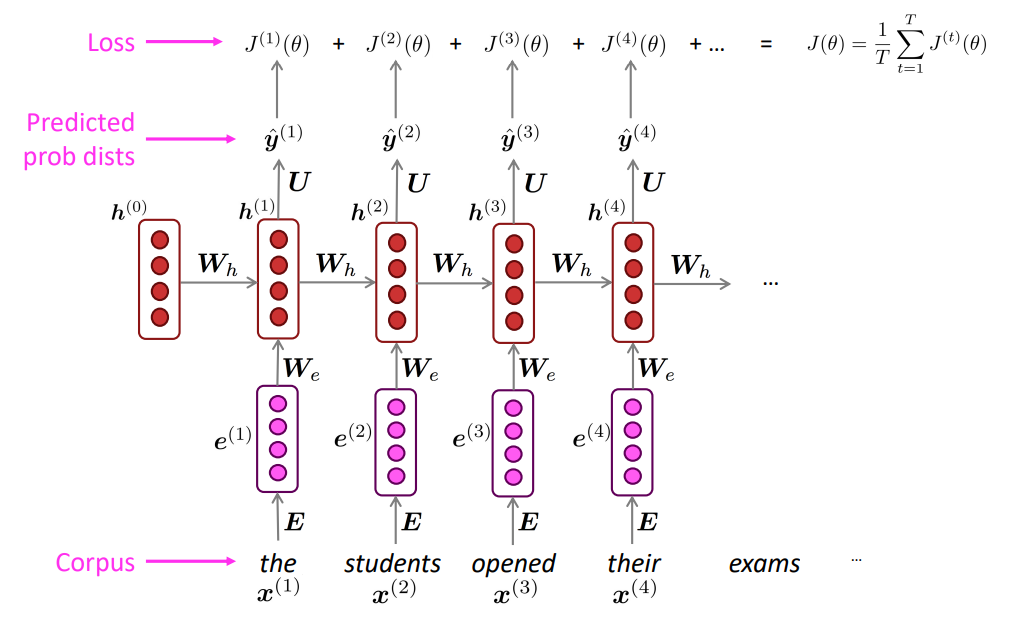
然而,一次计算整个语料库的损失梯度和代价太昂贵了,在实践中,我们将 \(x^{(1)},\cdots,x^{(T)}\) 作为句子或文章。计算一个句子(实际上是一批句子)的损失,计算梯度并更新权重,对新一批句子重复。
(5)反向传播
多变量链式法则:

(6)RNN中的梯度消失和梯度爆炸:
-
梯度消失:如果权重很小,由推导得梯度为权重的距离数指数,所以距离一长就会导致无法预测类似的长距离依赖关系(即无法在长距离保存信息)

-
梯度爆炸:同理,如果权重很大会导致梯度很大,进而会导致糟糕的更新,梯度下降时会走很大的一步
解决方案:梯度裁剪,当梯度大于某一个阈值,就在应用SGD更新之前缩小它
语言模型的评估
(1)困惑度(perplexity)
(这其实就等于交叉熵损失的指数)

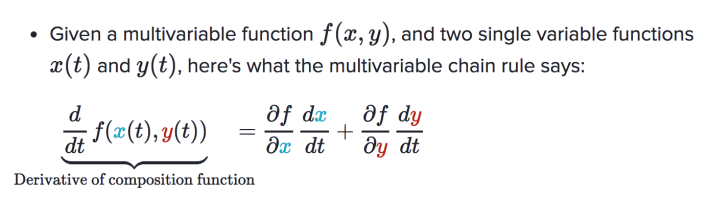

 浙公网安备 33010602011771号
浙公网安备 33010602011771号