激活函数汇总

激活函数

激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。

Sigmoid

(1) 公式：\(S(x)=\frac{1}{1+e^{-x}}\)

(2) 函数图：

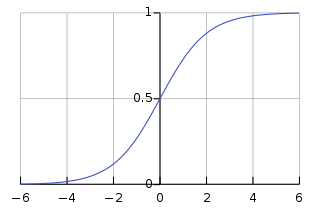
(3) 缺点：
① 输出值落在(0,1)之间，期望均值为0.5，不符合均值为0的理想状态
② 该函数存在一正一负两块“死区”（死区：梯度计算为0，靠近死区的部分梯度也会非常小）

Softmax

(1) 公式：\(S_i=\frac{e^{x_i}}{\sum_je^{x_j}}\)

Tanh

(1) 公式：\(\tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}\)

(2) 函数图：

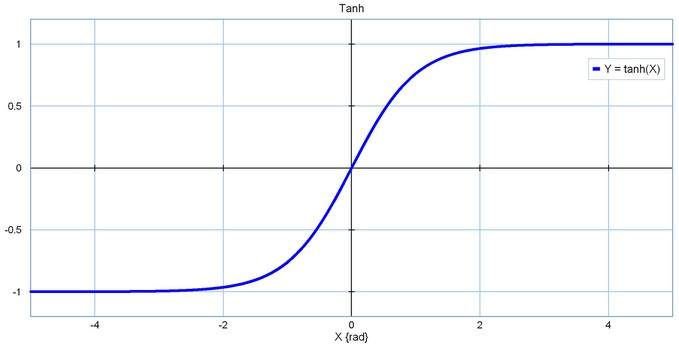
(3) 优点：将期望均值平移到0这一理想状态

(4) 缺点：本质上仍是sigmoid函数，无法回避一左一右两块死区

ReLU

(1) 公式：\(f(x)=\max (0,x)\)

(2) 函数图：

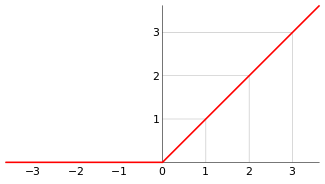
(3) 优点：
① 彻底消灭了正半轴上的死区，可以解决梯度消失问题
② 计算超简单
③ 有助于模型参数稀疏

(4) 缺点：
① 期望均值跑得离0更远了
② 负半轴上的死区直接蚕食到了0点（存在“神经元死亡”问题，如果激活函数的输入都是负数，那么该神经元再也无法学习）

单侧饱和：
Simoid函数是双侧饱和的，意思是朝着正负两个方向，函数值都会饱和；但ReLU函数是单侧饱和的，意思是只有朝着负方向，函数值才会饱和。

理解单侧饱和的意义：将神经元比作检测某种特定特征的开关。当开关处于开启状态，说明在输入范围内检测到了对应的特征。正值越大代表检测到特征越明显，而负值越小则代表没有检测到特征越明显，但没有检测到特征就是没有检测到，本身不具有程度，所以这些负值的大小属于噪声信息。

所以ReLU将负值截断成0不仅为网络引入了稀疏性，还使得神经元对于噪声干扰更具鲁棒性。

Leaky ReLU

(1) 函数图：

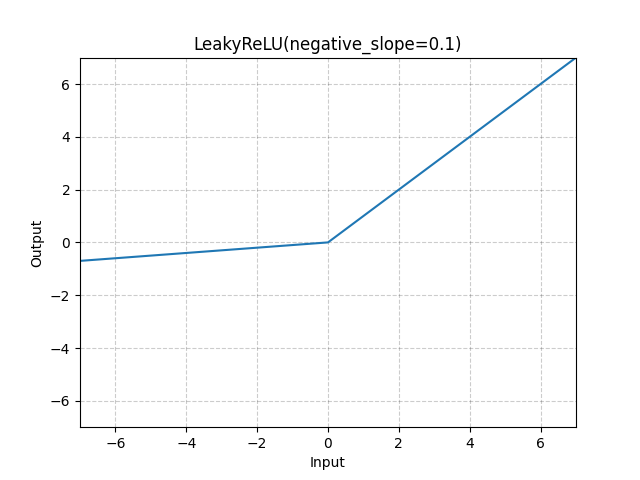
(2) 优点：消除了负半轴上的死区，解决了“神经元死亡”问题

(3) 缺点：
① 期望均值依然不为0
② 合适的\(\lambda\)值较难设定且敏感，导致在实际使用中性能不稳定

PReLU

(1) \(\lambda\)参数是学习得到的

Elu

(1) 函数图：

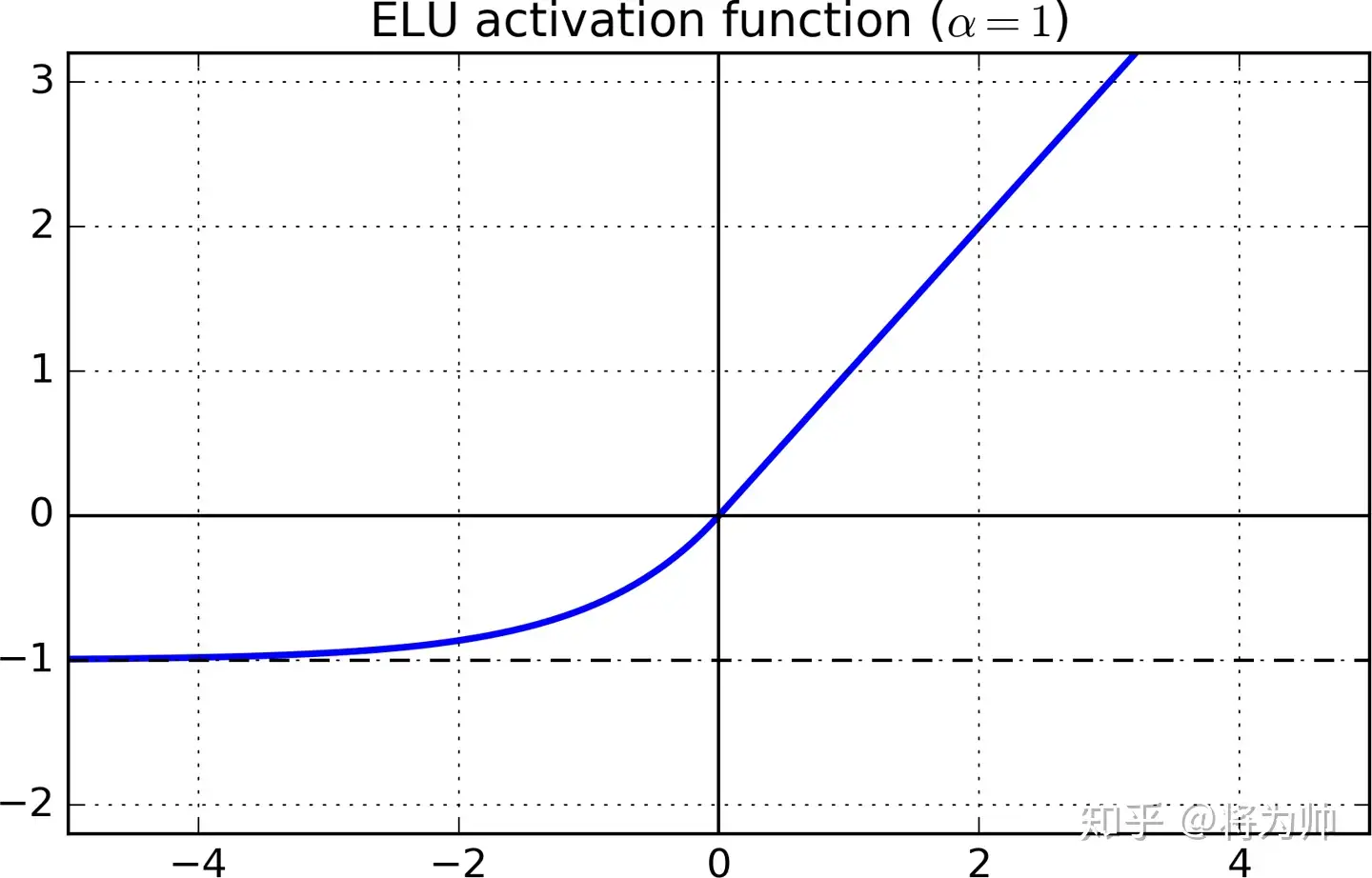
(2) 优点：完美解决死区问题，具有单侧饱和

(3) 缺点：均值仍不是0

选择合适的激活函数

一般优先选用 ReLU，效果不好的话可以再尝试使用 LeakyReLU 或 ELU。如果计算资源不成问题，且网络并不十分巨大，可以试试 ELU，否则，最好选用 LeakyReLU