凋叶棕

T1

大众分：\(100\text{pts}\)。

\(p->S->f_S->|S|!|V-S|!\)。

\(O(2^n(n+m))\)。

\(O(2^n n)\)。

T2

大众分：\(60\text{pts}\)。

小花🐱。

小🐱排除集合信息。小🐱宣布胜利。\(vic_S \neq vic_T\) 爆。小🐱宣布胜利。小🐱四种情况。爆。

T3

大众分：\(70\text{pts}\)。

小🐱。要拍照。子序列不是子串。不能为空。白🐱=黑🐱。对。为什么不打暴力。🐱🐱。

括号匹配。()。

咕咕嘎嘎。

好题啊，比 CF Div.1 和 AGC 质量高多了。

---

T1

做复杂了，写了一个神秘的维护增量做法。但是思维含量极低。也许是做简单了？（对我来说。）

正解做法是枚举一棵树，然后枚举它有贡献的状态。一旦每次枚举都有效，时间复杂度显然就是 \(O(2^n n)\) 的。

T2

好题啊。设 \(dp_{i,S}\) 表示，卡片集合为 \(S\) 时，第 \(i\) 轮才第一次宣布胜利的猫猫集合是什么。设 \(C\) 代表真正的卡片集合，那么扫一遍 \(dp_{i,C}\) 就能求出答案。

\(dp_{i,C}\) 怎么求呢？一个猫猫会在第 \(i\) 轮宣布胜利，当且仅当对于它来说合法的状态只对应一种答案。于是，还需要一个 \(f_{i,S}\)，代表第 \(i\) 轮只通过公开信息（不包括看到的卡牌信息）判断，\(S\) 是否合法。

于是 check 一个猫猫是否会在第 \(i\) 轮宣布胜利，只用看对于它来说的 \(4\) 种可能状态对应的值就行了。

\(f_{i,S}\) 怎么转移呢？首先，如果和信息冲突，就直接将其设为 false，这是显然的。但还有一种转移是，如果 \(dp_{i,S}\) 不等于实际情况，它也是 false。

具体流程如下：

• 根据公布的信息更新 \(f_{i,S}\)。
• 用 \(f_{i,S}\) 更新 \(dp_{i,S}\)。得到实际上有哪些猫猫在第 \(i\) 轮宣布胜利。设这个猫猫集合为 \(T\)。
• 再次用 \(T\) 更新 \(f_{i,S}\)。这很显然是对的，不会存在 \(f\) 和 \(dp\) 互相转移的情况。当然，这里的 \(f_{i}\) 要继承到 \(f_{i+1}\) 去。

时间复杂度 \(O(2^nmn+2^n\sum p)\)。

为啥一定要设 \(2^n\) 的状态呢，明明每只猫猫可能的状态只有 \(4\) 种啊。

更新 \(dp_{i,S}\) 的时候会 check 一只猫猫是否合法，会去看 \(f\) 的 \(4\) 个状态。然而，用 \(T\) 更新 \(f\) 的时候，必须要知道其 \(dp\) 值。也就是说，它会一直扩展下去，转移不止和 \(4\) 个状态有关。

反正非常酷炫。刚刚想了一下感觉很有道理。像一条猜疑链。

T3

JOI 的题质量貌似都很高。一个比较显然的观察：第 \(i\) 个 W 只会和第 \(i\) 个 B 匹配。

哈哈哈，仔细想想发现这个观察其实并不显然。不过既然它是一个匹配关系，而且能被划分的条件是把 W 看成 \(1\)，B 看成 \(-1\) 时前缀和都 \(\geq 0\)，那么可以把它转化成网格图。

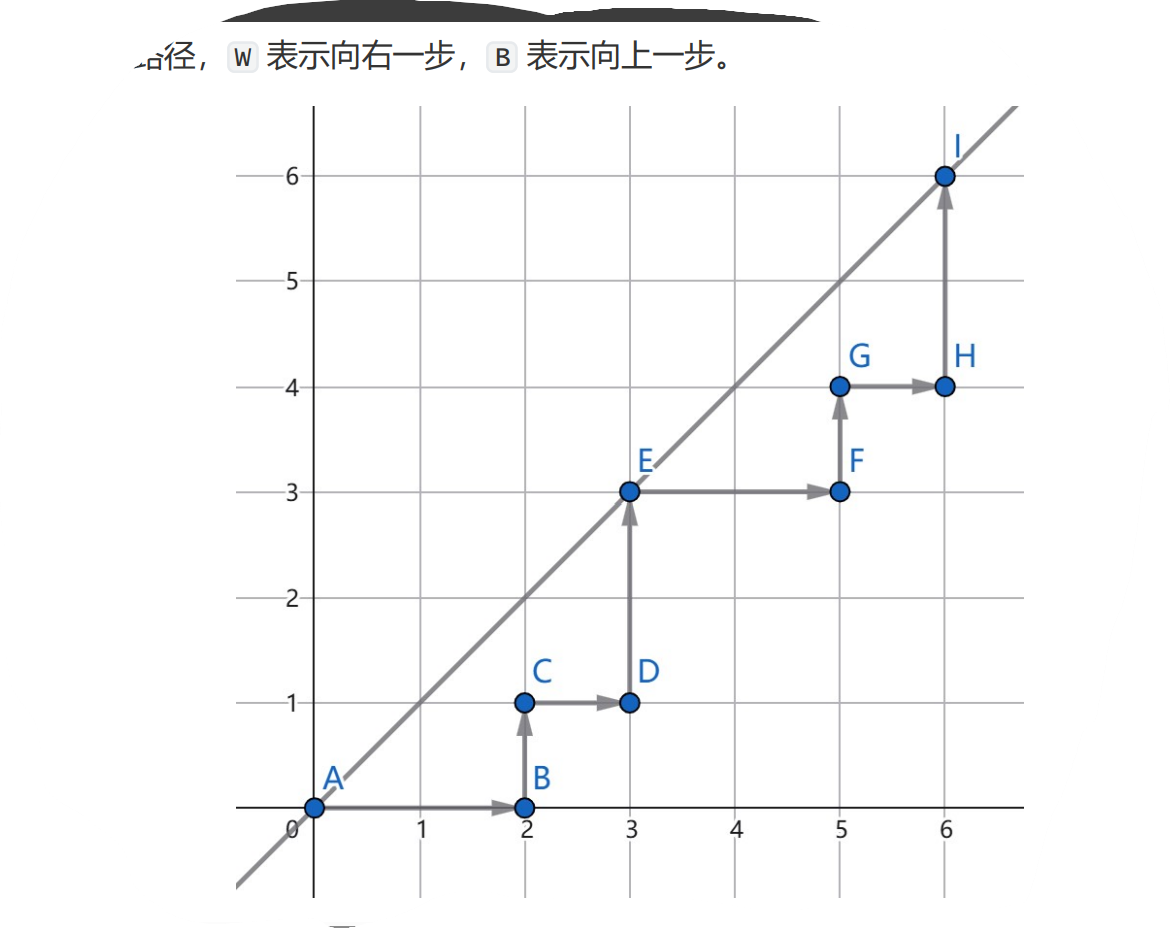
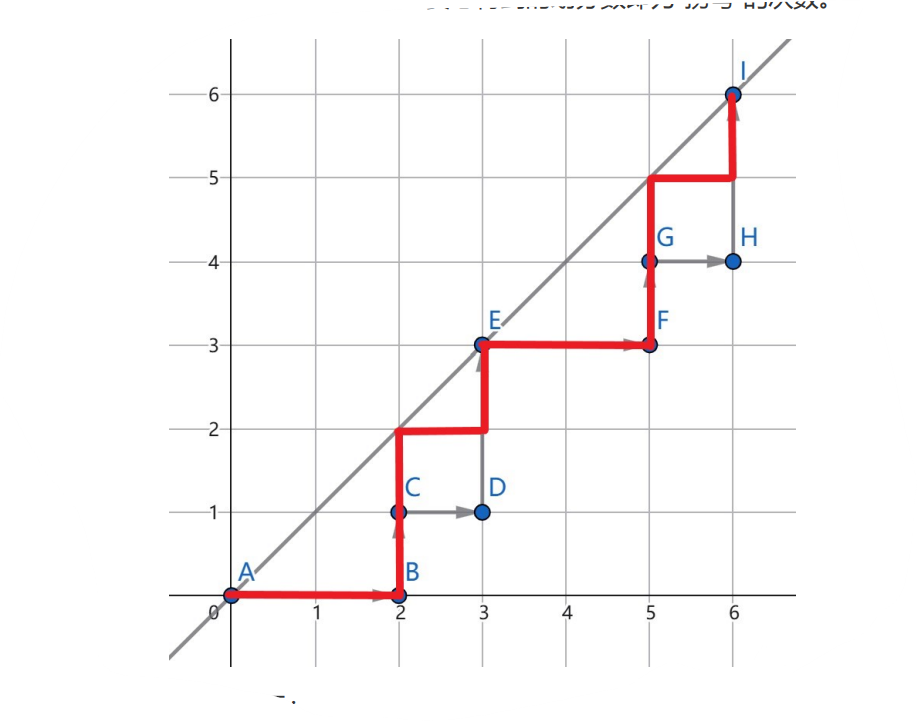
直接贪心地匹配，大概就是这样的。有多少个直角三角形就是拍了多少张照片。这样来看，上述观察就非常显然了。而且有个更加重要的性质：一张照片只会包含编号在 \([l,r]\) 中的 W 和编号在 \([l,r]\) 中的 B，即使它们在原序列上可能不连续。

这个性质是非常非常非常方便我们 DP 的！设 \(dp_{i,j}\) 表示，考虑到前 \(i\) 个 W 和前 \(i\) 个 B 时，共拍了 \(j\) 张照片的最小操作次数。

显然有转移 \(dp_{i,j}=\min\limits_{k=1}^i w(k,i)+dp_{k-1,j-1}\)，其中 \(w(l,r)\) 就是让编号在 \([l,r]\) 中的 W 移到对应的 B 前面所需的最小操作次数。

先考虑当前有解的话，\(w(l,r)\) 怎么算。假设第 \(l\) 个 W 到第 \(r\) 个 W 中间存在第 \(x\) 个 B 满足 \(x<l\)，那么它其实是不重要的，因为没有人需要跨过它。如果存在第 \(x\) 个 B 满足 \(x>r\)，那么这是无解的，不用考虑。因此，会带来代价的 B 只有 \([l,r]\) 中的 B。于是 \(w(l,r)=\sum\limits_{i=l}^r \max(c_i-(l-1),0)\)，其中 \(c_i\) 代表第 \(i\) 个 W 前有几个 B。这个式子是显然的，因为想要保证这个条件，就必须满足 \([l,r]\) 中的每个 W 前面最多有 \(l-1\) 个 B。

然后发现我神秘了。无解的话也能这样算，然后就能变成有解。That's good。

发现 \(w(l,r)\) 是凸的，于是直接 wqs 二分。哈哈哈。

发现可以斜率优化，于是做到 \(O(n\log n)\)。哈哈哈。