CF 1053 Div.2

E. Limited Edition Shop

经过一些简单转化，要解决的是如下问题：

二维平面上有 \(n\) 个点，点有点权。\(n\) 个点横坐标、纵坐标都是 \(1\sim n\) 的排列。要求选择若干点，满足它们右下角区域的并集中的点点权和最大。

考虑 \(dp\)。设 \(dp_i\) 表示考虑到从左往右第 \(i\) 个点时（必选）答案的最大值。

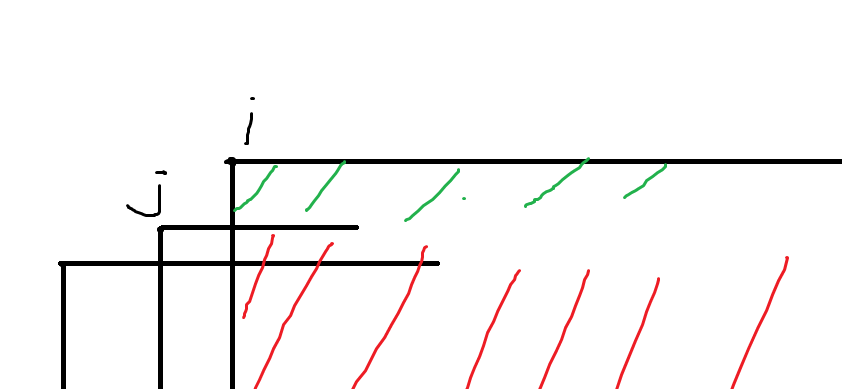
如图所示，如果 \(i\) 想从 \(j\) 转移，需要加上绿色部分的点权和。这可以转化成绿色+红色部分的点权和减去红色部分的点权和。其中，绿色部分的点权和可以直接算，红色部分的点权和可以在 \(j\) 处处理。当 \(i\) 增加时，红色部分去掉一列。这一列只可能有一个点 \((i,y_i)\)。所以对于所有 \(j<i\) 且 \(y_j>y_i\)，红色部分都会减去该点权。这启示我们使用线段树维护，时间复杂度 \(O(n\log n)\)。线段树下标是 \(y_i\)，原因显然。

F. Attraction Theory

观察原始 \(p\) 序列显然是没有用的，我们改为观察 \(p\) 的桶数组 \(f\)。经过思考，发现如下事实：

• \(f\) 中有值的位置一定连续。
• 设这段连续的位置为 \([L,R]\)，那么需要满足对于所有 \(L<i<R\)，\(f_i\) 是奇数。
  这两个条件都可以归纳证明。并且可以发现，这两个条件是充要的，任意一个满足条件的 \(f\) 都可以简单构造出一种合法的方案。

现在这个题就是一个纯粹的计数题了。假设 \(L=1\)，我们枚举区间长度 \(Len\)。因为 \(f\) 要满足奇偶性限制，我们不妨将 \(f\) 数组处理一下得到 \(g\) 数组。具体地，

• \(f_1 = 2g_1 + x(1 \leq x \leq 2)\)
• \(f_{Len} = 2g_{Len} + y(1\leq y \leq 2)\)
• \(f_i = 2g_i + 1(1<i<Len)\)

因为 \(f_i\geq 1\)，所以显然，\(g_i \geq 0\)。

设 \(S=n-x-y-(Len-2)\)，则显然 \(\sum g_i = \frac{S}{2}\)，因为 \(\sum f_i = n\)。所以我们要求所有的 \(\sum 2g_ia_i\)。还有一些 \(x,y,1\) 之类的常数可以稍后处理。然后发现，\(g_i\) 是相当线性的，并且只考虑 \(g\) 的和的话，各个 \(g_i\) 之间并没有什么区分，也就是说它们是对称的。因此，我们可以发现，所有方案中每个 \(g_i\) 的和是分别相同的！

也就是说，\(g_i\) 的期望值是 \(\frac{S}{2Len}\)。所以 \(\sum 2g_ia_i\) 就等于 \(cnt\sum 2\times\frac{S}{2Len}a_i\)，其中 \(cnt\) 是 \(g\) 的方案数。然后就非常简单的做完了。\(L \neq 1\) 的情况是类似的，可能要再推一下式子吧。常数处理是简单的，时间复杂度好像可以做到 \(O(n)\)。

为什么 \(1\leq x,y\leq 2\) 呢？如果 \(0\leq x,y\leq 1\)，那么 \(x=0\) 时 \(g_1\) 就不能等于 \(0\) 了！这样是很烦的。不过若 \(1\leq x,y\leq 2\)，那么就只需要满足 \(g_1\geq 0\) 了。非常好。

G1. Hidden Single (Version 1)

\(4n+\lceil 2\log_2 n\rceil\) 的询问次数一看就非常分治。

设 Solve(int l,int r,vector waste,vector val) 是我们的分治函数，其中，

• 当前能确定答案在 \([l,r]\) 中。
• \(val\) 中的元素全部出现在 \([l,r]\) 中。
• \(waste\) 中的元素既有出现在 \([l,r]\) 里的，又有出现在 \([l,r]\) 外的。

对于出现在 \(val\) 中的元素：

询问两次，分别看 \([l,mid]\) 与 \([mid+1,r]\) 中有没有该元素。如果都有，加入下一个区间的 \(waste\)。

对于出现在 \(waste\) 中的元素：

询问一次，看 \([l,mid]\) 中有没有该元素。通过这个，我们能知道 \([mid+1,r]\) 中有没有该元素。

如果当前区间长度为 \(Len\)，询问次数最多为 \(Len+1\)。因为出现次数为 \(2\) 的 \(val\) 中元素会询问两次。\(waste\) 中元素只会在当前区间中出现一次。基本上就是区间中每个数出现多少次就会被询问多少次，除了出现次数为 \(1\) 的 \(val\) 中元素，即答案。所以询问次数最多为 \(Len+1\)，这很显然。

然后能证明区间长度的和加区间个数是小于等于 \(4n+\lceil 2\log_2 n\rceil\) 的，于是这道题就做完了。

G2. Hidden Single (Version 2)

我们考虑另外一种做法。

设 Solve(vector<int>V,vector<int>S) 是我们的递归函数，其中，

• \(V\) 是当前的下标集合。
• \(S\) 是当前的候选值集合。

每次做这样一件事情：

将下标集合划分为 \(V1,V2\) 两个大小相等的集合，对于出现在 \(S\) 中的元素：

询问两次，看是否 \(V1,V2\) 中都有该元素。如果是，这个元素就没有用了，直接丢掉。否则，放进它存在那边的候选值集合。然后往两边递归。

如果某个下标集合和其对应的候选值集合大小都为 \(1\)，那么我们就找到了答案。

这个做法看起来非常没有道理。不过我们仔细分析可以发现，每个元素的期望查询次数为 \(4\) 次！因为不出现在同一边的概率为 \(\frac{1}{2}\)，所以一个元素在期望 \(2\) 次递归过后就不会出现在同一边。每次递归查询 \(2\) 次，单个元素的期望查询次数就是 \(4\) 次。总期望查询次数就是 \(4n\) 次。

这个上界作为期望次数依然不够紧，但是这里我就不讨论了。不过这个做法非常有启发性意义，我们假设用 G1 的做法进行了一轮递归，那么：

• 单个元素期望询问了 \(\frac{1}{4} \times 1 + \frac{3}{4} \times 2\) 次，即 \(\frac{7}{4}\) 次。因此总期望询问次数是 \(\frac{7}{4}n\)。
• 下标集合大小变为 \(n\)，候选值集合大小期望为 \(\frac{1}{4} n\)。

此时我们再次分析刚刚所说做法的询问次数。设单个元素期望查询次数为 \(x\)。那么有 \(\frac{1}{2}\) 的概率，\(V1,V2\) 中都有该元素，此时需要 \(2\) 次查询。有 \(\frac{1}{2}\) 的概率只有一边有，此时还需继续递归，并且当前查询次数期望是 \(\frac{3}{2}\) 的。所以可以列出方程，\(x=\frac{1}{2} \times 2 + \frac{1}{2} (\frac{3}{2}+x)\)。解得 \(x=\frac{7}{2}\)。所以总期望操作次数是 \(\frac{7}{4}n+\frac{1}{4}n \times \frac{7}{2}\) 即 \(\frac{21}{8}n\) 的。

然后就做完了。

H(?). Cycle Closing

怎么做？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？

考虑当前有一棵原图的生成树 \(T\)。发现先做 \(k=3\) 的操作是非常非常优的！\(k=3\) 的合法简单路径非常好找，不过多赘述。

为什么说它非常非常优呢？假设生成树 \(T\) 的直径为 \(d\)，那么第二次做 \(k=\lceil \frac{d}{2} \rceil\) 的操作就行了！为什么任意两点之间一定能找到一条长为 \(\lceil \frac{d}{2} \rceil\) 的简单路径呢？

定义 \(\text{dis}(u,v)\) 是 \(T\) 上 \(u\) 到 \(v\) 的简单路径上的边数（我谔谔）。现在来分类讨论（直径说的当然也是边数！）：

• 若 \(\text{dis}(u,v) \geq \lceil \frac{d}{2} \rceil\)。

这是非常酷炫的。将 \(T\) 上 \(u\) 到 \(v\) 的这一条链拿出来并将编号按顺序离散化，那么 \(i\) 和 \(i+2\) 之间是在操作一中连了一条边的。也就是说，它们之间的最短路径可以取到 \(\lceil\frac{\text{dis}(u,v)}{2}\rceil\)（最小值）。可以轻松证明 \(\lceil\frac{\text{dis}(u,v)}{2}\rceil\) 到 \(\text{dis}(u,v)\) 的任何一个路径长度都能取到，显然也能取到 \(\lceil \frac{d}{2} \rceil\)。输出路径也是容易的。

• 若 \(\text{dis}(u,v) < \lceil \frac{d}{2} \rceil\)。

这是非常谔谔的，因为我不会。

不过呢，我们发现，如果存在一个点 \(x\) 离 \((u,v)\) 在 \(T\) 上的路径距离为 \(D\) 的话，实际上我们可以构造出一条长度为 \(\text{dis}(u,v)+D\) 的路径。具体证明可以手动画一下模拟一下，只要分讨 \(x\) 是否在路径两边和 \(D\) 的奇偶性是否有特殊影响就大概可以理解了。反正我是这样理解的，呃呃。那么，能否找到一个点满足 \(D=\lceil \frac{d}{2} \rceil-\text{dis}(u,v)\) 呢？可以，geven 给我证明了，构造了一种方案，做完了。

UPD：有些地方写的有点问题。就是 \(k\) 是边数还是点数之类的。能理解就好。