Forgettable.

也不是全部都是容易被遗忘的算法。只是想写一下而已。

Dinic

我不会写 Dinic 啊。我只会写 ISAP。

其实，Dinic 就是从源点出发 BFS，然后改一下 DFS 中的 \(dis\) 判断，然后去掉 GAP 优化而已。令人谔谔。

匈牙利

我不会写匈牙利啊。我只会写 ISAP。匈牙利就是，枚举，找点，递归，打标记。标记不能边回退边清，不然一个度数很大的点可能会被遍历到很多遍，然后会扫很多遍出边，然后复杂度就错了。但是打时间戳就会好很多。令人谔谔。

无源汇上下界可行流

考虑一条边 \((u,v,L,R)\)。我们给这条边预分配 \(L\) 的流量，然后将它的容量设成 \(R-L\)，并建立一个虚拟源点 \(S\) 和一个虚拟汇点 \(T\)，加上 \((u,T,L)\) 和 \((S,v,L)\) 这两条边，然后以 \(S\) 为源点，\(T\) 为汇点跑普通最大流，然后若 \(S\) 的出边均满流，就找到了一组可行流。

为什么？

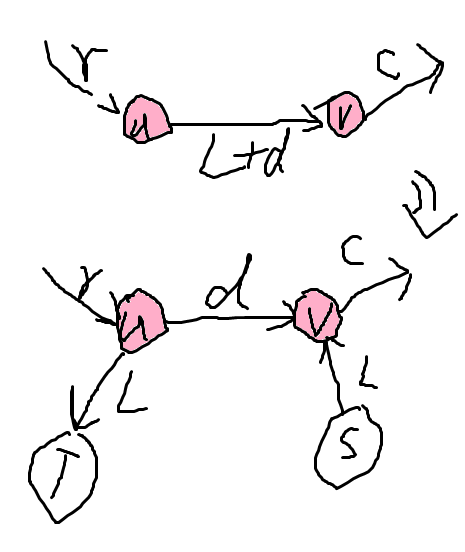
对于一条边 \((u,v,L,R)\) 来说，它在原图的大致情况是上图的上面那一部分，其中 \(r\) 是平凡的入流，\(c\) 是平凡的出流，我们知道，在这样的情况下，它们是流守恒的。然后我们建了上图的下面那一部分的那张图，容易发现，当 \((S,v,L)\) 和 \((u,T,L)\) 满流时，它们也是流守恒的。因此，任意一个原图可行流都对应一个新图最大流，反之亦然，即它们形成了一个双射，所以可以说它们是等价的。（和 \(S\) 或 \(T\) 相关的满流条件是必须满足的。）

然后有了新图，输出方案也是容易的，不阐述了。还有一些东西，不阐述了。

无源汇上下界最大流/最小流

居然网上没多少讲这个东西的文章，那我就来跟大家讲一讲。

首先，我们发现我们还没有定义无源汇网络的最大流/最小流是什么，然后再想一想，发现它们没有什么意义。所以我们就做完了。

代码实现：

有源汇上下界可行流

有源汇网络里，源点 \(S\) 和汇点 \(T\) 是不满足流守恒的。所以可以连接一条 \((T,S,\inf)\) 的边，然后就可以套用无源汇上下界可行流的做法了。容易发现，这个可行流的大小就是 \((T,S,\inf)\) 这条边的流量。

有源汇上下界最大流

先跑可行流，然后删掉 \((T,S,\inf)\)，保留残量网络的其余部分，再跑原源点 \(S\) 到原汇点 \(T\) 的最大流，这个最大流加上前面的可行流就是答案。这个是很好理解的，不要把残量想成流量就行了。

有源汇上下界最小流

我不会。等会。

Tarjan

待补。

Exgcd

待补。

Matrix-Tree

待补。

类欧几里得算法

待补。

wqs 二分

待补。

数位 DP

待补。

虚树

待补。

Splay

待补。

待补。