补题周记
越写越卡了。wxr 说得对。
A Nezzar and Hidden Permutations
怎么刻画一个二元限制?典型的,考虑在 \(l_i\) 和 \(r_i\) 间连边。如果说想要 \(p_{l_i} < p_{r_i}\),那么定向为 \(l_i\) 指向 \(r_i\),反之亦然。因此这个东西相当于给图定向。那么显然,合法的 \(p,q\) 都是定向出来这个图的拓扑序。(这里指的拓扑序不是传统意义上的拓扑序,而是每个点在拓扑排序中被遍历到的顺序。就是说 \(p_u\) 是 \(u\) 在拓扑排序中被遍历到的顺序。)也就是说,要找到两个拓扑序,使得它们的相同点值尽量少。
考虑现在有一张 \(n\) 个点的无向图。如果说现在有一个点度数为 \(n-1\),那么对于任意一种定向方式,它在 \(p,q\) 中的值一定相等。然后现在把这个点删去。如果存在度数为 \(n-2\) 的点,那么它也是必定相等的,证明均显然。由此可见,相同点值个数的下界,就是删到只剩 \(n'\) 个点且满足没有度数为 \(n'-1\) 的点时的 \(n-n'\)。可以构造出这样一种方案吗?可以的可以的。
我们现在的目的是让删后的图没有相同点值。设最后删到 \(G'\),那么其中所有的点度数必然 \(< n'-1\)。这个东西不好刻画,也不好构造方案。但如果考虑它的补图,就有如下几个性质:
- 没有孤立点。显然。
- 删边后若能构造方案,则删边前必然也能构造方案。这里需要说明。补图的删边相当于原图的加边,也就代表着更多的限制,如果在更多限制下能构造方案,更少限制下当然这个方案也合法。
- 如果它是点数 \(\geq 2\) 的菊花图,那么很好构造。设根编号为 \(x\),则 \(p_x=1,q_x=n'\)。其它节点在 \(p\) 中依次赋值 \(2 \sim n'\),在 \(q\) 中依次赋值 \(1 \sim n'-1\)。需要注意,在补图中,需要满足的限制其实是没有的边的限制,因此可以证明这个构造是对的。
大概可以猜到做法了。用若干菊花图覆盖完补图,且要求点数 \(\geq 2\)。然后不同菊花图之间点对的限制是好满足的,相同的就按上面构造,然后就做完了。
怎么分成若干菊花图是简单的。先写完题有时间再补。
A Chests and Keys(你显然能看出,很多题没在这里写。)
左边 \(n\) 个点表示宝箱,右边 \(m\) 个点表示钥匙,如果宝箱 \(i\) 需要钥匙 \(j\),就连一条 \((i,j)\) 的边。
考虑 Alice 赢的条件,枚举 Bob 打开宝箱的集合 \(S\),那么它需要的钥匙集合就是和集合 \(S\) 相连的右部点的集合,这里记作 \(N(S)\),因此,\(A(S)\) 必须 \(\leq B(N(S))\)。对于所有 \(S\),这个条件都必须满足,发现这个是东东定理。
因此,考虑建出网络流模型,源点连宝箱,宝箱连钥匙,钥匙连汇点。其中,源点到宝箱的边容量为 \(a_i\),钥匙到汇点的边容量为 \(b_i\),我们要做的,就是花 \(c_{i,j}\) 的代价在宝箱 \(i\) 和钥匙 \(j\) 中加一条容量无穷的边,并让源点连出去的边均满流,这样才能满足 Hall 定理的条件,才能让 Alice 赢。
直接状压 DP 就能做了。但是可以把它转化成一个容易理解的秋雨盒子模型。左边第 \(i\) 个盒子里有 \(a_i\) 个球,右边第 \(j\) 个盒子容量为 \(b_j\)。右边盒子最初是空的。现在要将球全部从左边转移到右边,求最小花费。
设 \(DP_{S,i,j}\) 表示右边盒子剩余容量状态为 \(S\) 时,转移完前 \(i-1\) 个盒子的球,第 \(i\) 个盒子还剩 \(j\) 个未转移时的最小代价。我好像不会 \(O(5^n n^2)\)。\(O(5^n n^2 V^2)\) 我还是会的。呃呃。
A 预处理器
题意:一个 \(n\) 个数的序列,第 \(i\) 个数值域是 \([A_i,B_i]\),且奇偶性是 \(P_i\),要求它们和在 \([S,T]\) 之间,求合法序列的数量。模数不一定是质数。
显然要 \(2^n\) 容斥。容斥之后,预分配处理奇偶性,然后组合数求和,然后就做完了。需要注意的是,组合数不能用逆元算了,直接下降幂也会爆。不过可以这样做,要求 \(\frac{\prod a_i}{m!}\),就先把 \(m!\) 用 long long 存下来,然后遍历 \(a\) 序列,每次求 \(\gcd\) 再除。反正就是,用 jr_zch 的话来说,是在模拟人类约分的过程,然后就做完了。时间复杂度 \(O(2^n n\log V)\)。
SSR 预处理器
\(n\) 可以加强到 \(30\)。这个时候就不能 \(O(2^n)\) 了。但是显然可以折半。左右两边均 \(O(2^{\frac{n}{2}})\) 处理,但我们不处理方案数,只处理需要预分配多少。那么合并就是简单的了。枚举左边预分配的值是 \(L\),右边预分配的值是 \(R\),若两边的和刚好是 \(S\)(这里都是奇偶预分配过的,即应该要除以 \(2\)),那么还有 \(S-L-R\) 个值要分配给 \(n\) 个数。方案数是 \(C_{S-L-R+n-1}^{n-1}\)。当我们枚举 \(L\) 时,这个东西显然是关于 \(R\) 的多项式。那么对于一个 \(R\),它的贡献就是代进左边所有多项式后的值的和。所以可以对左边所有多项式求和,然后代进去算。但是我们的 jr_zch 说 \(R\) 太大了的话这个组合数就不是一个多项式了,如果是这样的话,我们可以求多项式前缀和,然后就是对的了。可喜可贺。时间复杂度可能是 \(O(2^{\frac{n}{2}}n^2)\) 的吧。不清楚。实现精细貌似可以 \(O(2^{\frac{n}{2}}n\log V)\)。如果直接做的话需要模数是质数。实现精细貌似可以不需要模数是质数,多项式直接暴力展开就行了。不清楚。
B 树
sanssanssanssanssanssansTennnaamamannantTnenananwa' \WHATR THE>>>?????/HOW WOH WHAT'S HECK WHAT WHAT WHO WOH HOW MAMA MIWH HAOT HOAT HECK WHAT H9OW WHWAT WHKHW WHAT HIOLW MAMA WJHAOW HAOW WHOW AUWOAHWOW WHAT WHAWHT W HECKEHECKEHECBJ
C 最后一道
其实这不是最后一道!!!哈基米。
删点不好刻画,但是如果在黑边上加上白点,那么删点其实就是把当前的黑点和周围的白点全部合成一个白点。然后就可以发现,诶,两个黑点连通居然可以被刻画成两个黑点之间有一个白点!!!
这个事情看着很对,其实也可以归纳证明。现在把一个黑点和周围的白点合并,那么原先和它相连的黑点们现在都通过合并后的新白点相连了,的确符合操作。
现在就好做很多了。(其实也没那么好做。)首先呢,由于点 \(n\) 最后被删除,所以把点 \(n\) 设为根,这样能保证每个白点都有父节点,且其为黑点,能免去很多分讨。
然后是分讨。(对。)原来的 \((a,b,c)\) 三元组,现在可以看作 \((a,d,b,e,c)\) 五元组,其中 \(a,b,c\) 为黑点,\(d,e\) 为白点。
先考虑 \(d=e\) 的情况。看图。
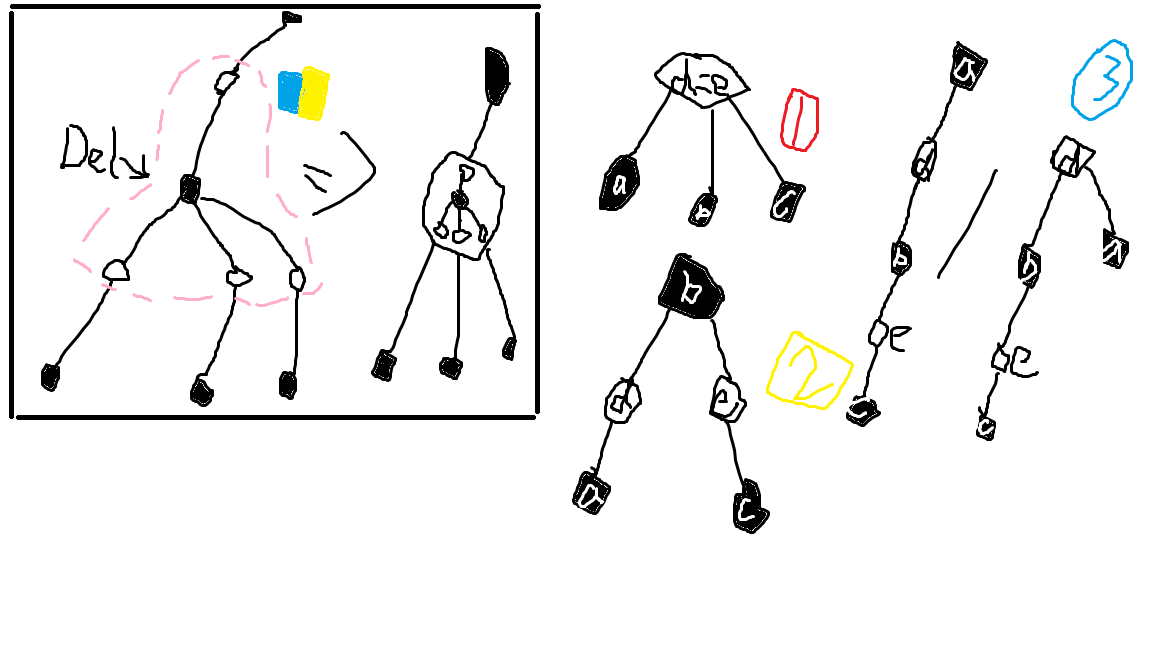
这张图其实捏他了一些东西,无奖竞猜,猜对无奖。
\(d=e\),即情况①。这个时候,我们只要处理出 \(f_u\),代表白点 \(u\) 的黑点儿子个数即可。然后我们可以知道,这种情况的贡献是 \((f_u+1)f_u(f_u-1)\)。(\(f_u+1\) 是因为 \(u\) 的父节点也是黑点,也要参加这种情况的讨论。)
\(d\neq e\),以黑点为 LCA 的双链,即情况②。这个时候,只需要枚举 LCA 和它的白点儿子,然后简单计算即可。这种情况的贡献是 \(\sum\limits_{v1\in son_u}\sum\limits_{v2\in son_u,v2\neq v1} f_{v1}f_{v2}\)。
\(d\neq e\),且不属于情况②的,即情况③。这个时候稍微有点麻烦,我们可以枚举较高的那个白点,然后处理出 \(g_u\),代表白点 \(u\) 子树内和 \(u\) 距离为 \(2\) 的白点的黑点儿子个数之和。(有点绕。)此时,它的贡献是 \(2g_uf_u\)。你会发现,情况③中的两个小图代表了我们也要考虑 \(u\) 的父节点,但是这里乘的却是 \(f_u\)。这是因为当最下方的黑点确定时,\(d\) 周围有一个黑点是不能选择的,这个很好理解,所以乘的不是 \(f_u+1\) 而是 \(f_u\)。
然后可以发现这样统计不重不漏,剩下就是实现的问题了。
Integer Game
以下是官方题解的美化版。
⾸先每个集合可以独⽴考虑,因为多个集合组成的游戏的 \(\operatorname{SG}\) 值就是每个集合各⾃的 \(\operatorname{SG}\) 值的异或。其次每个集合初始都是区间,可以证明每个集合⼀直是区间。然后计算区间 \([l,r]\) 的 \(\operatorname{SG}\) 值。
令 \([l,l-1]\) 表示空集,则 \(l-1 \leq r \leq lp\) 的时候,由于每次可以删掉区间任意后缀(即形如 \([?,r]\) 的⼦区间),\(\operatorname{SG}\) 值为 \(r-l+1\)。可以归纳证明当 \(r\) 为 \(kp+1(k\geq l)\)时,\([l,r]\) 的 \(\operatorname{SG}\) 等于 \([l,k-1]\) 的 \(\operatorname{SG}\), 除此之外的 \(r\) 按从⼩到⼤的顺序 \(\operatorname{SG}\) 值依次递增 \(1\)。\(r\leq lp\) 时命题成⽴。当 \(r\) 为 \(kp+1(k\geq l)\)时,\([l,r]\) 可以到达 \([l,k],[l,k+1],\dots,[l,kp]\) 这些状态。由归纳假设,对于所有的 \([l,j](j<k)\),\([l,jp+p+1]\) 的 \(\operatorname{SG}\) 值和 \([l,j]\) 的 \(\operatorname{SG}\) 值相同。\(jp+p+1\) 在 \(k\) 和 \(kp\) 之间,除了 \(j=k-1\) 的情况。那么在计算 \([l,r]\) 的 \(\operatorname{SG}\) 值时,可以认为 \([l,r]\) 能到达 \([l,j]\), 其中 \(l-1\leq j\leq k-2\)。即 \([l,r]\) 可以到达任意 \([l,x](l-1\leq x\leq r)\), \(x=k-1\) 除外。\(x < k-1\) 时,\([l,x]\) 的 \(\operatorname{SG}\) 值取遍了所有⼩于 \([l,k-1]\operatorname{SG}\)值的⾮负整数。\(x \geq k\)(且不超过 \(kp\))时,\([l,x]\) 的 \(\operatorname{SG}\) 值也不等于 \([l,k-1]\) 的 \(\operatorname{SG}\) 值,因为 \([l,x]\) 可以转移到 \([l,k-1]\)。这就证明了 \([l,r]=[l,kp+1]\) 的 \(\operatorname{SG}\) 值等于 \([l,k-1]\) 的 \(\operatorname{SG}\) 值。
对于另⼀种情况,我们依次考虑 \(r=kp+2,\dots,kp+p\)。当 \(r=kp+2\) 时,\([l,r]\) 能转移到的状态是所有 \([l,r-1]\) 能转移到的状态再加上 \([l,r-1]\)。即可以认为 \([l,r]\) 能转移到任意 \([l,x]\),包括刚才 \([l,r-1]=[l,kp+1]\) 不能转移到的 \([l,k-1]\),因为 \([l,r-1]\) 的sg值等于 \([l,k-1]\) 的 \(\operatorname{SG}\) 值。那么显然 \([l,r]\) 的 \(\operatorname{SG}\) 值是所有 \([l,x]\) 的 \(\operatorname{SG}\) 值之最⼤值再加 \(1\)。\(r=kp+3,\dots,kp+p\) 时,\([l,r]\) 能转移到的状态每次都⽐ \([l,r-1]\) 能转移到的状态多⼀个 \([l,r-1]\),所以每次 \(\operatorname{SG}\) 值都是 \([l,r-1]\) 的 \(\operatorname{SG}\) 值再加 \(1\)。
简化版:
先说结论,对于 \([l,r]\),且满足 \(r=kp+1\),则 \(\operatorname{SG}(l,r)=\operatorname{SG}(l,k-1)\),否则可以直接计算。
考虑归纳证明。对于 \([l,kp+1]\),一次合法的操作必定只能选择 \([k+1,kp+1]\),即它的后继状态为 \([l,k] \sim [l,kp]\)。在这些状态中,取出所谓的特殊状态 \([l,jp+1]\),它们都满足 \(\operatorname{SG}(l,jp+1)=\operatorname{SG}(l,j-1)\)。
我根本就没看懂,垃圾题目,垃圾题解。
A 方
众所周知,对于 \(f(n)=\sum\limits_{i=0}^{n-1} f(i)(n-i)^2\),我们可以用组合意义去加速,将它写成一个常系数齐次线性递推。意思就是说,\((n-i)^2\) 的意思是在 \((n-i)\) 个数中选两个数时有序数对的个数(元素可重),于是就可以设计状态 \(f_{i,0/1/2}\),表示 \(i\) 所在正方形已选择 \(0/1/2\) 个点时的方案数。
然后呢,刚刚 jr 发现它的矩阵是三阶的,所以我们来考虑代数推导。
易知,
所以,
由此可得,
然后有,
再来一次,
上两式相减,得到




 浙公网安备 33010602011771号
浙公网安备 33010602011771号