EDU 180

掉成newbie了。

A. Race

枚举可过。

B. Shrinking Array

观察发现答案只有 \(-1,0,1\) 三种。画个函数就能理解了。

C. Coloring Game

排序（geven说原序列有序）。设选的三个数分别为 \(\{a_x,a_y,a_z\}(x<y<z)\)。易得需满足条件 \(a_x+a_y > a_z\) 和 \(a_x+a_y+a_z > a_n\)。所以枚举 \(x\) 和 \(y\) 时得到条件 \(a_n - a_x - a_y < a_z < a_x + a_y\)（当然还要满足 \(a_y<a_z\)）。二分可做到 \(O(n^2 \log n)\)。发现固定 \(y\) 时，随着 \(x\) 的增大，\(a_z\) 的下界不增，上界不降，所以可以双指针做到 \(O(n^2)\)。

D. Reachability and Tree

当深度为奇数的点指向深度为偶数的点时，good pairs 对数为 \(n-1\)。考虑调整一下。仔细思考，发现当存在某一点度数为 \(2\) 时，翻转它的任意一棵子树内的所有边，就能得到 \(n\) 对 good pairs。

这个故事启示我们想题不能想太死，尤其是这种题。赛上一直在想翻转一条边就行了，然后就呃呃了。愤怒之火也是同一类型的题。就是不能想太死。

E. Tree Colorings

发现一个 beautiful coloring 当且仅当绿色点只形成一个连通块，删去绿色点后得到的若干连通块，每个只能涂一种颜色，just like this:

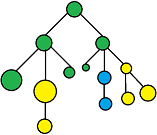
这个什么恰好 \(n\) 种方案至少需要多少个点的问法太奇怪了，直接先来看某种树有多少种方案怎么计数。设 \(T_i\) 是一棵树，\(T_j\) 是它根节点最右端的那棵子树（说法不太严谨，但是可以理解），\(f(T)\) 代表 \(T\) 这棵树 beautiful coloring 的数量，则有转移 \(f(T_i) = f(T_i-T_j)(f(T_j)+2)\)（写得不太严谨，但是可以理解）。\(+2\) 是因为 \(T_j\) 可以染色成全蓝或全黄。

现在再考虑 \(dp_i\) 代表方案数为 \(i\) 的最小点数。根据上面 \(f\) 的转移，发现方案数 \(i\) 必定由 \(d\) 与 \(\frac{i}{d}\) 相乘得到，那是不是说 \(dp_i = dp_d + dp_{\frac{i}{d}}\) 呢？不是，因为其中有一个加了 \(2\)。所以正确转移应该是 \(dp_i = \min(dp_i,dp_d+dp_{\frac{i}{d}-2})\)。要注意边界问题。初始状态当然就是 \(dp_1 = 1\) 了，根节点染色方案只有一种，其它状态都可以转移得到。每次枚举 \(i\) 与其因子，时间复杂度可以做到 \(O(n \log n)\)，但是 \(O(n \sqrt n)\) 也可以过。

UPD：哎呀。\(O(n \sqrt n)\) 看起来过不去。不过没关系。\(O(n \log n)\) 也很好写。

UPD2：好像没说，方案数为偶数时一定无解。因为任何一棵树，都存在涂全绿的 \(1\) 种方案，此外的任意一种方案蓝黄反转后仍然合法，此时方案数一定为奇数。

UPD3：顺带一提，方案数为奇数时一定有解。构造 bamboo 就可以了。

F. Variables and Operations

每个形如 \(a_{x_i} = \min(a_{x_i},a_{y_i}+z_i)\) 的操作，都可以看做一条边的松弛。即每个变量都有一个初始 \(dis\) 为 \(a_i\)，然后变量 \(y_i\) 向 \(x_i\) 连长度为 \(z_i\) 的边，这样问题就变成了一个图论问题。考虑什么样的点才是unstable的。到一个点可能有很多条最短路，一定能找到一种方案，从 \(u\) 到 \(v\) 以正确的顺序松弛一条最短路。但如果每次都先松弛连向 \(v\) 的边，那么每一条最短路都会计算错误，此时 \(v\) 的 \(dis\) 也就错了，然后就能发现 \(v\) 是unstable的。

但是这样有一个问题，如果松弛完所有连向 \(v\) 的边后最短路已经被更新正确，那么无论以怎样的顺序松弛，\(v\) 的 \(dis\) 都不会算错，此时 \(v\) 是stable的。于是可以发现，倘若到 \(v\) 所有最短路的边数均 \(\geq 2\)，那么 \(v\) 就是unstable的，否则 \(v\) 就是stable的，因为怎么松弛最短路都正确。

于是就可以处理两个数组，一个是 \(d_{i,j}\)，即 \(i\) 到 \(j\) 的最短路，一个是 \(e_{i,j}\)，即 \(i\) 到 \(j\) 的只经过 \(0\) 或 \(1\) 条边的最短路。这两个都可以 Floyd 预处理吧（不考虑点权）。因此，考虑点权后，到达 \(v\) 的最短路为 \(\min_{j=1}^n d_{j,v}+a_j\)，到达 \(v\) 的只经过 \(0\) 或 \(1\) 条边的最短路为 \(\min_{j=1}^n e_{j,v}+a_j\)。你可能以为这没有考虑 \(a_v\)，但其实它考虑了。所以，若 \(\min_{j=1}^n d_{j,v}+a_j = \min_{j=1}^n e_{j,v}+a_j\)，则 \(v\) 是stable的，否则它是unstable的。

现在考虑怎么让 \(\min_{j=1}^n d_{j,v}+a_j < \min_{j=1}^n e_{j,v}+a_j\) 从而让 \(v\) 变得unstable。发现因为是要 \(\min\) 最小，所以显然 \(k\) 次操作全部减在一个点上更优。现在，尝试算出 \(lim_{i,j}\) 代表通过减小 \(a_j\) 让 \(i\) unstable需要的最小操作次数。若 \(d_{j,i} = e_{j,i}\)，那无论怎么减小 \(a_j\)，\(d_{j,i} + a_j\) 都会等于 \(e_{j,i}+a_j\)，也就是说不可能让原来stable的 \(i\) 变得unstable。

否则，只需要减小 \(a_j\) 使 \(d_{j,i}+a_j < \min_{j=1}^n e_{j,v}+a_j\) 就行了。因为此时 \(d_{j,i}<e_{j,i}\)，所以减小 \(a_j\) 并不会让 \(e_{j,i}+a_j\) 影响结果。那么，只需要预处理出 \(\min_{j=1}^n e_{j,v}+a_j\) 就能算出 \(lim_{i,j}\) 了，然后就做完了。