补题日记

20250621-A-愤怒之火

q12ue2.1s
确实愤怒了。
结论：以一个度数 \(\geq 2\) 的点作为根节点，并把所有非叶子节点放到叶子节点上。如果非叶子节点个数大于叶子节点个数，则无解。

为什么？

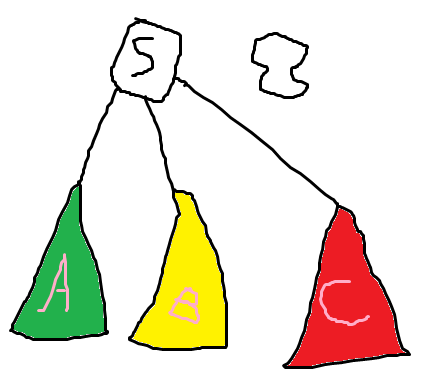
考虑度数 \(\geq 2\) 的点 \(S\)，删去它一定会形成至少两个连通块。考虑 \(u \in A\) 和 \(v \in B\)，那么在新树上，它们应该位于 \(S\) 的同一子树再考虑 \(u \in A\)，\(v \in B\) 和 \(u2 \in A\)，因为 \(u\) 和 \(v\) 在同一子树，又因为 \(u2\) 和 \(v\) 在同一子树，所以 \(u\) 和 \(u2\) 在同一子树。所以可以证明，\(A,B,C\) 中的所有点，都应该在 \(S\) 的同一子树内，那 \(S\) 就只可能是叶子节点。

20250621-B-勾股计数

把 \(a^2 + b^2 = c^2\) 变成 \(a^2 = c^2 - b^2\)。

所以 \(a^2 = (c-b)(c+b)\)。设 \(A=c-b,B=c+b\)。问题就变成了求 \(a^2\) 的因子 \(d\) 的个数，且 \(d \neq a\)，\(d \equiv \frac{a^2}{d} \pmod 2\)，\(d < \frac{a^2}{d}\)。
容易发现限制 \(1\) 和限制 \(3\) 都是好解决的，最后稍微处理一下就行了，比较麻烦的是限制 \(2\)。尝试对 \(a^2\) 进行质因数分解，得到 \(a^2 = \prod 2^{2sr}p_1^{2r_1}p_2^{2r_2} \dots p_k^{2r_k}\)。因为要两个因子奇偶性相同，所以按是否有 \(2\) 来分讨。

• 若没有 \(2\)。

质因数爱怎么分怎么分，反正都是奇数。每个质因子都可以给 \(d\) 放 \(0 \sim 2r_i\) 个，因此总方案数为 \(\prod (2r_i + 1)\)。

• 若有 \(2\)。

无论怎么分都至少有一个偶数。因此要满足条件必须两个都是偶数，即 \(2\) 先预分配两个，剩下 \(2sr-2\) 个随便分，有 \((2sr-1)\) 种方案。因此总方案数为 \((2sr-1)\prod (2r_i+1)\)。

发现答案就是这个函数的前缀和。并且这个函数是积性函数。而且质数点值和超级好求。Min_25 筛即可解决。

20250621-C-乱斗之星

20250701-A-置换

打爆了。T1 前前后后浪费了我起码一个半小时。本来是个简单题，但是我忘了自然数幂和怎么 \(O(k)\) 求了。

20250701-B-求和

这个式子一看就非常根号分治。首先，直接暴力复杂度是 \(O(q \times \frac{n}{k})\) 的，\(k\) 较大的时候可以这么做。
\(k\) 较小时做法也不难，设 \(g(x,r)\) 为某个 \((x,r)\) 询问对应的答案，然后将杨辉三角左对齐，发现要求的是第 \(x\) 列的某些点值的和。这个 \(g\) 是可以转移的。删掉杨辉三角第 \(0\) 行和第 \(0\) 列，进行观察。

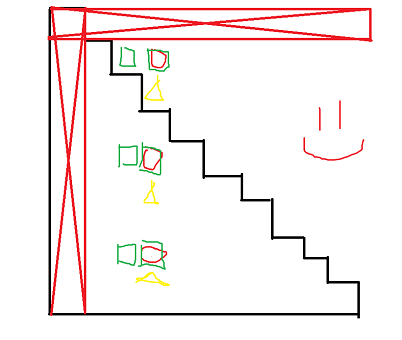
假设现在已知前面的列的答案和圆圈部分的和，现在要求三角形部分的和。可以把其拆成正方形部分的和，然后发现这些都求过了，于是可以 \(O(1)\) 递推。
但是实际上初值是不知道的，不过根据组合恒等式 \(\sum\limits_{i=x}^n C_i^x = C_{n+1}^{x+1}\)，可以把初值设成未知数 \(a\)，然后每个值都能用其表示，然后它们和为这个东西，然后解一下方程就做完了。这个组合恒等式可以用杨辉三角推，要记牢。

这部分复杂度是 \(O(nk)\) 的。平衡一下发现 \(k=\sqrt q\) 最优。做完了。

20250701-C-BST

首先得知道怎么 \(O(n \log n)\) 建BST，一个点被插入时，它的父节点只可能是前面被插入的点中它的值域上的前驱与后继，这个前驱记为 \(pre\)，后继记为 \(lst\)，则如果 \(pre\) 被插入的时间晚于 \(lst\)，那么当前点为 \(pre\) 的右儿子，否则它为 \(lst\) 的左儿子。证明略。其实反证挺好证，需要注意到性质要么 \(pre\) 在 \(lst\) 左子树内，要么 \(lst\) 在 \(pre\) 右子树内。

这个题的值域是排列，所以少了很多分讨。

首先呢，可以发现 \(\sum dep = \sum siz\)，这是一步简单的转化（根节点深度为 \(1\)）。然后呢，发现这个东西和值域有很大关系，将这个数列按值域排序，得到下图：

其中，红三角形代表这个值位于 \([a_1\sim a_{l-1}]\)，绿方形代表这个值位于 \([a_l\sim a_r]\)，黑圆圈代表这个值位于 \([a_{r+1}\sim a_n]\)。首先考虑黑圆圈，当它们被加入的时候，它们的连边方式不可能跨越绿点或红点（姑且这么称呼吧），因此可以发现，一段连续的黑圆圈可以构成一棵确定的子树，然后其根连在哪可能确定可能不确定。具体而言，如果说一段黑点位于两个红点间，那它的根必定是这两点间后加入那个的儿子。如果位于一个红点一个绿点间，它的根的父节点必定是绿点。如果位于两个绿点间，无法确定。

不过呢，这样就已经可以算出黑点的 \(\sum siz\) 和黑点对红点的贡献了（先不考虑情况二）。当然最开始把红点拎出来建树也能算出红点对红点的贡献。

下一步，将黑点变成一棵棵子树后。

将一段连续的绿点与黑子树拿出来（如图绿色梯形部分），这一段显然也构成一棵子树，并且能知道它挂哪。因此，现在也能算出绿点对红点的贡献（当然黑点对红点的贡献最好在这里一起算）。

现在，只缺绿点的 \(\sum siz\) 了，也就是缺绿点的树形态。将绿点编号离散化，只考虑绿点如何变成一棵树。假设点 \(k\) 是根节点，发现选择它过后，它右边的点不可能选择它左边的点做父节点，它左边的点同理。即它的左右两边又是两棵独立的子树。这启示我们使用区间 DP。设 \(dp_{l,r}\)，表示考虑只 \([l,r]\) 这段绿点时绿点的 \(\sum siz\)。转移是简单的，前缀和优化可做到 \(O(n^3)\)。四边形不等式决策单调性优化可做到 \(O(n^2)\)。

20250701-D-最小最大

有结论，\(\min\) 与 \(\max\) 确定时，若存在合法树则其形态唯一。把 \([\min,\max]\) 的点设成 \(1\)，其余设成 \(0\)，那这棵合法树就是包含 \(\min\) 和 \(\max\) 的极大 \(1\) 连通块。证明不难，基于此有 \(O(n^2\log n)\) 的并查集做法。

求的是 \(\sum \min \times \max \times siz\)，可以考虑拆贡献。枚举一个点 \(x\)，求合法树包含它的所有 \((\min,\max)\) 二元组的 \(\sum \min \times \max\)，所有 \(x\) 的 \(\sum\) 求和即是答案。发现合法就是说，\(\min,\max,x\) 三个点的生成子树（啥玩意）上的权值都在 \([\min,\max]\) 之间。画图发现这其实是一个路径上的问题，考虑淀粉质。淀粉纸。点份只。点分治。

然后这个东西它其实是一个双指针+线段树，然后可以做到 \(O(n\log^2 n)\)。（没写完）

继续继续。假设现在有分治中心 \(y\)，设 \(mx_i\) 代表节点 \(i\) 到 \(y\) 路径上编号最大的点的编号，\(mn_i\) 代表节点 \(i\) 到 \(y\) 路径上编号最小的点的编号。那么 \((\max,\min,x)\) 合法需要满足如下限制。

• \(mx_{\max}=\max,mn_{\max} \geq \min\)。
• \(mx_{\min} \leq \max,mn_{\min}=\min\)。
• \(mx_x \leq \max,mn_x \geq \min\)。

下文称满足 \(mx_x=x\) 的点为 \(1\) 类点，满足 \(mn_x=x\) 的点为 \(2\) 类点。现在，将 \(2\) 类点作为 \(\min\) 从大到小考虑，则关于 \(1\) 类点和 \(x\) 的限制会逐渐放宽，这个可以双指针处理。设 \(a_i\) 在 \(1\) 类点 \(i\) 有效时值为 \(i\)，否则值为 \(0\)，\(b_i\) 为有效的且 \(\max\) 为 \(i\) 时能使用的 \(x\) 的个数，则对于一个 \(\min\)，所求答案为 \(\min \times \sum a_ib_i\)。双指针已经可以满足 \(mn_{\min}=\min,mx_{\max}=\max,mn_{\max} \geq \min,mn_x \geq \min\) 这些限制了，剩下的限制只需要线段树维护 \(\sum a_ib_i\) 就可以了，这是简单的。然后就做完了。

20250703-A-Count Set

发现在 \(n\) 个点的环上选 \(k\) 个不相邻的点方案数为 \(C_{n-k-1}^{k-1} + C_{n-k}^k\)，然后做卷积就可以了。可以用分治 NTT 实现，也可以用神奇的堆合并果子做法。时间复杂度均为 \(O(n \log^2 n)\)。合并果子可能常数小些，没有严谨分析过。

20250703-B-Shattrath City

只要 dp 状态设对了，这个题就很简单了。设 \(f_i\) 表示当前只有 \(i+n-1\) 个点且 \([i,i+n-1]\) 是当前的第一个 \(1 \sim n\) 的排列的方案数。这个东西可以容斥计算，具体来说：

\(f_i = n!\times n^{i-1} - \sum\limits_{j=i-n}^{i-1} f_j(i-j)! - \sum\limits_{j=1}^{i-n-1} f_jn!n^{i-j-n}\)

首先，\(n! \times n^{i-1}\) 是总方案数，后面减去的东西是不合法方案数，就是前面已经出现过 \(1 \sim n\) 的排列的方案数后面那个很好理解。假如这两个排列没有交集，后面的排列当然可以随便填，只要是个排列（有系数 \(n!\)），中间的空位更是可以随便填（有系数 \(n^{i-j-n}\)）。如果有交集就是前面减去的这个东西了，画图分析发现，有 \((i-j)\) 项是固定了值但没有固定好位置，其余项既固定了值又固定了位置，所以有系数 \((i-j)!\)。

直接分治 NTT 当然可以做到 \(O(n \log^2 n)\)，但是使用一些解方程和生成函数技巧（主要是移项），可以做到 \(O(n\log n)\)。

20250703-C-Gilneas

疑似有点诈骗了。这个期望可以这样统计：对于每个操作，算出它能修改的并且能保留到最后的期望边数，再乘上操作权值，求和。

不能保留只可能是被后面的操作修改了，所以从后往前枚举操作。一条边不被修改的概率，就是能影响到它的操作的 \(\prod(1-p_i)\)。然后发现一个操作要修改的是这么一些边：

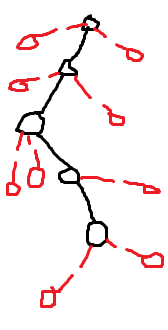
这个好像不是很做得了？不过发现把权值挂在边上本身就是一个很呃呃的事情，简单分讨发现完全可以把权值挂在每条边的父节点上，因为可以发现每个点的连向子树的边的权值必然相等。所以树剖就可以 \(O(n\log^2 n)\) 做了，查询要处理一下，要从给定节点的父节点查询。

Bonus：如果操作都是在普通的链上，怎么做？发现修改操作只多了一条不能被父节点表示的边，是否能特殊处理？我不会，会的人私信我。

20250703-D-Connectivity of Erdős-Rényi Graph

呃呃。

省选联考 2025 D1T2-追忆

重新整理一下现在要做什么。\(n\) 个点 \(m\) 条边的 DAG（\(n\leq 10^5,m\leq 2\times 10^5\)），排列 \(a\)，排列 \(b\)，\(q\) 次操作。操作 \(1\) 是交换 \(a_x\) 和 \(a_y\)，操作 \(2\) 是交换 \(b_x\) 和 \(b_y\)，操作 \(3\) 是询问满足 \(l \leq a_y \leq r\) 且 \(x\) 能到达的 \(y\) 中 \(b_y\) 的最大值。

首先，DAG 的可达性是必须得知道的。因此，使用 bitset 在 \(O(\frac{nm}{\omega})\) 的时间复杂度内求出 \(To_x\) 表示 \(x\) 能到达的点是简单的。现在来考虑 \(l \leq a_y \leq r\) 的限制，倘若已经预处理出 \(Ba_i\)，表示 \(\{y|a_y\in[i,n]\}\)，那么显然 \(Ba_l \oplus Ba_{r+1}\) 就是满足条件的点集。但是呢这样修改操作复杂度就直接爆了，为 \(O(n)\)。

没有什么其它太好的思路，考虑值域分块，设块长为 \(B\)，那么 \(Ba_i\) 表示 \(\{y|a_y \in [(i-1)B+1,iB]\}\)，预处理应该可以做到 \(O(\frac{n}{B}(\frac{n}{\omega}+B))\) 即 \(O(\frac{n^2}{B\omega}+n)\)。每次查点集时整块直接异或，复杂度 \(O(\frac{n}{\omega})\)，散块暴力，复杂度 \(O(B)\)。

将得到的点集 & 上 \(To_x\) 就是同时满足两个限制的点集，设为 \(U\)。那么如何查找 \(\max b_y\) 呢？好像也不太好找，考虑二分答案。倘若已经预处理出 \(Bb_i\)，表示 \(\{y|b_y \in [i,n]\}\)，那么显然，若 \(U\) & \(Bb_{Mid}\) 不为空，就说明合法点集中至少有一个点 \(b\) 值 \(\geq Mid\)。但是呢这样修改操作复杂度就直接爆了。所以考虑值域分块，设块长为 \(C\)，同 \(Ba\) 类似处理，先二分出最大的有合法 \(b\) 值的那个块，再在块里暴力找，时间复杂度 \(O(\frac{n}{\omega}\log \frac{n}{C}+C)\)。

修改操作直接对每个块暴力修改就行了，时间复杂度 \(O(\frac{n}{B})\) 或 \(O(\frac{n}{C})\)。

最优块长暂未分析。代码暂未实现。

UPD：已过。块长取的 \(B=500\) 和 \(C=1000\)，很可能不是最优块长。

也许是举一反三？-Range Reachability Query

20230830-20250705-cycle

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!值得铭记。

20230830-20250705-poker

呃呃，呃。

20230830-20250705-meat

四元环计数。

20230830-20250705-seq

神秘分块。

[伯明翰20250708]灯佳和郊奂

ぼみんはん。

乱搞な了 \(70pts\)，相同しる的 geven 拿了 \(100pts\)，因为他会写 fread，下去我也要背。

正解很智慧。先枚举一个 \(a\) 的前缀 \(A_i\)，并找到 \(b\) 的满足 \(\leq A_i\) 的最长前缀 \(B_j\)。那么若 \(A_i-B_j=0\)，显然可以直接输出这两个前缀。否则，容易证明它们的差在 \([1,n-1]\) 之间，又因为这样的前缀有 \(n\) 组，根据げちゃお原理，必定有至少两组前缀差值相等，然后画图就能发现它们之间是一种合法方案。具体地，若 \(A_{i1}-B_{j1}=A_{i2}-B_{j2}\)，なめ显然，\(A_{i2}-A_{i1}=B_{j2}-B_{j1}\)。然后就能输出了。

值得一提的是，如果一个数列的和太小，那么两组前缀的差可能 \(\geq n\)，但容易发现，这样交换两个数列再做一遍就是对的了。

[伯明翰20250708]圣诞派派翁

しだんぱいぱいうん。

首先，将问题转化为一个聪明的网络流模型。见图。

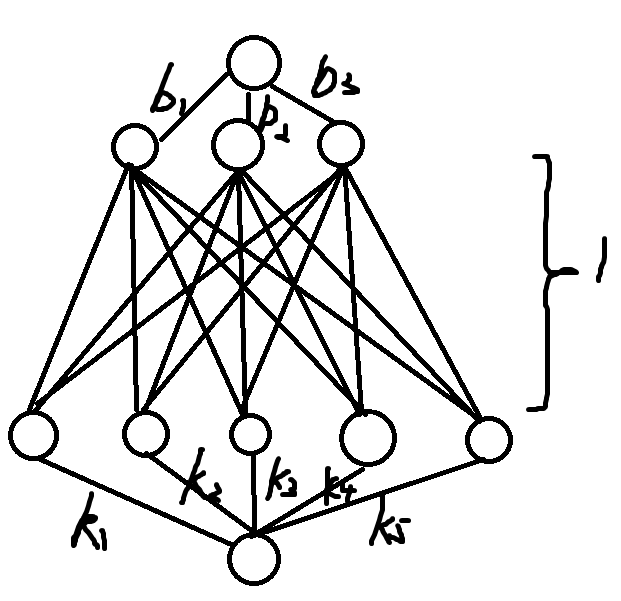
\(b\) 就是数列，\(k\) 是做减法的操作的参数。容易发现答案就是其最大流。但是这个东西不好求，考虑求它的最小割。枚举割掉了几条 \(k\) 边，容易知道 \(k\) 边一定是割前 \(i\) 小的，那么有式子 \(ans=\min_{i=0}^m pre_i + \sum\limits_{j=1}^N \min(b_j,m-i)\)。要对每个添加操作后的数列求。根据简单观察，随着数的添加，决策点 \(i\) 一定是单调不减的，同时，若决策点是 \(i\)，当前进行了前 \(j\) 次添加操作，那么可以 \(O(1)\) 地做 \(w(i,j)\) 的指针移动（就像莫队一样），因此，用整体二分复杂度可以做到 \(O(n\log n)\)。

[伯明翰20250708]我真的极了

值域倍增分块建线段树，均摊下来复杂度是对的。

具体见 https://www.luogu.com.cn/problem/P7447。

[模拟赛20230824] - 20250710 - 猫捉老鼠

终于做出来一道 T1 了，蕾姆れむ，，，

[模拟赛20230824] - 20250710 - 格斗大赛

呃。智慧题。

[模拟赛20230824] - 20250710 -大脑过载

李超树。如果要维护二次函数，那么检查一下式子能不能通过换元等方法化简之类的。

[模拟赛20230824] - 20250710 - 龙了个龙

你们记得那道题吗？就是统计有几个区间所有元素都恰好出现了 \(0\) 或 \(3\) 次的那道题？
这个题就是那道题的削弱版，使用异或哈希+莫队即可。
https://codeforces.com/contest/1418/problem/G。

写的有点水。

1 堆

题意：内部题目。滑动窗口删最大，奇加偶减，求 \(sum\)。

如果像题目说的那样先删后加，没有什么性质，但如果先加后删，就可以发现 \(\max\) 单调不增，指针维护就可以了。

2 矩阵

题意：内部题目。NOIP 2017。自己查。

将原矩阵分成 \(n\) 个长为 \(m-1\) 的行和 \(1\) 个长为 \(n\) 的列。每个序列需要维护的操作是删掉第 \(k\) 个数和在末尾加一个数。可以使用线段树软删除，维护 \(01\) 序列并线段树二分。这样就能知道每次软删除掉的数的下标了，然后暴力模拟就行了。

3 市场

不平凡的操作只有除法操作一个。可以这样处理：
定义线段树节点 \(p\) 所管辖区间值的极差为 \(M_p\)。
定义势能函数为 \(\sum\limits_p \log(M_p)\)。
那么，假设现在对 \([l,r]\) 这个线段树节点 \(p\) 管辖的区间做除法操作。
若 \(M_p=0\)，直接区间改。
若除法操作后，\(M'_p = 0\)，直接区间改。
若 \(M_p = 1\)，且除法操作后，\(M'_p=1\)，直接区间加。
否则两边递归再 PushUp。
容易发现，大多数情况下节点 \(p\) 极差至少除以二，则其势能函数至少减 \(1\)，少数情况下极差不能除以二，这个时候我们进行了 \(O(1)\) 处理。

而原始序列带来的势能是 \(O(n\log V)\)，每次区间加会将 \(O(\log n)\) 个节点的势能重置成 \(O(\log V)\)，则时间复杂度为 \(O(n \log V+q\log n\log V)\)。

4 老题重做

容易发现将点 \(i\) 右上角的点单独拿出并按横坐标排序后，满足条件的点 \(j\) 的个数即为这些点的纵坐标前缀最小值的个数。扫描线+楼房重建线段树维护即可。

5 小明的树

这个题质量比较高。
因为要求美丽时刻的点亮点的连通块数量之和，先考虑什么时候一棵树是美丽的。
首先可以发现，若一棵树美丽，当且仅当所有未点亮的点的父节点也未点亮。但是这个没啥用。
进一步地，若一棵树美丽，当且仅当未点亮的点形成一个连通块。
找一些性质。树上随便选一些点，它们一定构成一个森林。并且，其连通块数量等于其点的数量减去边的数量。
那么，时刻 \(i\)，未点亮点的个数是 \(n-i\)，若两端均为未点亮点的边的数量是 \(n-i-1\)，则这个时刻树是美丽的。

怎么维护？这相当于维护一个序列，下标 \(i\) 的初值为 \(n-i\)。设 \(time_u\) 是 \(u\) 被点亮的时刻，那么边 \((u,v)\) 两端均未点亮的时间段为 \([1,\min(time_u,time_v)-1]\)，因此这条边就应该给序列的 \([1,\min(time_u,time_v)-1]\) 这个区间减一。最后序列上值为 \(1\) 的下标对应的就是美丽时刻。线段树显然可以维护，边修改操作也很容易。

现在要求美丽时刻时点亮点的连通块数量之和，也是类似的，不细说了。就类似于有一个序列 \(a_i\)，且 \(a_i \in \{0,1\}\)，然后有一个序列 \(b_i\)，求 \(\sum\limits_{i=1}^n a_ib_i\)。线段树能做。

6 区间切割

这个题也太妙了！首先

A Appleman and Tree

苹果男人和树。

B [HAOI2015] 树上染色

树形背包。

C Colorful Tree

待补。

D Ribbons on Tree

首先，一个大小为 \(2n\) 的连通块乱连接彩带，方案数是 \((2n-1)!!\)。
然后，这个题显然需要容斥。设 \(dp_{u,j}\) 表示 \(u\) 子树内有至少 \(j\) 条边未被覆盖的总方案数，可以简单类树形背包转移。这个至少是二项式反演的至少，设 \(f(i)=dp_{1,i}\)，\(g(i)\) 是恰好 \(j\) 条边未被覆盖的方案数，那么有 \(f(n)=\sum\limits_{i=n}^N C_i^n g(i)\)，得 \(g(n)=\sum\limits_{i=n}^N (-1)^{i-n}C_i^n f(i)\)。答案是 \(g(0)\)，所以 \(ans=\sum\limits_{i=0}^N (-1)^i f(i)\)。如果想在转移后乘上容斥系数，刚刚所说的类树形背包复杂度就是 \(O(N^3)\)，因为要记录边数。但发现此题容斥系数异常简单，所以转移断边的时候乘上 \(-1\) 就行了，不再记录边数，复杂度 \(O(N^2)\)。

E Donation

发现结论：每个点如果要捐赠，必定在到达其的最后一次进行捐赠。
证明：不考虑初始钱数 \(< \sum\limits B_i\) 的情况，则每次到达一个点都必定能捐赠。那么，若同时经过一个点两次，在后一次捐赠一定更优，因为中间去别的点的时候钱数变多了，自己又不受影响。

这个应该是容易发现的。那么限制转化为，在点 \(u\) 的每个时刻，当前钱数都必须 \(\geq \max(A_u-B_u,0)\)。这里设 \(C_u = \max(A_u-B_u,0)\)。

很难发现，可以倒着来做。即，第一次走到点 \(u\) 时，需满足当前钱数 \(x \geq C_u\)，然后可以获得 \(B_u\) 的钱，并走到其它点，最后要求所有点都被访问过。模拟一下发现很有道理。这样也解决了一大难题：正着做的时候很难贪心，但是这样的话按 \(C_u\) 从小到大走显然是对的，因为得到的代价是正的，可以满足更多限制。

遗憾的是，有时会强制经过一些大的 \(C_u\)。但是发现一个事情，现在想维护的是与当前终点连通的权值小于等于某个数的点，这个显然能用 Kruskal 重构树做，放到转化后的问题上也很正确：每次解锁一个新的点，它的子树肯定就都能走了。

但如果每次枚举一个终点再去做，复杂度至少是 \(O(n^2)\) 的。然后可以用 DP，直接设 \(dp_u\) 表示从某个节点出发，走完 \(u\) 子树所有点的最小初值。设根节点为 \(rt\)，则 \(ans=dp_{rt}+\sum\limits B_i\)。这个也是说得通的，在原问题上，\(\sum\limits B_i\) 是一定要花的，所以实际上是在使最后剩余钱数最少。倒着做时这里的最小初值当然就是最小剩余钱数了。

那这个 DP 怎么做呢？设 \(Bsum_u\) 是 \(u\) 子树里 \(B\) 的和，那么叶子节点时 \(dp_u=C_u\)，否则枚举 \(u\) 的儿子 \(v\)，从 \(v\) 走上来需要的最小初值是 \(\max(f_v,C_u-BSum_v)\)，后面的是能到达点 \(u\) 所需的最小初值。到达点 \(u\) 后就可以去其它子树了，所以 \(dp_u = \min\{\max(f_v,C_u-BSum_v)\}\)。这个 DP 其实相当简单，但是我不小心忘了重构树的性质，就又看了题解。

F Fedor Runs for President

没看题解。口胡一下。

考虑环上的点变成若干子树，那么增加的简单路径就是位于不同子树的点对数量。这个不好刻画，考虑让位于相同子树点对数量最小，那么画图可以发现，新边连接两个叶子一定是最优的。

完了不会了，看题解吧。

我生气了。

上述结论都没错，考虑怎么让子树 \(siz\) 平方和最小。加边操作可以刻画成，选择一条树上路径，删掉路径上的边，使形成的若干棵新树的 \(siz\) 平方和最小。

考虑 \(dp\)。设 \(dp_u\) 表示路径从 \(u\) 延伸到一个叶子时 \(siz\) 的最小平方和。那么 \(dp_u = \min\{dp_v+(siz_u-siz_v)^2\}\)。这是单链，直接暴力枚举根可以做到 \(O(n^2)\)。如果枚举两条单链合成一个双链，设双链的答案为 \(g_u\)，就有式子 \(g_u = \min\{dp_{v1}+dp_{v2}+(siz_u-siz_{v1}-siz_{v2})^2\}\)。拆式子得到 \(dp_{v1}+dp_{v2}+{siz_u}^2 + {siz_{v1}}^2 + {siz_{v2}}^2 - 2siz_{v1}siz_u - 2siz_{v2}siz_u + 2siz_{v1}siz_{v2}\)。枚举 \(u\) 和 \(v1\) 过后，这是一个形如 \(y=kx+b\) 的形式，现在要求最小值，使用李超线段树维护。如果 \(v1\) 取到了 \(v1\) 的直线怎么办呢？i_love_xqh 说可以单点查了这个点再把它的直线加进去。于是这样就是 \(O(n\log n)\) 的了。

G Labeling the Tree with Distances

这是啥啊。

显然要用集合哈希！！！但是不能用 Xor 哈希了，这个维护 \(depth\) 的换根 Xor 哈希不好做。。。考虑另一种哈希方式，\(Hash_T=\sum\limits_{i=1}^n cnt_i base^i\)，其中 \(cnt_i\) 代表有根树 \(T\) 中深度为 \(i\) 的点的个数。然后换根就很简单了。然后剩余部分都很简单了。

J 树上 K 级祖先

学习长链剖分。

首先，和重链剖分类似的，找到每个点的长儿子，然后形成若干条长链。具体的，设 \(g_u\) 是 \(u\) 子树内深度最深的那个点的深度，那么 \(u\) 的长儿子就是 \(u\) 的子节点中 \(g\) 最大的。

预处理出 \(f_{u,i}\) 表示 \(f\) 的 \(2^i\) 级祖先，时间复杂度 \(O(n\log n)\)。

对于每条长链，设其长度为 \(len\)，预处理出其链顶向上的 \(len\) 个点和其链顶沿链向下的 \(len\) 个点的编号，时间复杂度 \(O(n)\)。

现在假设要查 \(u\) 的 \(k\) 级祖先，设 \(k\) 的 \(\text{highbit}\) 为 \(2^h\)，那么先跳到 \(u\) 的 \(2^h\) 级祖先 \(u'\)。此时 \(u'\) 必定有一个 \(2^h\) 级儿子 \(u\)，因此它所在这条长链的长度必定 \(\geq 2^h\)。现在设 \(k'=k-2^h\)。直接从 \(u'\) 跳到长链顶，若发现跳多了，就说明 \(u\) 的 \(k\) 级祖先就在这条长链上，算一算向下找即可。否则 \(k'\) 必定小于 \(u'\) 所在长链长度，跳到链顶后需要的增量就更少了，因此算一算过后发现我们一定预处理过，直接向上找就可以了。如果将 \(\text{highbit}\) 也预处理，那么查询时间复杂度是 \(O(1)\) 的。

A Nezzar and Hidden Permutations

怎么刻画一个二元限制？典型的，考虑在 \(l_i\) 和 \(r_i\) 间连边。如果说想要 \(p_{l_i} < p_{r_i}\)，那么定向为 \(l_i\) 指向 \(r_i\)，反之亦然。因此这个东西相当于给图定向。那么显然，合法的 \(p,q\) 都是定向出来这个图的拓扑序。（这里指的拓扑序不是传统意义上的拓扑序，而是每个点在拓扑排序中被遍历到的顺序。就是说 \(p_u\) 是 \(u\) 在拓扑排序中被遍历到的顺序。）也就是说，要找到两个拓扑序，使得它们的相同点值尽量少。

考虑现在有一张 \(n\) 个点的无向图。如果说现在有一个点度数为 \(n-1\)，那么对于任意一种定向方式，它在 \(p,q\) 中的值一定相等。然后现在把这个点删去。如果存在度数为 \(n-2\) 的点，那么它也是必定相等的，证明均显然。由此可见，相同点值个数的下界，就是删到只剩 \(n'\) 个点且满足没有度数为 \(n'-1\) 的点时的 \(n-n'\)。可以构造出这样一种方案吗？可以的可以的。

我们现在的目的是让删后的图没有相同点值。设最后删到 \(G'\)，那么其中所有的点度数必然 \(< n'-1\)。这个东西不好刻画，也不好构造方案。但如果考虑它的补图，就有如下几个性质：

• 没有孤立点。显然。
• 删边后若能构造方案，则删边前必然也能构造方案。这里需要说明。补图的删边相当于原图的加边，也就代表着更多的限制，如果在更多限制下能构造方案，更少限制下当然这个方案也合法。
• 如果它是点数 \(\geq 2\) 的菊花图，那么很好构造。设根编号为 \(x\)，则 \(p_x=1,q_x=n'\)。其它节点在 \(p\) 中依次赋值 \(2 \sim n'\)，在 \(q\) 中依次赋值 \(1 \sim n'-1\)。需要注意，在补图中，需要满足的限制其实是没有的边的限制，因此可以证明这个构造是对的。

大概可以猜到做法了。用若干菊花图覆盖完补图，且要求点数 \(\geq 2\)。然后不同菊花图之间点对的限制是好满足的，相同的就按上面构造，然后就做完了。

怎么分成若干菊花图是简单的。先写完题有时间再补。