Splay && LCT

Splay 是一种平衡二叉搜索树，它很平衡（存疑），并且中序遍历的值是有序的。
就像 LCT 的核心操作是 access（阿克涩斯，访问）一样，Splay 的核心操作是 Splay（伸展），它保证了 Splay 时间复杂度正确。为了区分 Splay（树）和 Splay（伸展），本文将用粗体 Splay 表示操作。

Splay 分为两种，一是左旋，二是右旋。

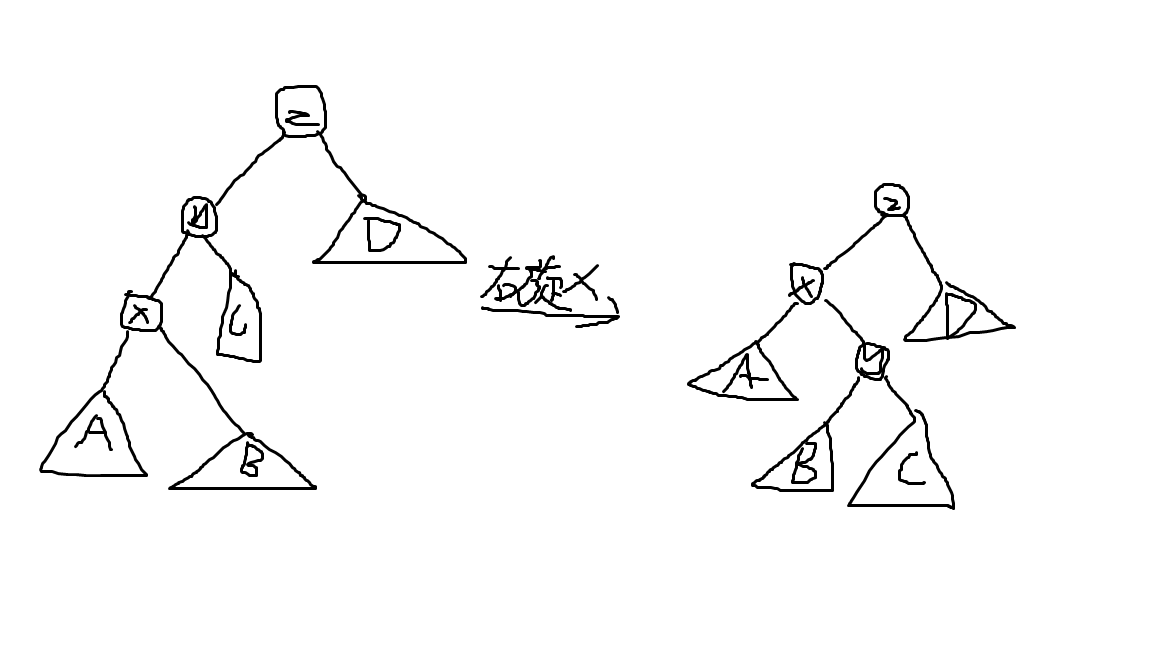
Splay \(x\) 的时候，实际上是在把它往上跳一级祖先。而这个跳的时候用左旋还是右旋，实际上就是看它是它父亲节点的右儿子还是左儿子。而且，Splay 二叉搜索树的结构还不能被破坏。（可以看图理解。）

具体地，可以将其拆分成以下几个步骤（以右旋为例，左旋对称）：

1.\(y\) 的变化：\(fa_y\) 变成 \(x\)，\(son_{y,0}\) 变成 \(B\)。
2.\(x\) 的变化：\(fa_x\) 变成 \(z\)，\(son_{x,1}\) 变成 \(y\)，\(fa_B\) 变成 \(y\)。
3.\(z\) 的变化：\(son_{z,0}\) 变成 \(x\)。
4.pushup(y),pushup(x);

实现时，要避免对 \(0\) 节点的修改，以免出现边界问题。

事实上，上文只是 rotate 的过程，并不是真正的 Splay。Splay 操作要将 \(x\) 一路 rotate 到根。具体地，我们有六种操作，zig、zag、zig-zig、zag-zag、zig-zag、zag-zig。（zig 代表左旋，zag 代表右旋。）

可以看一看应该在什么时候用哪种适合的操作。

Q：为什么不能 zag(x),zag(x);？
A：势能分析分析出来复杂度是错的。也可以直接看一条长链的情况，zag(x),zag(x); 出来仍然是一条链，但 zag(y),zag(x) 则不是。见下图。

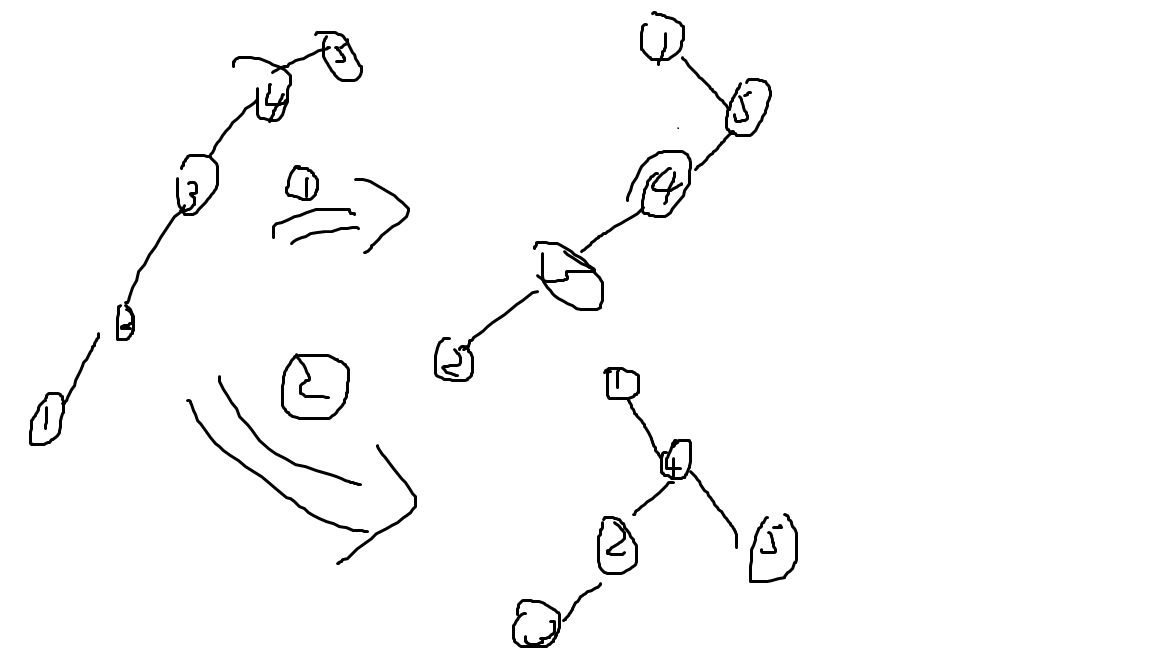
再放一张 zag-zig。

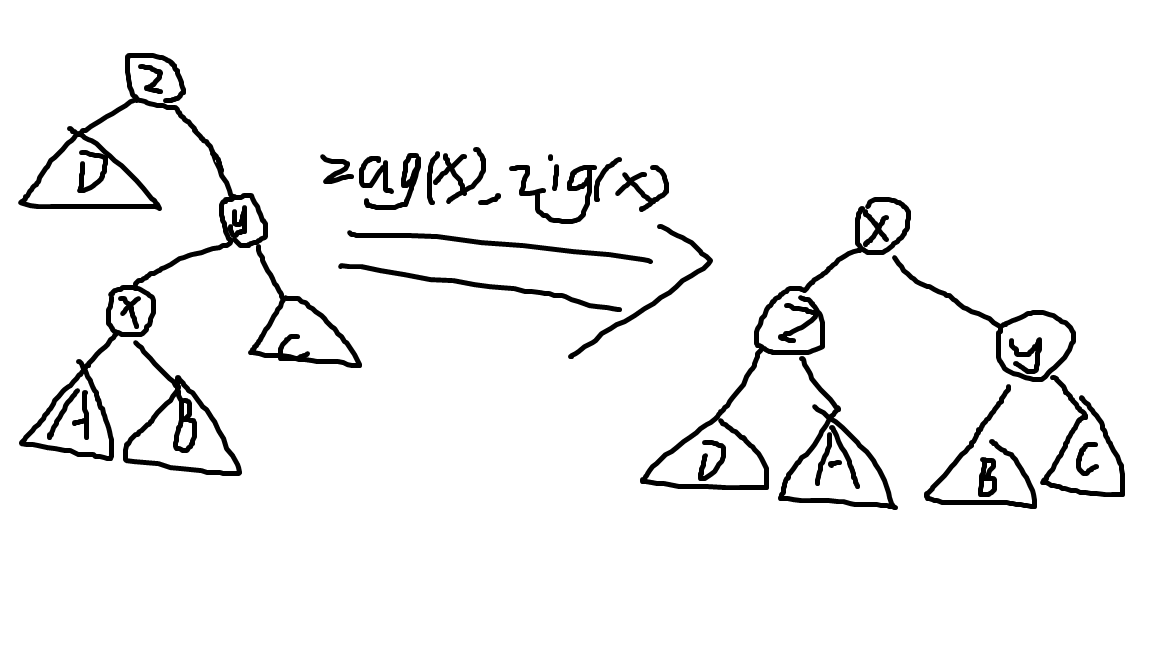
Q：为什么这里不先 zig(y) 了。
A：模拟发现先 zig(y) 后 \(x\) 的深度不会变，因为它被挂到 \(z\) 的右子树了。