线代杂谈

1.BEST 定理变式

现在需要求两点之间欧拉路径的数量。

首先，从普通 BEST 定理谈起。BEST 定理没有办法求不是欧拉图的图的欧拉回路数量（无法找到双射关系，会导致计算错误）。所以，计算时需要特判。

然后再考虑 BEST 定理求的欧拉回路的一些性质。

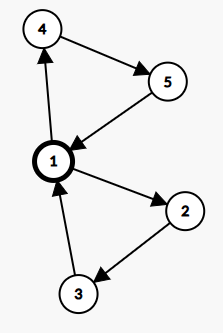
上面是一张简单得不能再简单的欧拉图。考虑这样两条欧拉回路。

\((1,4),(4,5),(5,1),(1,2),(2,3),(3,1)\)。
\((1,2),(2,3),(3,1),(1,4),(4,5),(5,1)\)。

很容易发现，这是在 BEST 定理中被称为循环同构的两条欧拉回路，所以会被算成 \(1\) 条。可以这样理解：由于不固定起点，并不能确定一条欧拉回路中哪条边是起点，哪条边是终点，只知道每条边的前驱后继关系。根据前驱后继关系来进行欧拉回路的区分，就自然有循环同构一说了。

但是，如果固定了起点，就要另当别论。洛谷 P5807 【模板】BEST 定理 | Which Dreamed It
就是如此。考虑固定起点后一条被认为是循环同构的路径能产生多少贡献。

\((1,2),(2,3),(3,1),(1,4),(4,5),(5,1)\)。

理论上来说，每一种循环移位都是一条新的路径，因为从起点开始先走的边不同一定对应不同的欧拉回路。但是这先走的边必须是起点的出边，所以只有 \(deg_s\) 的贡献。那么答案就是原 BEST 定理的答案乘上 \(deg_s\)。